Seven Segment Display Problem in Java

Seven segments display is an output display device. It provides a way to display information in the form of images, text, or decimal numbers. It is an alternative to complex dot matrix displays. Seven segment displays are widely used in digital or electronic devices like calculators, watches, game consoles, electronic meters, etc. In this section, we will discuss how to represent a number in seven-segment display in Java.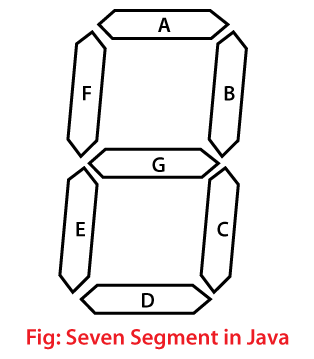

What is seven segment display?

It is a display device that forms a number using seven segments of LEDs (horizontal and vertical bars) that look like the number 8. These seven segments can form any number from 0 to 9. For example, consider the following figure.

Working of Seven Segment

The following table depicts the digits and corresponding segment code where 0 represents no power supply and 1 represents power supplied.

Digit	No. of Segment to Display a Number	Seven Segment Code
Digit	No. of Segment to Display a Number	a	b	C	d	e	f	g
0	6	1	1	1	1	1	1	0
1	2	0	1	1	0	0	0	0
2	5	1	1	0	1	1	0	1
3	5	1	1	1	1	0	0	1
4	4	0	1	1	0	0	1	1
5	5	1	0	1	1	0	1	1
6	6	1	0	1	1	1	1	1
7	3	1	1	1	0	0	0	0
8	7	1	1	1	1	1	1	1
9	6	1	1	1	0	0	1	1

We observe that the minimum number of segments to represent a digit is 2.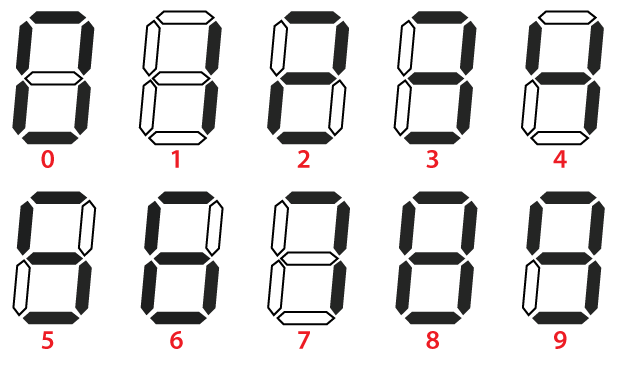

Before moving to the solution, first, we will see the Java program that displays the seven-segment digits.

Java Program to Represent a Digit in Seven Segment Form

There are the following two ways to print digits in seven-segment form:

Using switch case
Using Hexadecimal Encoding

Using switch Case

It is the naïve approach to print digit as seven segment display. In the following Java program, we have read a digit from the user and switched the corresponding case that prints the digit as seven segment display.

DisplaySevenSegment.java

import java.util.*;
public class DisplaySevenSegment
{
public static void main(String args[]) throws Exception 
{
Scanner sc = new Scanner(System.in);
System.out.print("Enter a digit you want to display: ");
//reads a digit from the user
int n = sc.nextInt();
//switch to the corresponding digit case
switch(n)
{
      case 0:
        System.out.println(" _ \n| | \n|_|");
        break;
      case 1:
        System.out.println("   \n  |\n  |");
        break;
      case 2:
        System.out.println(" _ \n _|\n|_ ");
        break;
      case 3:
        System.out.println(" _ \n _|\n _|");
        break;
      case 4:
        System.out.println("   \n|_|\n  |");
        break;
      case 5:
        System.out.println(" _ \n|_ \n _|");
        break;
      case 6:
        System.out.println(" _ \n|_ \n|_|");
        break;
      case 7:
        System.out.println(" _ \n  |\n  |");
        break;
      case 8:
        System.out.println(" _ \n|_|\n|_|");
        break;
      case 9:
        System.out.println(" _ \n|_|\n _|");
        break;
    }
  }
}

Output 1:

Let's see another way to print digits in seven segment display.

Using Hexadecimal Encoding

In the following Java program, we have used hexadecimal encoding to represent a digit in seven segment form. The following table depicts the same. In the table on represent, 1 and off represents 0.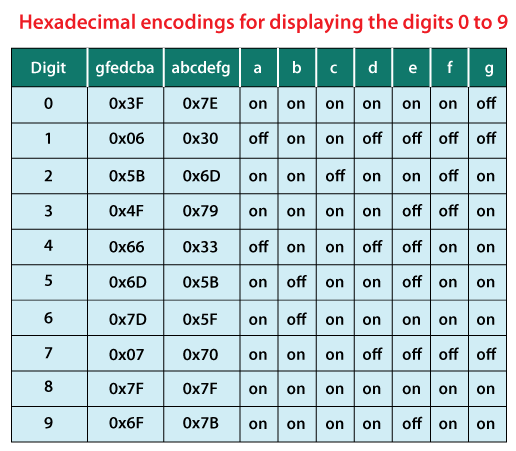

Let's implement the above logic in a Java program.

DisplayDigitSevenSegment.java

import 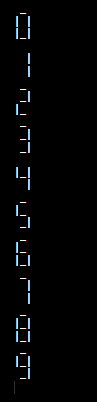java.util.HashMap;
import java.util.Map;
public class DisplayDigitSevenSegment 
{
private static final Map<Integer, Integer> encodings = new HashMap<Integer, Integer>();
//static block that stores key and corresponding values to the Map
//key-digit, value-hexadecimal encoding for displaying the digits 0 to 9 (in abcdefg sequence) 
static 
    {
        encodings.put(0, 0x7E);
        encodings.put(1, 0x30);
        encodings.put(2, 0x6D);
        encodings.put(3, 0x79);
        encodings.put(4, 0x33);
        encodings.put(5, 0x5B);
        encodings.put(6, 0x5F);
        encodings.put(7, 0x70);
        encodings.put(8, 0x7F);
        encodings.put(9, 0x7B);
    }
//driver code    
public static void main(String args[]) throws Exception 
    {
        //loop runs from 0 to 9 and print digits one by one by invoking the print method
        for (int i = 0; i < 10; i++) 
        {
            //calling the print method that prints the digit on the console
            printDigit(i);
        }
    }
//print method that computes how many segments are required to print a digit    
public static void printDigit(int digit) 
    {
        int code = encode(digit);
        char[] bits = String.format("%7s", Integer.toBinaryString(code)).replace(' ', '0').toCharArray();
        lightSegment(bits[0] == '1', " _ \n", "   \n");
        lightSegment(bits[5] == '1', "|", " ");
        lightSegment(bits[6] == '1', "_", " ");
        lightSegment(bits[1] == '1', "|\n", " \n");
        lightSegment(bits[4] == '1', "|", " ");
        lightSegment(bits[3] == '1', "_", " ");
        lightSegment(bits[2] == '1', "|\n", " \n");
    }
//the function decides which segment to be on or off
private static void lightSegment(boolean on, String onValue, String offValue) 
    {
        System.out.print(on ? onValue : offValue);
        try 
        {
            Thread.sleep(100);
        }
        catch (InterruptedException e) 
        {
            e.printStackTrace();
        }
    }
private static int encode(int digit) 
    {
        return encodings.containsKey(digit) ? encodings.get(digit) : 0x00;
    }
}

Output:

Problem Statement

The problem is divided into the following two subproblems.

In the first subproblem, we will compute the minimum number of segments required to display a number.
In the second subproblem, we will find the element that uses the minimum number of segments to display a number.

Let's discuss the subproblems one by one.

Subproblem 1

We have given an N-digit number and we have to find the minimum number of segments required to display each digit. Sum up all the segments and return the total number of segments to display the N-digit number.

Example:

Suppose, N=6 (number of digits) and s="234567".

The minimum number of segments requires to represent digit 2 is 5.

The minimum number of segments requires to represent digit 3 is 5.

The minimum number of segments requires to represent digit 4 is 4.

The minimum number of segments requires to represent digit 5 is 5.

The minimum number of segments requires to represent digit 6 is 6.

The minimum number of segments requires to represent digit 7 is 3.

So, the total number of segments that we require is 28 (5 + 5 + 4 + 5 + 6 + 3).

Let's implement the above approach in a Java program.

SegmentSum.java

public 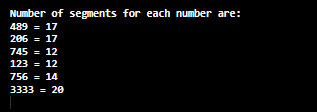class SegmentSum
{
//stored number of segments from 0 to 0
static int []seg = { 6, 2, 5, 5, 4, 5, 6, 3, 7, 6};
//return the number of segments used by x
static int computeSegment(int x)
{
if (x == 0)
return seg[0];
int count = 0;
//finding sum of the segment used by each digit of a number
while (x > 0)
{
count = count+seg[x % 10];
x = x/10;
}
//reyurns number of segments for each number
return count;
}
//driver program
static public void main (String args[])
{
int []arr = {489, 206, 745, 123, 756, 3333};
int n = arr.length;
System.out.println("Number of segments for each number are:");
//loop iterates over the array
for (int i=0; i<arr.length; i++)
{
System.out.println(arr[i]+" = "+computeSegment(arr[i])); 
}
}
}

Output:

Subproblem 2

In this problem, we have given an array of natural numbers. The task is to find which natural number uses the minimum number of segments to display a number. There might be a condition in which multiple natural numbers have the minimum number of segments, in such a case, the output will be the number that has the smallest index.

For example, consider the following array.

arr[] = {22, 46, 88, 12, 67, 90, 23, 55, 61}

22 -> 5+5 = 10

46 -> 4+6 = 10

88 -> 7+7 = 14

12 -> 2+5 = 7

67 -> 6+3 = 9

90 -> 6+6 = 12

23 -> 5+5 = 10

55 -> 5+5 = 10

61 -> 5+5 = 8

We observe that number 12 uses the minimum number of segments to display the number. So, the output will be 12.

Java Program to Find Element Using Minimum Segments in Seven Segments Display

In the following Java program, we have stored the number of segments of each digit. After that, we have defined the two functions one Computes segments for the digits and the second function computes the minimum segment for the entire number. After that, we have compared each digit's segments to each other and return the number that uses the minimum number of segments.

Let's see the Java program for the same.

SevenSegment.java

import java.io.*;
public class SevenSegment 
{
//precomputed values of segment used by digit 0 to 9
static int []seg = { 6, 2, 5, 5, 4, 5, 6, 3, 7, 6};
//return the number of segments used by x.
static int computeSegment(int x)
{
if (x == 0)
return seg[0];
int count = 0;
//finding sum of the segment used by each digit of a number
while (x > 0)
{
count = count + seg[x % 10];
x = x / 10;
}
return count;
}
static int elementMinSegment(int []arr, int n)
{
//initializing the minimum segment and minimum number index
int minseg = computeSegment(arr[0]);
int minindex = 0;
//finding and comparing segment used by each number arr[i]
for (int i = 1; i < n; i++)
{
int temp = computeSegment(arr[i]);
//if arr[i] used less segment then update the minimum segment and minimum number
if (temp < minseg)
{
minseg = temp;
minindex = i;
}
}
return arr[minindex];
}
//driver code
public static void main (String args[])
{
int []arr = {22, 46, 88, 12, 67, 90, 23, 55, 61};
//determines the length of the array
int n = arr.length;
//function calling
System.out.println(elementMinSegment(arr, n));
}
}

Output:

Complexity

The time complexity for the above approach is O(n * log₁₀n) and the space complexity is O(1).

Next TopicSplit Array Largest Sum in Java

← prev next →