Skew-symmetric matrixIn case of discrete mathematics, we can define a skew-symmetric matrix as a square matrix that is similar to the negation of its transpose matrix. We can call a matrix as square matrix if it contains the same number of rows and columns. If there is a matrix A, then the transpose of this matrix will be indicated by the symbol AT. If a matrix satisfies the condition A = -AT, then that matrix will be a skew-symmetric matrix. There are a lot of fields in which we can use the skew-symmetric matrix, like as statistical analysis, and in machine learning, and many more places. In this section, we will learn about skew-symmetric matrix, its definition, properties, theorems related to the skew-symmetric matrix, eigenvalue, a trace of skew-symmetric matrix, examples of skew-symmetric matrix and many more. What is Skew-symmetric matrixA matrix will be known as the skew-symmetric matrix if there is a square matrix which contains the same values in the negation of its transpose matrix. If we want to understand the concept of a skew-symmetric matrix, then we have to know about the method to determine the transpose of a matrix. Suppose there is a matrix B. We can determine the skew-symmetric matrix with the help of a formula, which is described as follows: B = -BT 
Transpose of a matrixA matrix will be known as the transpose matrix if we interchange the elements of rows or columns of the original matrix. We can indicate the transpose of a matrix with the help of symbol T. If there is a matrix which is indicated by n∗m, then its transpose matrix will be indicated by m∗n. Now we will understand the concept of transpose by an example, which is described as follows: For example: In this example, we have a 3∗3 matrix A. We will determine the transpose of matrix A. The elements of matrix A are described as follows: 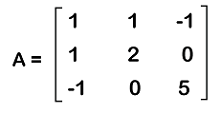
Solution: To perform the transpose of this matrix, we will change the first row into the first column and the second row will be changed into the second column, and the third row will be changed into the third column in the following way: 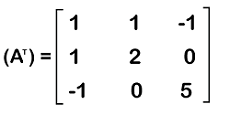
Here A = AT. Definition of Skew-symmetric matrixSuppose there is a square matrix B which contains the size n∗n. This matrix will be considered as symmetric iff BT = -B. If the negation of a skew-symmetric matrix and the transpose of that matrix are similar to each other, then we can call this matrix a skew-symmetric matrix. The skew-symmetric matrix can be represented in the following way: If there is a skew-symmetric matrix B = [bij]n∗n, then bij = -bji for all i and j or 1 ≤ i ≤ n and 1 ≤ j ≤ n. Here n is used to show any natural number. In this equation, if we put i = j, then we will get bii = 0 for all i. That means in this case of the skew-symmetric matrix, all the diagonal elements will be 0. Skew-symmetric matrix Example:Suppose there is a square matrix B, where 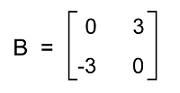
The transpose of this matrix is described as follows: 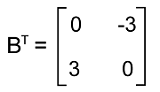
The negation of matrix B is described as follows: 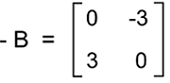
In this example, BT = -B, b12 = -b12 and b11 = b22 = 0. Hence we can say that matrix B is a skew-symmetric matrix. Steps to determine the Skew-symmetric matrixThere are some steps which we should be followed to determine whether the matrix is a skew-symmetric matrix or not, which are described as follows: Step 1: In the first step, we will determine the transpose of given matrix. Step 2: In the second step, we will determine the negation of given matrix. Step 3: In this step, we will see whether the transpose of the matrix and the negation of the matrix are similar to each other or not. Step 4: The matrix will be known as the skew-symmetric matrix if the transpose matrix and the negation of the matrix are similar to each other. Now we will understand all these steps by an example, which is described as follows: Suppose we have a matrix A where 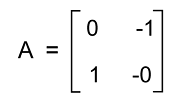
The transpose of this matrix is described as follows: 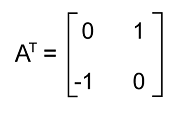
Now we will do the negation of matrix A and get the following: 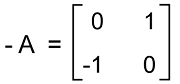
Here we can see that the transpose of matrix A and the negation of matrix A are similar to each other. Hence matrix A is a skew-symmetric matrix. Properties of Skew-symmetric matrixThere are two conditions which should be followed if we want to know whether the given matrix is a skew-symmetric matrix. According to the first condition, the given matrix must be a square matrix, i.e., it must have the same number of rows and columns. According to the second condition, the given matrix and the negation of its transpose must be similar to each other. There are various properties of a skew-symmetric matrix, and some of them are described as follows:
Theorems related to Skew-symmetric matricesIn case of skew-symmetric matrix, we have two important theorems. Here we will learn about both the theorems as well as their proofs. Theorem 1: If there is a square matrix B, which contains the real number elements, in this case, A + AT will be a symmetric matrix and A - AT will be a skew-symmetric matrix. Proof: Here we will assume that P = A + AT Now we will take the transpose of assumed matrix P and get the following: PT = (A + AT)T= AT+ (AT)T= AT+ A = A + AT= P This shows that A + AT is a symmetric matrix. After that, we will assume that Q = A - AT Now we will take the transpose of assumed matrix Q and get the following: QT = (A + (-AT))T= AT+ (-AT)T= AT- (AT)T= AT - A = -(A - AT) = -Q This shows that A - AT is a skew-symmetric matrix. Theorem 2: If there is a square matrix, then we can write this matrix as the addition of a symmetric matrix S and skew-symmetric matrix V. With the help of following formula, we can determine the addition of a skew-symmetric matrix and symmetric matrix. Suppose there is a square matrix B. Then, A = (1/2) × (A + AT) + (1/2) × (A - AT). Here AT is used to indicate the transpose of matrix A.
Hence if there is a square matrix, then we can write this matrix as the addition of a skew-symmetric matrix and symmetric matrix. Determinant of Skew-symmetric matrixNow we will use the following way to verify this property with the help of a 3∗3 matrix like this: 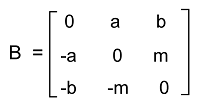
Now we will find the determinant of B with the help of following formula: |B| = 0 (cofactor of b11) + a (cofactor of b12) + b (cofactor of b13) = a (cofactor of b12) + b (cofactor of b13) = a((-1)1+2 (0 - (bm))) + b ((-1)1+3 (am)) = a(-1)3 (bm) + b (1)4 (am) = a(-1) (bm) + b (1) (am) = -abm + abm = 0 If there is a skew-symmetric matrix, which contains odd number of order, then the determinant of that matrix will always be zero. Eigen value of skew-symmetric matrixIn case of skew-symmetric matrix, the eigenvalues must either contain zero value or imaginary values. If there is a real skew-symmetric matrix A and real eigenvalue, in this case, λ will be equal to 0. It shows that we will get a non-real value if we have the nonzero eigenvalues in the skew-symmetric matrix. Proof: Suppose there is a square matrix indicated by A, an eigenvalue of A indicated by λ and an eigenvector corresponding to eigenvalue λ indicated by x. ⇒ Ax = λx Now we will use x̅T to multiply both sides of the above equation (here x̅T is used to indicate the conjugate of eigenvalue x) in the following way: x̅TAx = λ x̅Tx = λ||x||2 Here x̅TAx is used to indicate the dot product of x̅T and Ax. As we know that the dot product is commutative. So we will have the following: x̅TAx = (Ax)Tx̅ = xTATx̅. Here we have a skew-symmetric matrix A, so we will have AT = -A. Now we will put this value into the above equation and get the following: xTATx̅ = -xTAx̅ Now we will use the fact that A is real and take the conjugate of Ax = λx in the following way: Ax̅ =���λλ�x̅ Thus we will have the following: -xTAx̅ = -xT���λλ�x̅ = -���λλ�||x||2. -���λλ�||x||2= λ||x||2 Since there is an eigenvalue x and according to the definition, it is non-zero. Thus ||x|| ≠ 0. Hence we will have the following: -���λλ�= λ ⇒ λis either an imaginary number or zero. Trace of a Skew-symmetric matrixWe can calculate the trace of a matrix with the help of addition of all its diagonal elements. In case of skew-symmetric matrix, the elements of diagonal will always be 0. Because of this reason, the trace of this matrix will always be 0. Important Notes on Skew-symmetric matrixThere are some important points which we should know at the time of learning the concept of a skew-symmetric matrix. These points are described as follows:
Examples of Skew-symmetric matrixThere are a lot of examples of skew-symmetric matrices, and some of them are described as follows: Example 1: In this example, we have a matrix A, and we have to determine whether it is a skew-symmetric matrix. The elements of matrix A are described as follows: 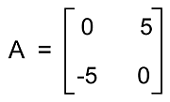
Solution: From the question, we have matrix A 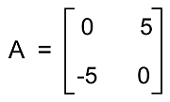
Now we will do the transpose of this matrix like this: 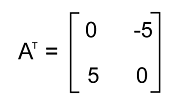
Now we will do the negation of matrix A like this: 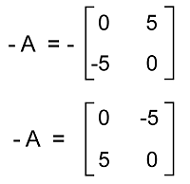
Here we have AT = -A, a12 = -a21 and a11 = a22 = 0. Answer: Matrix A is a skew-symmetric matrix. Example 2: In this example, we have a matrix A, and the elements of matrix A are described as follows: 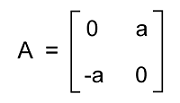
Here we have to determine which option is correct for matrix A.
Solution: The matrix A and its transpose are described as follows: 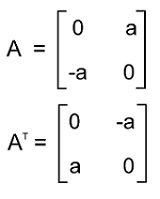
Now we will do the negation or inverse of original matrix A like this: 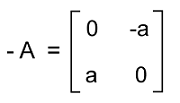
Here we can see that the transpose matrix AT and the inverse matrix (-A) are similar to each other. Here AT = -A, and a12 = -a21, and a11 = a22 = 0. Hence matrix A is a skew-symmetric matrix. Answer: The correct option is (a). Example 3: In this example, we have a skew-symmetric matrix A, where 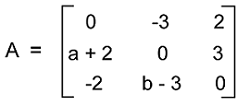
Now we have to determine the values of a and b. Solution: From the question, we know that A is a skew-symmetric matrix. So AT = -A. 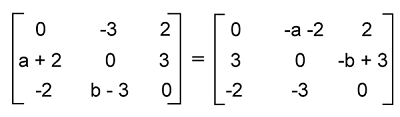
Now we will compare the corresponding elements in the following way: -a - 2 = -3 ⇒ -a = -1 ⇒ a = 1 -b + 3 = 3 ⇒ -b = 0 ⇒ b = 0 Answer: The value of a is 1, and the value of b is 0. Example 4: In this example, we have a matrix, and we have to determine whether the given matrix is a skew-symmetric matrix or not. 
Solution: Here, we will see whether matrix B is a skew-symmetric matrix or not. So for this, we will do the transpose of matrix B and the negation of matrix B. So we will first do the transpose of this matrix and get the following: 
Now we will do the negation or inverse of matrix B and get the following: 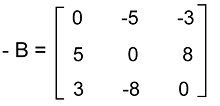
Here we can see that the transpose of matrix B and the negation of matrix B are similar to each other. Hence matrix B is a skew-symmetric matrix. Answer: Matrix B is a skew-symmetric matrix.
Next TopicSymmetric Matrix in Discrete mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










