Symmetric difference between two sets

In this article, we are going to discuss the symmetric difference between two sets. Here, we will also discuss the properties of symmetric difference between two sets.

Hope, this article will be helpful to you in order to understand the symmetric difference between two sets.

What is a Symmetric difference?

Another variant of difference is the symmetric difference. Suppose there are two sets, A and B. The symmetric difference between both sets A and B is the set that contains the elements that are present in both sets except the common elements.

The symmetric difference between two sets is also called as disjunctive union. Symmetric difference between two sets is a set of elements that are in both sets but not in their intersection. The symmetric difference between two sets A and B is represented by A Δ B or A ? B.

We can understand it via examples.

Example1 Suppose there are two sets with some elements.

Set A = {1, 2, 3, 4, 5}

Set B = {3, 5}

So, the symmetric difference between the given sets A and B is {1, 2, 4}

Or, we can say that A Δ B = {1, 2, 4}.

Example2 Suppose there are two sets with some elements.

Set A = {a, b, c, k, m, n}

Set B = {c, n}

So, the symmetric difference between the given sets A and B is {a, b, k, m}

Or, we can say that A Δ B = {a, b, k, m}.

In the below Venn diagram, you can see the symmetric difference between the two sets.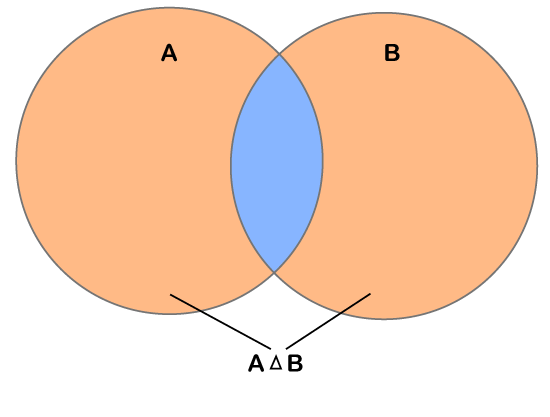

The part shaded with the skin color in the above Venn diagram is the symmetric difference between the given sets, i.e., A Δ B.

Let's see some of the properties of symmetric difference between two sets.

Properties

There are some of the properties of symmetric difference that are listed as follows;

The symmetric difference can be represented as the union of both relative complements, i.e.,
A Δ B = (A / B) ∪ (B / A)
The symmetric difference between two sets can also be expressed as the union of two sets minus the intersection between them -
A Δ B = (A ∪ B) - (A ∩ B)
The symmetric difference is commutative as well as associative -
A Δ B = B Δ A
(A Δ B) Δ C = A Δ (B Δ C)
The empty set is neutral (in mathematics, a neutral element is said to be a special type of element which, when combined with any element on the set to perform a binary operation, leaves the element unchanged. It is also known as the Identity element).
A Δ ∅ = A
A Δ A = ∅
If set A is equal to set B, then the symmetric difference between both sets is -
A Δ B = ∅ {when A = B}

'Symmetric difference between two sets' v/s 'Difference between two sets'

Difference between two sets

The difference between two sets A and B is a set of all those elements which belong to A but do not belong to B and is denoted by A - B.

Example: Let A = {1, 2, 3, 4}

and B = {3, 4, 5, 6}

then A - B = {3, 4} and B - A = {5, 6}

Symmetric difference between two sets

The symmetric difference between two sets, A and B, is the set containing all the elements that are in A or B but not in both. It is represented by A Δ B or A ? B.

Example: Let A = {1, 2, 3, 4}

and B = {3, 4, 5, 6}

then A Δ B = {1, 2, 5, 6}

Now, let's see some examples to understand the symmetric difference between two sets more clearly.

Question1 - Suppose you have the sets A = {10, 15, 17, 19, 20} and B = {15, 16, 18}. Find out the difference between both sets A and B and also find out the symmetric difference between them.

Solution - Given,

A = {10, 15, 17, 19, 20}

and B = {15, 16, 18}

Difference between both sets is -

A - B = {10, 15, 17, 19, 20} - {15, 16, 18}

= {10, 17, 19, 20}

Symmetric difference between both sets is -

A Δ B = {10, 15, 17, 19, 20} - {15, 16, 18}

= {10, 16, 17, 18, 19, 20}

Question2 - Suppose you have the sets A = {2, 4, 6, 8} and B = {2, 5, 7, 8}. Find out the symmetric difference B Δ A. Also, draw the Venn diagram to represent the symmetric difference between both given sets.

Solution - Given, A = {2, 4, 6, 8} and B = {2, 5, 7, 8}

We know that, B Δ A = (B ∪ A) - (B ∩ A)

Let's try to solve the question step by step. So, the first step is to find the union of set A and set B.

Therefore, (B ∪ A) = {2, 5, 7, 8} ∪ {2, 4, 6, 8}

= {2, 4, 5, 6, 7, 8}

After that, we have to calculate the intersection between both sets.

(B ∩ A) = {2, 5, 7, 8} ∩ {2, 4, 6, 8}

= {2, 8}

Now, we have to find the difference between the union and intersection of sets A and B, as stated in the formula,

So, (B ∪ A) - (B ∩ A) = {2, 4, 5, 6, 7, 8} - {2, 8}

= {4, 5, 6, 7}

Therefore, B Δ A = {4, 5, 6, 7}

Which will be equal to the A Δ B, as stated above, "Symmetric difference is commutative". Now, we will show the symmetric difference between both sets via the Venn diagram.

In the Venn diagram, first, we will draw two circles representing sets A and B. As calculated above, the intersection between both sets is {2, 8}, so we listed these elements in the intersecting region. Then, we list the remaining elements in their respective set circles, i.e. {4, 6} in set A and {5, 7} in set B. After arranging the elements, the Venn diagram will be -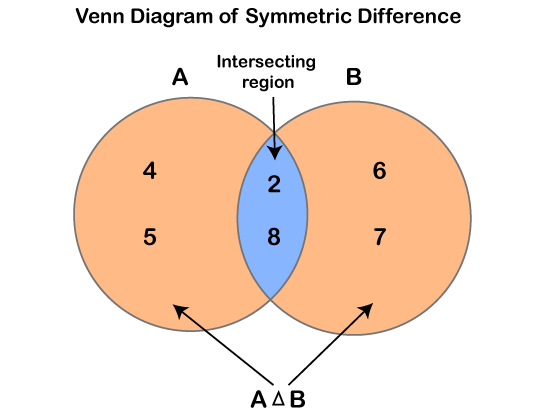

When we look at the above Venn diagram, there is a Universal set U. Both sets A and B are the subset of universal set U. Elements {2, 8} are the intersecting elements, so they are represented in the intersecting region. The region with light orange color is the union of sets except for the intersecting region. This region is the symmetric difference between both sets A and B, and will be represented as -

B Δ A = (B ∪ A) - (B ∩ A) = {4, 5, 6, 7}

Question 3 - Suppose you have the sets A = {5, 6, 8, 9, 10} and B = {2, 4, 7, 10, 19}.

Prove that the symmetric difference is commutative using the given sets.

Solution - Given, A = {5, 6, 8, 9, 10} and B = {2, 7, 8, 9, 10}

To prove: A Δ B = B Δ A

Take LHS,

A Δ B = (A ∪ B) - (A ∩ B)

(A ∪ B) = {5, 6, 8, 9, 10} ∪ (2, 7, 8, 9, 10}

= {2, 5, 6, 7, 8, 9, 10}

(A ∩ B) = {5, 6, 8, 9, 10} ∩ (2, 7, 8, 9, 10}

= {8, 9, 10}

So, A Δ B = {2, 5, 6, 7}