Symmetry Definition

If two additional identical pieces can be separated from a shape and arranged orderly, the structure has been defined to be symmetrical. For instance, when you are instructed to cut out a "heart" from a piece of paper, all you need to do is fold the sheet of paper, draw one-half of the heart at the fold, and then cut it out. Once you do this, you will discover that the other half coincides precisely with the first. The heart-shaped carving is an illustration of symmetry. Similarly, when a regular pentagon is divided, as in the illustration below, each half is symmetrical with respect to the other.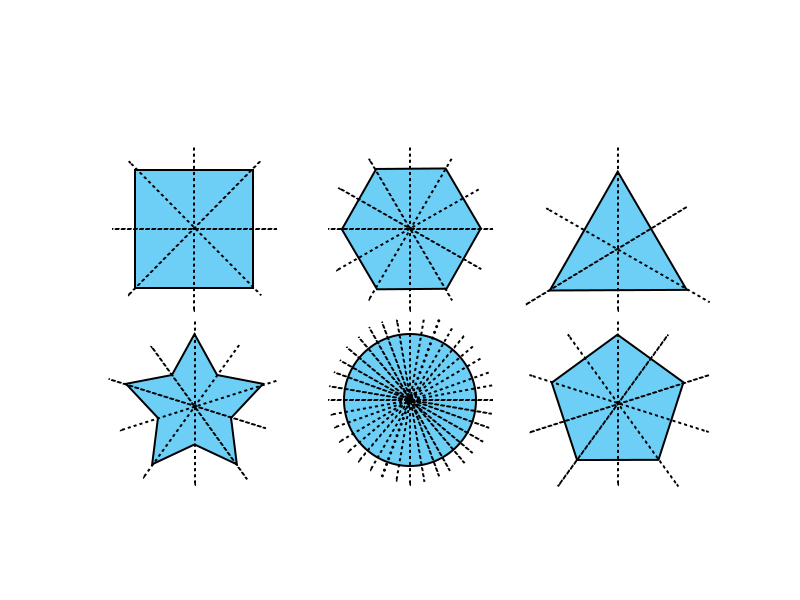

Aspects of Symmetry

Aspects of mathematical symmetry can be seen in abstract items like theoretical models, language, and music, as well as in the passage of time, as a spatial relationship, through geometric transformations, and in other functional transformations.

Symmetry has three different angles: mathematically, including geometry, which is the most well-known symmetry among readers; naturally; and artistically, including architecture, art, and music. Asymmetry, which denotes the lack of or a breach in symmetry, is the opposite of symmetry.

Symmetry in Mathematics

A geometric object or form is symmetric if it can be broken up into two or more identical pieces and then placed systematically. If a transformation changes specific parts of an item while maintaining the thing's overall shape, the object is said to be symmetric. The arrangement of the parts or the type of transformation determines the type of symmetry:

• Suppose a line (or, in 3D, a plane) passes through an item and divides it into two sections that are mirrored versions of one another. In that case, the object possesses reflectional symmetry (line or mirror symmetry).
• It has rotational symmetry if an item can be rotated around a fixed point (or in three dimensions, about a line) without affecting its general shape.
• It exhibits translational symmetry if an item can be translated (each point moved by the same amount) without affecting its general shape.
• If an item can be simultaneously translated & rotated in three dimensions around a line known as a screw axis, it possesses helical symmetry.
• If an object's shape remains the same as it is stretched or contracted, it possesses scale symmetry. Scale symmetry is another characteristic of fractals, wherein smaller fractal parts have a similar shape to more significant parts.
• Other symmetries include roto-reflection symmetry and glide reflection symmetry (a reflection followed by a translation).

A mathematical entity is symmetric with regard to a specific mathematical operation if, whenever applied to the object, this operation retains some property of the object, making inferences from geometrical symmetry in the preceding section. A group is formed by the assortment of actions maintaining a particular object's property.

In general, every type of mathematical structure has a unique form of symmetry. Calculus' even and odd functions, abstract algebra's symmetric groups, linear algebra's symmetric matrices, and Galois Theory's Galois groups are a few examples. As well as symmetric probability distributions and skewness?the asymmetries of distributions-symmetry also appears in statistics.

Line of Symmetry in Maths

An item can be divided into two identical parts along a line called a line of symmetry. We can fold this star into two equal parts because it is a star. A figure has two identical sides when folded in half along its symmetry axis. The axis of symmetry is the name given to this line of symmetry.

Based on its orientation, the line of symmetry falls into one of the following categories:

• Vertical Line
• Horizontal Line
• Diagonal line

Vertical line of symmetry

The horizontal line that splits a picture into two identical halves is a vertical line of symmetry. For instance, a standing straight line can divide the following shape into two identical halves. The symmetry line is vertical in such a scenario.

Horizontal line of symmetry

When a shape is split horizontally, i.e., from right to left or vice versa, the horizontal line of symmetry creates identical halves on each side. The following shape, for instance, can be divided into two identical halves when sliced horizontally. The symmetry line is horizontal in this instance.

Diagonal line of symmetry

When cut across the diagonal corners, a shape is divided into two identical halves by a diagonal line of symmetry. For instance, the following square shape can be divided into two identical halves by cutting across its corners. The symmetry line in this scenario is diagonal. An axis that divides an object into identical halves is known as a line of symmetry. There may be one, two, or more lines of symmetry in these items:

• One Symmetry Lines
• Two Symmetry Lines
• Infinity symmetry Lines

One symmetry line

One axis is the sole axis about which a figure has symmetry. It could be vertical, horizontal, or diagonal. For instance, the vertical line of symmetry running along the center of the letter "A" is one instance of symmetry.

Two symmetric lines

Only two lines are symmetrical in the figures with two lines of symmetry. The lines could be horizontal, vertical, or diagonal. For instance, the rectangle has both vertical and horizontal lines of symmetry.

Infinity symmetry lines

Only two lines are required for a figure to have infinite lines of symmetry. The lines could be horizontal, vertical, or diagonal. For instance, the rectangle has both vertical and horizontal lines of symmetry.

Types of Symmetry

When you flip, turn, or slide an object, symmetry can be seen. Four different types of symmetry can be seen:

• Translational symmetry
• Rotational symmetry
• Reflexive symmetry
• Glide symmetry

Translational symmetry

Translational symmetry is the process of moving an object from one point to another while maintaining its orientation in both forward and backward directions. In other words, the sliding of an object about an axis is what is meant by translation symmetry. For instance, the following figure illustrates translational symmetry, where the shape is moved both forward and backward while maintaining the same orientation and axis.

Rotational symmetry

Rotational symmetry, sometimes called radial symmetry, occurs when an item is rotated around a point in a specific direction. There is rotational symmetry when a form is rotated and remains the same as the origin. The order of symmetry describes how the item coincides with itself when it is in rotation. The rotational symmetry angle is the minimum angle at which the figure may be turned to coincide with itself.

Numerous geometrical shapes can represent rotational symmetry. For instance, figures like circles, squares, and rectangles show rotational symmetry. The starfish's structure may be seen to adhere to rotational symmetry in the image below. The starfish will continue to have the same appearance no matter how rotated or turned around; point P. Rotational symmetry can be seen in the well-known London Eye Ferris wheel. Numerous real-world objects, such as wheels, windmills, traffic signs, ceiling fans, and others, feature rotational symmetry.

Reflexive symmetry

A sort of symmetry known as reflective symmetry, sometimes known as mirror symmetry, occurs when one half of an item mirrors the other half. For instance, a human face's left and right sides are typically the same.

Glide symmetry

The result of combining translation and reflection transformations is glide symmetry. Since a glide reflection is commutative, the output is unaffected by changes to the combination's order.