Temperature Definition

A physical quantity known as temperature expresses the concepts of hotness and coldness in numerical form. With a thermometer, the temperature is measured. Thermometers are calibrated using a number of temperature scales that historically defined various reference points and thermometric substances. The most widely used scales are the Kelvin scale (K), which is primarily used for scientific purposes, the Fahrenheit scale (°F), and the Celsius scale (°C), formerly known as centigrade, with the unit symbol °C. In the International System of Units, one of the seven base units is the kelvin (SI).

The lowest point on the thermodynamic temperature scale is absolute zero, or zero Kelvin, or 273.15 °C. It can be very closely approached experimentally but never actually reached, as stated in the third law of thermodynamics. At that temperature, it would be impossible to produce heat from a body.

All areas of natural science, including physics, chemistry, Earth science, astronomy, biology, ecology, material science, metallurgy, mechanical engineering, geography, and most aspects of daily life, depending on temperature. These fields include medicine, biology, ecology, and most other branches of science.

Effects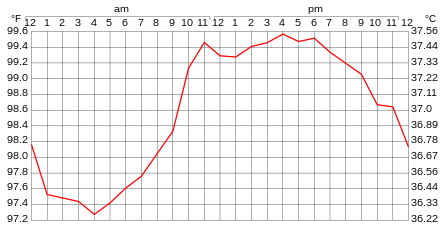

Human body temperature varies on average every day. The following are a few of the many physical processes that are connected to temperature:

• The physical characteristics of a material, such as its phase (solid, liquid, gaseous, or plasma), density, solubility, vapor pressure, electrical conductivity, hardness, wear resistance, thermal conductivity, corrosion resistance, and strength
• What happens to chemicals and how quickly and how much it happens
• Thermal radiation is emitted from an object's surface, including its intensity and composition.
• All living things are influenced by the air's temperature.
• The absolute temperature squared and the speed of sound, which in a gas is proportional.

Scales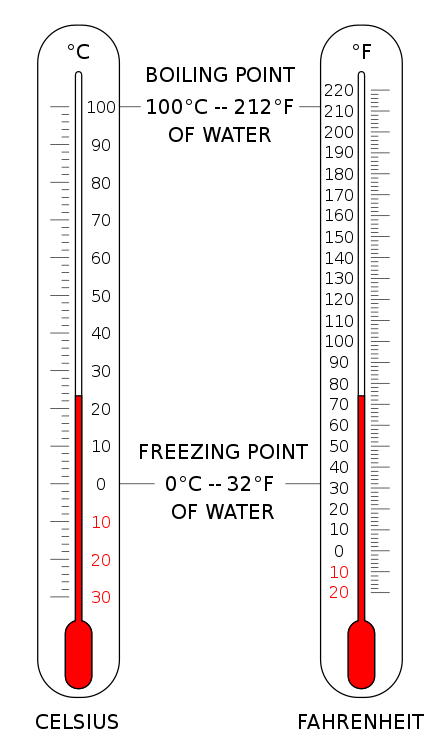

The point selected as zero degrees and the magnitudes of the incremental units of temperature is required for the definition of temperature scales. The Celsius scale (°C) is used for common temperature measurements in most of the world. It is an empirical scale that developed historically, which led to its zero point 0 °C being defined as the freezing point of water, and 100 °C as the boiling point of water, both at atmospheric pressure at sea level. It was called a centigrade scale because of the 100-degree interval.

Since the standardization of the kelvin in the International System of Units, it has subsequently been redefined in terms of the equivalent fixing points on the Kelvin scale, so that a temperature increment of one degree Celsius is the same as an increment of one kelvin, though numerically the scales differ by an exact offset of 273.15. In the US, people frequently use the Fahrenheit scale. At atmospheric pressure equal to that at sea level, water freezes at 32 °F and boils at 212 °F.

• Absolute Zero

At the absolute zero temperature, no energy can be removed from matter as heat, a fact expressed in the third law of thermodynamics. At this temperature, matter contains no macroscopic thermal energy but still has quantum-mechanical zero-point energy as predicted by the uncertainty principle, although this does not enter into the definition of absolute temperature.

Experimentally, absolute zero can only be reached after a very close approach (the lowest temperature attained by the experiment is 100 pK). Theoretically, all classical motion of the particles in a body at absolute zero temperature has ceased, and they are completely at rest in the classical sense. The exact value of absolute zero, denoted by the symbol 0 K, is 273.15 °C, or 459.67 °F.

• Absolute Scales

Referring to the Boltzmann constant, the Maxwell-Boltzmann distribution, and the Boltzmann statistical mechanical definition of entropy, as distinct from the Gibbs definition, for independently moving microscopic particles, disregarding interparticle potential energy, by international agreement, a temperature scale is defined and said to be absolute because it is independent of the characteristics of particular thermometric substances and thermometer mechanisms.

Apart from the absolute zero, it does not have a reference temperature. It is known as the Kelvin scale and is widely used in science and technology. The kelvin (the unit's name is spelled with a lowercase 'k') is the unit of temperature in the International System of Units (SI). The temperature of a body in a state of thermodynamic equilibrium is always positive relative to absolute zero.

In addition to the widely accepted Kelvin scale, Lord Kelvin also created a thermodynamic temperature scale with its numerical zero at absolute zero of temperature. This thermodynamic temperature scale is directly related to purely macroscopic thermodynamic concepts, such as macroscopic entropy, even though its microscopically equivalent is the Gibbs statistical mechanical definition of entropy for the canonical ensemble, which also takes into account interparticle potential energy. The numerical value of this scale's reference temperature at the triple point of water is determined by measurements made using the aforementioned, globally accepted Kelvin scale.

• Kelvin Scale

Many scientific measurements use the Kelvin temperature scale (unit symbol: K), named in honor of the physicist who first defined it. It is an absolute scale. It's numerical zero-point, 0 K, is at the absolute zero of temperature. Since May 2019, the kelvin has been defined through particle kinetic theory and statistical mechanics. In the International System of Units (SI), the magnitude of the kelvin is defined in terms of the Boltzmann constant, the value of which is defined as fixed by international convention.

Scale Classification

Different types of temperature scales exist. It might be useful to divide them into empirical and theoretically based categories. Historically speaking, empirical temperature scales predate theoretically based scales, which first appeared in the middle of the nineteenth century.

• Empirical Scales

Measurements of the basic macroscopic physical characteristics of materials serve as the foundation for empirically based temperature scales. For instance, the mercury-in-glass thermometer, which is incredibly useful, is built on the fact that the length of a mercury column, constrained in a glass-walled capillary tube, is greatly influenced by temperature. These scales are only useful for practical temperature ranges. For example, a mercury-in-glass thermometer is useless above the mercury's boiling point.

The majority of materials expand as the temperature rises, but some, like water, actually contract as the temperature rises over a narrow range, making them almost useless as thermometric materials. When a substance is close to one of its phase-change temperatures, like its boiling point, it is useless as a thermometer.

Despite these drawbacks, empirically based thermometers are the most widely used practical thermometers. It was used primarily for calorimetry, which made a significant contribution to the understanding of thermodynamics. However, when viewed as a foundation for theoretical physics, empirical thermometry suffers from significant shortcomings.

Empirically based thermometers can be re-calibrated by using theoretical physical reasoning, which can increase their range of suitability beyond their basic function as straightforward direct measurements of typical physical properties of thermometric materials.

• Theoretical Scales

Theoretical justifications, particularly those of kinetic theory and thermodynamics, serve as the foundation for theoretically based temperature scales. They are essentially idealized in physically workable materials and devices. Practical empirically based thermometers are calibrated using theoretically based temperature scales.

• The statistical mechanical scale at the microscopic level

The Kelvin scale is the name given to the commonly accepted conventional temperature scale in physics. The Boltzmann constant, which refers to the motions of microscopic particles like atoms, molecules, and electrons that are components of the body whose temperature is to be measured, is used to calibrate it. The current accepted Kelvin temperature is not determined by comparison with the temperature of a reference state of a standard body or in terms of macroscopic thermodynamics, in contrast to the thermodynamic temperature scale developed by Kelvin.

A body's Kelvin temperature, which is independent of its absolute zero temperature, is determined by measurements of a suitable subset of its physical characteristics, such as those with well-established theoretical justifications in terms of the Boltzmann constant. This constant alludes to specific types of microscopic particle motion within the structure of the body.

During those types of motion, the particles move independently of one another. Although inter-particle collisions frequently halt such motions, the motions are chosen for temperature measurement so that the non-interactive portions of their trajectories are known to be amenable to precise measurement in the intervals in between collisions. Interparticle potential energy is ignored for this purpose.

The Kelvin temperature is defined as being proportional to the average kinetic energy of microscopic particles that are not moving in an interactive manner and can be measured using the right methods in an ideal gas and other theoretically understood bodies. The Boltzmann constant is a straightforward multiple of the proportionality constant. When molecules, atoms, or electrons are released from a substance and their velocities are measured, the spectrum of their velocities frequently almost exactly follows a theoretical law known as the Maxwell-Boltzmann distribution, providing a reliable measurement of the temperatures for which the law is valid.

However, perhaps in the future, it will be possible to conduct successful experiments of this kind that directly use the Fermi-Dirac distribution for thermometry. Theoretically, one can determine the speed of sound in a gas based on the gas' molecular makeup, temperature, pressure, and Boltzmann constant value. This gives a relationship between temperature and the Boltzmann constant for a gas with known molecular makeup and pressure. The thermodynamic parameters that describe the state of a sample of water at its triple point cannot be known or measured with the same level of accuracy as those quantities.

A measurement of the speed of sound can therefore provide a more accurate measurement of the temperature of the gas when using the Boltzmann constant as the primary defined reference of exactly defined value. Due to Wien's displacement law, which has theoretical justification in Planck's law and the Bose-Einstein law, which states that the frequency of maximum spectral radiance of black-body radiation is directly proportional to the temperature of the black body, measurements of the electromagnetic radiation spectrum from an ideal three-dimensional black body can provide an accurate temperature measurement.

Accurate temperature measurement can also be achieved by measuring the power spectrum of electrical resistor noise. The resistor is essentially a one-dimensional body with two terminals. According to the Bose-Einstein law in this situation, the noise power is inversely correlated with the resistor's temperature, resistance value, and noise bandwidth. Johnson noise is the term for the noise power in a given frequency band that has equal contributions from all frequencies. The temperature can be determined if the resistance value is known.

• Macroscopic Thermodynamic Scale

Up until May 2019, the Kelvin scale was defined historically according to Kelvin's invention, which was based entirely on macroscopic thermodynamics and a ratio of energy quantities in the processes of a perfect Carnot engine. The temperature of the body whose temperature was to be measured and a reference temperature-that of a body at the triple point of water-were the two temperatures between which the Carnot engine was to operate.

The triple point was chosen as the reference temperature, and its exact value was determined to be 273.16 K. Since May 2019, that value has not been fixed by definition and must instead be determined through the aforementioned Boltzmann constant-related microscopic phenomena. The reference temperature for the microscopic statistical mechanical definition is not specified.

Ideal gas

The ideal gas is a substance on which a macroscopically defined temperature scale may be based. A fixed volume and mass of an ideal gas will exert a pressure that is directly proportional to its temperature. Some natural gases exhibit properties that are so close to being ideal at suitable temperatures that they can be used for thermometry. This was significant for the development of thermodynamics and is still relevant in today's world. However, there are some theoretical flaws with the ideal gas thermometer.

This is due to the fact that an ideal gas violates the third law of thermodynamics because its entropy at absolute zero temperature is not a positive semi-definite quantity. In contrast to real materials, the ideal gas does not liquefy or solidify, no matter how cold it is. Alternatively thinking, the ideal gas law, refers to the limit of infinitely high temperature and zero pressure; these conditions guarantee non-interactive motions of the constituent molecules.