Thermal Conductivity Definition

An indicator of a material's capacity to conduct heat is its thermal conductivity. It is commonly denoted by k, λ and κ. In contrast to materials with high thermal conductivity, low thermal conductivity materials transmit heat more slowly. For instance, insulating substances like Rockwool or polystyrene are effective at retaining heat while metals often have a high degree of thermal conductivity and are particularly effective at transferring heat.

In line with this, materials with high thermal conductivity are frequently used as heat sinks, whereas those with low thermal conductivity are employed as thermal insulation. Thermal resistance is the inverse of thermal conductivity.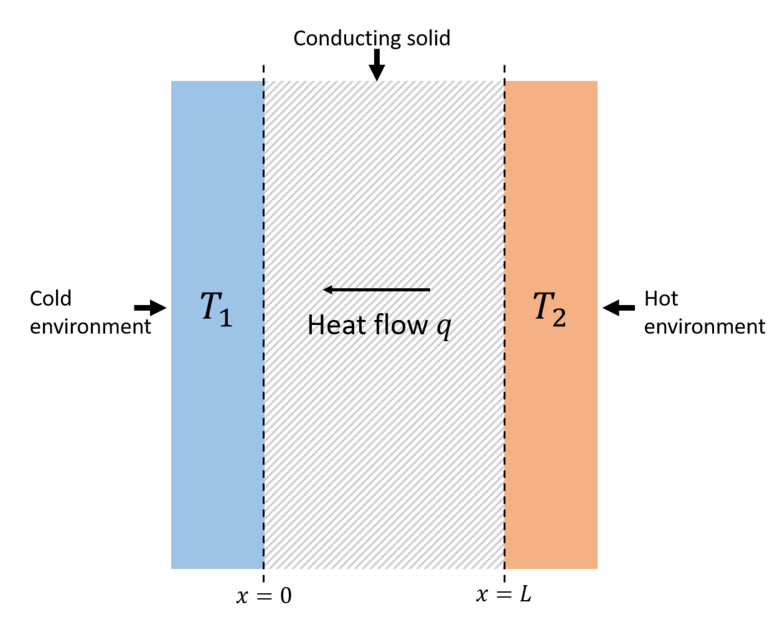

The formula of thermal conductivity is K = (QL) / (AΔT) . where

Q is the heat flux, k is the thermal conductivity, and ΔT is the temperature gradient. The term "Fourier's Law" for heat conduction refers to this. The most usual way to define thermal conductivity is as a scalar, but it can also take the shape of a second-rank tensor. Yet, anisotropic materials are the only ones where the tensorial description is required.

The second law of thermodynamics states that as temperature differences are diffused to equalise, heat will go from a hot environment to a cool one. Heat flux Q, which measures the rate at which heat moves in a certain direction per unit of area, is used to quantify this (in this case minus x-direction). In a lot of materials, it has been found that Q is inversely proportional to the separation distance L and directly proportional to the temperature difference.

Thermal conduction is the process by which energy is transported across a temperature difference as a result of random molecule motion. Because it does not include macroscopic flows or internal stressors that conduct work, it differs from energy transfer by convective and molecular work.

Units

The watts per metre-kelvin (W/(mK)) is the unit of measurement for thermal conductivity in the International System of Units (SI). Several articles express their findings in watts per centimeter-kelvin (W/(cmK)).

Thermal conductivity is calculated using BTU/(hft°F), which is used in imperial units.

Using the units of mass (M), length (L), time (T), and temperature (), we can write the dimension of thermal conductivity as M1L1T31.

The construction and textile industries frequently employ other measurements that are closely linked to thermal conductivity. The R-value (resistance) and U-value are two metrics used in the building business (transmittance or conductance). R- and U-values are measured per unit area and depend on the stated thickness of the product or assembly, even though they are linked to the thermal conductivity of a material employed in an insulation product or assembly. Similar to how R-values are used in the building sector, the textile industry also uses a number of units, such as the tog and clo, to indicate a material's thermal resistance.

Measurement

Thermal conductivity can be measured in a number of ways, but each is only appropriate for a certain class of materials. In general, there are two types of measurement methods: steady-state and transient. Transient procedures work on the instantaneous state of a system on the approach to a steady state, whereas steady-state methods infer the thermal conductivity from data on the state of a substance once a steady-state ambient temperature has been established.

Steady-state methods do not necessitate intricate signal analysis since they lack an obvious time component (steady state implies constant signals). The drawback is that in most cases, a well-engineered experimental apparatus is necessary, and quick measurement is not possible because of the time needed to attain steady state.

Fluids are more challenging to analyse experimentally in terms of their thermal properties than solid materials are. This is due to the fact that, unless steps are taken to inhibit these processes, convection and radiative heat transport are also frequently present in parallel to thermal conduction. It is also possible for the thermal conductivity to appear to decrease as an insulating boundary layer forms.

Experimental Results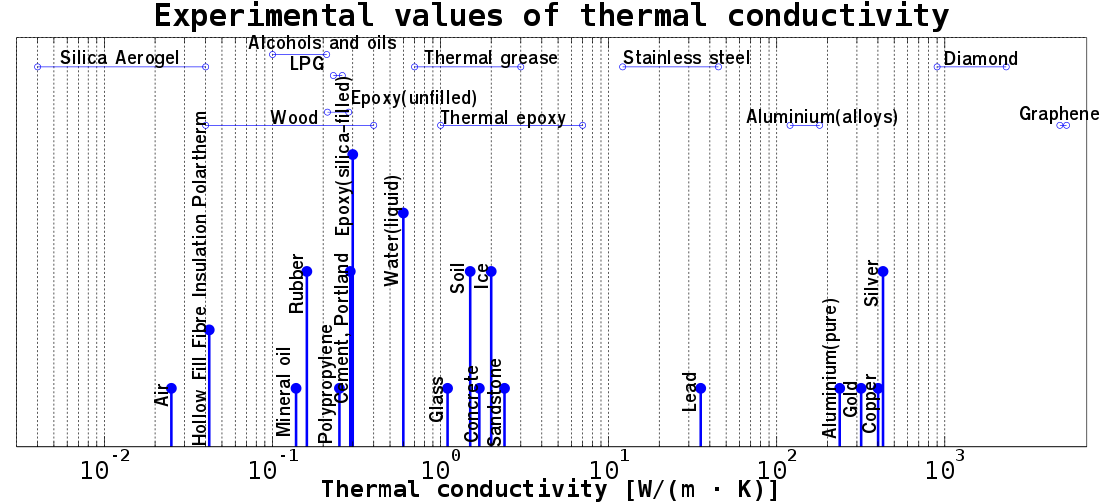

Common compounds have thermal conductivities that range by at minimum four orders of magnitude. In general, pure metals have a high thermal conductivity compared to gases, which are often low. The heat conductivity of copper, for instance, is more than 10,000 times greater than that of air under normal circumstances.

Carbon allotropes like graphite and diamond are frequently cited as having the greatest thermal conductivities of all materials at room temperature. A highly conductive metal like copper cannot compare to the thermal conductivity of a natural diamond at normal temperature, which is many times higher (although the precise value varies depending on the diamond type).

The thermal conductivities of a few selected materials are tabulated here; an expanded list may be found in the list of thermal conductivities. These figures are simply estimations meant to serve as examples because they don't take measurement ambiguities or variations in material specifications into consideration.

Influential Variables

• Temperature

For metals and nonmetals, the relationship between temperature and thermal conductivity is not the same. The main reason why metals conduct heat is because of free electrons. According to the Wiedemann-Franz law, the absolute temperature (in kelvins) multiplied by the electrical conductivity is roughly proportional to the metal's thermal conductivity. The thermal conductivity, which is the product of the electrical conductivity and temperature, is roughly constant in pure metals since the electrical conductivity declines with temperature.

However, the thermal conductivity rapidly drops when temperatures get close to zero degrees. The change in electrical conductivity is typically less pronounced in alloys, and as a result, thermal conductivity rises with temperature, frequently proportionately. The peak thermal conductivity of many pure metals is between 2 and 10 K.

On the other hand, lattice vibrations are primarily responsible for the heat conductivity of nonmetals (phonons). The phonon means free path is not greatly diminished with increasing temperatures, with the exception of high-quality crystals at low temperatures. As a result, at high temperatures, the thermal conductivity of nonmetals remains roughly constant. Thermal conductivity and heat capacity both decline at low temperatures much below the Debye temperature as a result of carrier scattering from imperfections.

• Physical State

The thermal conductivity of a substance may alter suddenly as it goes through a phase change (for example, from solid to liquid). For instance, the thermal conductivity decreases from 2.18 W/(mK) to 0.56 W/(mK) as the ice melts to become liquid water at 0 °C. The thermal conductivity of a fluid diverges even more noticeably close to the vapor-liquid critical point.

• Anisotropy In The Heat

Different thermal conductivities can be seen in some materials, such as non-cubic crystals, depending on the crystal axes. With thermal conductivities of 35 W/(mK) along the c axis and 32 W/(mK) along the axis, sapphire is a prominent example of a material with varying thermal conductivity based on orientation and temperature. The grain of wood often conducts better than the cross grain.

The materials used for the Space Shuttle thermal protection system, laminated materials, cables, metals that have undergone extensive cold pressing, and fiber-reinforced composite constructions are a few other examples of materials whose thermal conductivity varies with direction. The flow of heat may not follow the same path as the thermal gradient when anisotropy is present.

• Conductive Electricity

According to the Wiedemann-Franz law, thermal conductivity and electrical conductivity are roughly connected in metals because freely moving valence electrons can transport both heat and electricity. Because phonon carriers play a greater role in the transfer of heat in non-metals, the usual association among electrical and thermal conductance does not apply to other materials. In comparison to diamond, which is an electrical insulator but conducts heat through phonons because of its ordered atom arrangement, highly electrical conductor silver is less thermally conductive.

• Field of Magnetism

The thermal Hall effect, also known as the Righi-Leduc effect, is the name given to the effect of magnetic fields on thermal conductivity.

• The Phases of Gas

Air and other gases function well as insulators when convection is absent. Hence, a lot of insulating materials only work by having plenty of gas-filled pockets that block the flow of heat. Warm clothing as well as expanded and extruded polystyrene, more often known as "styrofoam," and silica aerogel are examples of these. Similar results are obtained by trapping air in pores, pockets, or voids in natural, biological insulators like fur and feathers.

The thermal conductivity of low density gases like hydrogen and helium is often high. The thermal conductivity of dense gases is low, such as that of xenon and dichlorodifluoromethane. Because of its large heat capacity, the dense gas sulphur hexafluoride is an exception and has a comparatively high thermal conductivity. Gases denser than air, such as argon and krypton, are frequently employed in double-paned windows with insulated glass to enhance their insulating properties.

• Atomic Purity

If other lattice flaws are minimal, a crystal's isotopic purity can have a significant impact on its heat conductivity. A famous example is diamond, whose thermal conductivity rises at temperatures around 100 K from 10,000 Wm1K1 for naturally occurring type IIa diamonds (98.9% 12C) to 41,000 Wm1K1 for artificially enriched diamonds that are 99.9%. Under the assumption that the crystal is otherwise pure, a value of 200,000 is expected for 99.999% 12C at 80 K. It is 90% more thermally conductive than natural boron nitride, with 99% isotopically enriched cubic boron nitride having a thermal conductivity of 1400 Wm1K1.

• Prediction

A finite number of experimental measurements cannot completely quantify thermal conductivity because it depends continually on factors such as temperature and material composition. If experimental values are unavailable for the relevant physical circumstances, predictive formulas are required. This capacity is crucial for thermophysical simulations because it allows for the inclusion of extreme conditions that are not accessible for direct measurement and where variables like temperature and pressure vary constantly with both space and time.