Threaded Binary Tree

In this article, we will understand about the threaded binary tree in detail.

What do you mean by Threaded Binary Tree?

In the linked representation of binary trees, more than one half of the link fields contain NULL values which results in wastage of storage space. If a binary tree consists of n nodes then n+1 link fields contain NULL values. So in order to effectively manage the space, a method was devised by Perlis and Thornton in which the NULL links are replaced with special links known as threads. Such binary trees with threads are known as threaded binary trees. Each node in a threaded binary tree either contains a link to its child node or thread to other nodes in the tree.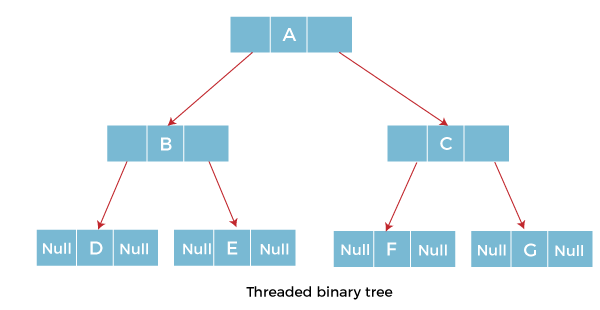

Types of Threaded Binary Tree

There are two types of threaded Binary Tree:

One-way threaded Binary Tree
T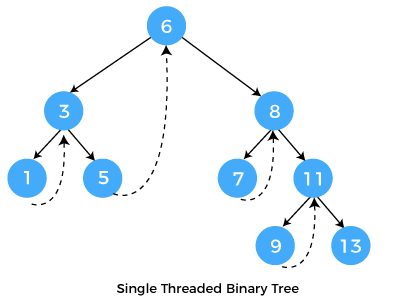wo-way threaded Binary Tree

One-way threaded Binary trees:

In one-way threaded binary trees, a thread will appear either in the right or left link field of a node. If it appears in the right link field of a node then it will point to the next node that will appear on performing in order traversal. Such trees are called Right threaded binary trees. If thread appears in the left field of a node then it will point to the nodes inorder predecessor. Such trees are called Left threaded binary trees. Left threaded binary trees are used less often as they don't yield the last advantages of right threaded binary trees. In one-way threaded binary trees, the right link field of last node and left link field of first node contains a NULL. In order to distinguish threads from normal links they are represented by dotted lines.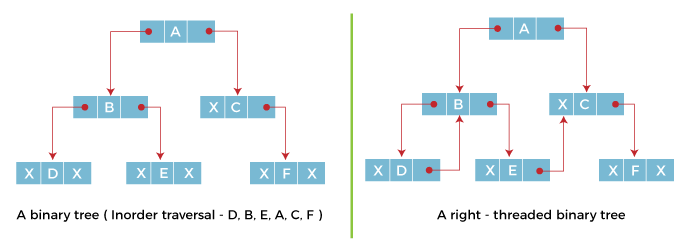

The above figure shows the inorder traversal of this binary tree yields D, B, E, A, C, F. When this tree is represented as a right threaded binary tree, the right link field of leaf node D which contains a NULL value is replaced with a thread that points to node B which is the inorder successor of a node D. In the same way other nodes containing values in the right link field will contain NULL value.

Two-way threaded Binary Trees: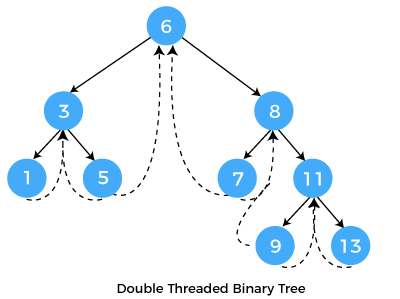

In two-way threaded Binary trees, the right link field of a node containing NULL values is replaced by a thread that points to nodes inorder successor and left field of a node containing NULL values is replaced by a thread that points to nodes inorder predecessor.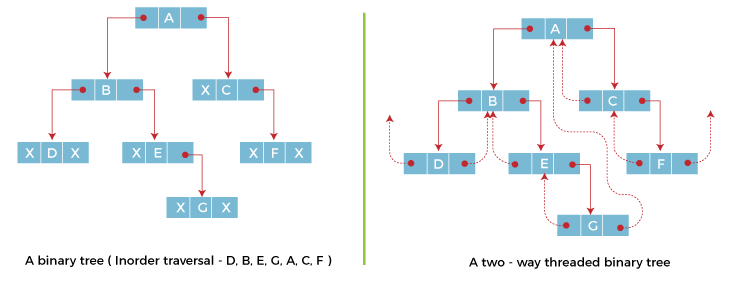

The above figure shows the inorder traversal of this binary tree yields D, B, E, G, A, C, F. If we consider the two-way threaded Binary tree, the node E whose left field contains NULL is replaced by a thread pointing to its inorder predecessor i.e. node B. Similarly, for node G whose right and left linked fields contain NULL values are replaced by threads such that right link field points to its inorder successor and left link field points to its inorder predecessor. In the same way, other nodes containing NULL values in their link fields are filled with threads.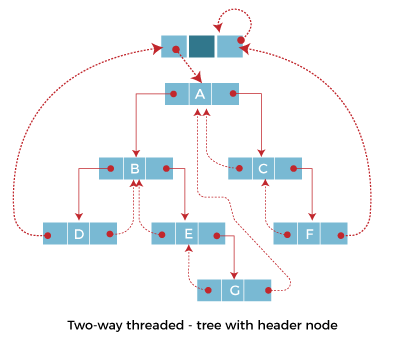

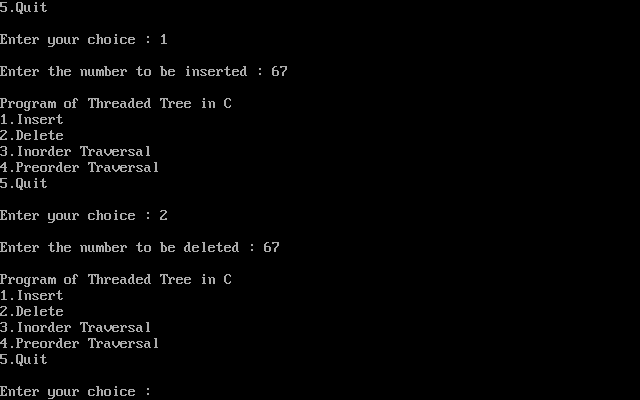
In the above figure of two-way threaded Binary tree, we noticed that no left thread is possible for the first node and no right thread is possible for the last node. This is because they don't have any inorder predecessor and successor respectively. This is indicated by threads pointing nowhere. So in order to maintain the uniformity of threads, we maintain a special node called the header node. The header node does not contain any data part and its left link field points to the root node and its right link field points to itself. If this header node is included in the two-way threaded Binary tree then this node becomes the inorder predecessor of the first node and inorder successor of the last node. Now threads of left link fields of the first node and right link fields of the last node will point to the header node.

Algorithm for Inorder Traversal of Threaded Binary Tree:

ALgorithm Inorder(I)
{
  ThreadedTreeNode *Header;
  Header=I;
  while(1)
  {
    I=fnFindInorder_Successor(H);
    if(I==Header)
     return;
    else
     print(I->info);
   }
}  
In the above algorithm, we have discussed the Inorder traversal of Threaded binary trees. 
Pseudocode of Threaded Tree in C:
#include <stdio.h>
#include <stdlib.h>
typedef enum {false,true} boolean;
struct node *in_succ(struct node *p);
struct node *in_pred(struct node *p);
struct node *insert(struct node *root, int ikey);
struct node *del(struct node *root, int dkey);
struct node *case_a(struct node *root, struct node *par,struct node *ptr);
struct node *case_b(struct node *root,struct node *par,struct node *ptr);
struct node *case_c(struct node *root, struct node *par,struct node *ptr);
void inorder( struct node *root);
void preorder( struct node *root);

struct node
{
        struct node *left;
        boolean lthread;
        int info;
        boolean rthread;
        struct node *right;
};
int main( )
{
clrscr();
	int choice,num;
        struct node *root=NULL;
        while(1)
        {
	       printf("\Program of Threaded Tree in C\n");
                printf("1.Insert\n");
                printf("2.Delete\n");
                printf("3.Inorder Traversal\n");
                printf("4.Preorder Traversal\n");
                printf("5.Quit\n");
                printf("\nEnter your choice : ");
                scanf("%d",&choice);
                switch(choice)
                {
                 case 1:
                        printf("\nEnter the number to be inserted : ");
                        scanf("%d",&num);
                        root = insert(root,num);
                        break;
                 case 2:
                        printf("\nEnter the number to be deleted : ");
                        scanf("%d",&num);
                        root = del(root,num);
                        break;
                 case 3:
                        inorder(root);
                        break;
                 case 4:
                        preorder(root);
                        break;
                 case 5:
                         exit(1);

                 default:
                        printf("\nWrong choice\n");
		}
	}
        return 0;
}
struct node *insert(struct node *root, int ikey)
{
	struct node *tmp,*par,*ptr;
	int found=0;
	ptr = root;
	par = NULL;
	while( ptr!=NULL )
	{
		if( ikey == ptr->info)
		{
			found =1;
			break;
		}
		par = ptr;
		if(ikey < ptr->info)
		{
			if(ptr->lthread == false)
				ptr = ptr->left;
			else
				break;
		}
		else
		{
			if(ptr->rthread == false)
				ptr = ptr->right;
			else
				break;
		}
	}
	if(found)
		printf("\nDuplicate key");
	else
	{
		tmp=(struct node *)malloc(sizeof(struct node));
		tmp->info=ikey;
		tmp->lthread = true;
		tmp->rthread = true;
		if(par==NULL)
		{
			root=tmp;
			tmp->left=NULL;
			tmp->right=NULL;
		}
		else if( ikey < par->info )
		{
			tmp->left=par->left;
			tmp->right=par;
			par->lthread=false;
			par->left=tmp;
		}
		else
		{
			tmp->left=par;
			tmp->right=par->right;
			par->rthread=false;
			par->right=tmp;
		}
	}
	return root;
}

struct node *del(struct node *root, int dkey)
{
	struct node *par,*ptr;
	int found=0;
	ptr = root;
	par = NULL;
	while( ptr!=NULL)
	{
		if( dkey == ptr->info)
		{
			found =1;
			break;
		}
		par = ptr;
		if(dkey < ptr->info)
		{
			if(ptr->lthread == false)
				ptr = ptr->left;
			else
				break;
		}
		else
		{
			if(ptr->rthread == false)
				ptr = ptr->right;
			else
				break;
		}
	}
	if(found==0)
		printf("\ndkey not present in tree");
	else if(ptr->lthread==false && ptr->rthread==false)/*2 children*/
		root = case_c(root,par,ptr);
	else if(ptr->lthread==false )
	root = case_b(root, par,ptr);
	else if(ptr->rthread==false)
	root = case_b(root, par,ptr);
	else
		root = case_a(root,par,ptr);
	return root;
}

struct node *case_a(struct node *root, struct node *par,struct node *ptr )
{
	if(par==NULL)
		root=NULL;
	else if(ptr==par->left)
	{
		par->lthread=true;
		par->left=ptr->left;
	}
	else
	{
		par->rthread=true;
		par->right=ptr->right;
	}
	free(ptr);
	return root;
}
struct node *case_b(struct node *root,struct node *par,struct node *ptr)
{
	struct node *child,*s,*p;
	if(ptr->lthread==false)
		child=ptr->left;
	else
		child=ptr->right;
        if(par==NULL )   
                root=child;
        else if( ptr==par->left) 
                par->left=child;
        else                     
                par->right=child;
        s=in_succ(ptr);
        p=in_pred(ptr);
        if(ptr->lthread==false) 
                        p->right=s;
        else
        {
		if(ptr->rthread==false) 
                        s->left=p;
        }
        free(ptr);
        return root;
} 
struct node *case_c(struct node *root, struct node *par,struct node *ptr)
{
        struct node *succ,*parsucc;
        parsucc = ptr;
        succ = ptr->right;
        while(succ->left!=NULL)
        {
                parsucc = succ;
                succ = succ->left;
        }
        ptr->info = succ->info;
        if(succ->lthread==true && succ->rthread==true)
                root = case_a(root, parsucc,succ);
        else
                root = case_b(root, parsucc,succ);
        return root;
}
struct node *in_succ(struct node *ptr)
{
        if(ptr->rthread==true)
                return ptr->right;
        else
        {
                ptr=ptr->right;
                while(ptr->lthread==false)
                        ptr=ptr->left;
                return ptr;
        }
} 
struct node *in_pred(struct node *ptr)
{
        if(ptr->lthread==true)
                return ptr->left;
        else
        {
                ptr=ptr->left;
                while(ptr->rthread==false)
                        ptr=ptr->right;
                return ptr;
        }
}
void inorder( struct node *root)
{
        struct node *ptr;
        if(root == NULL )
        {
                printf("Tree is empty");
                return;
        }
        ptr=root;
        while(ptr->lthread==false)
                ptr=ptr->left;
        while( ptr!=NULL )
        {
                printf("%d ",ptr->info);
                ptr=in_succ(ptr);
        }
}
void preorder(struct node *root )
{
        struct node *ptr;
        if(root==NULL)
        {
                printf("Tree is empty");
                return;
        }
        ptr=root;
        while(ptr!=NULL)
        {
                printf("%d ",ptr->info);
                if(ptr->lthread==false)
                        ptr=ptr->left;
                else if(ptr->rthread==false)
                        ptr=ptr->right;
                else
                {
                        while(ptr!=NULL && ptr->rthread==true)
                                ptr=ptr->right;
                        if(ptr!=NULL)
                                ptr=ptr->right;
                }
        }
}

Explanation:

In the above example, we have created a threaded binary tree for various operations.

Output: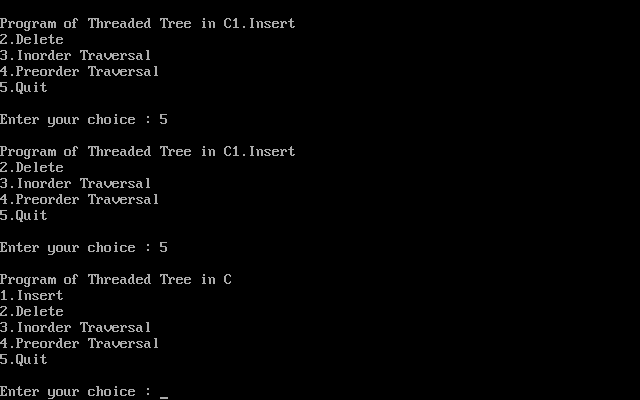

Advantages of Threaded Binary Tree:

In threaded binary tree, linear and fast traversal of nodes in the tree so there is no requirement of stack. If the stack is used then it consumes a lot of memory and time.
It is more general as one can efficiently determine the successor and predecessor of any node by simply following the thread and links. It almost behaves like a circular linked list.

Disadvantages of Threaded Binary Tree:

When implemented, the threaded binary tree needs to maintain the extra information for each node to indicate whether the link field of each node points to an ordinary node or the node's successor and predecessor.
Insertion into and deletion from a threaded binary tree are more time consuming since both threads and ordinary links need to be maintained.

Next TopicDiameter of Binary Tree

← prev next →