Torque-Slip and Torque-Speed CharacteristicsThe Torque-slip curve of an induction motor shows the variation of torque with the slip. We have
If R2 and X20 are kept constant, then the torque τ will depend upon the slip s. The torque-slip characteristic curve is divided into three regions:
(a) Low-slip regionAt synchronous speed s = 0, the torque will be zero. When the speed is very near to synchronous speed, the slip is very low and (sX20)2 is negligible in comparison with R2. Therefore,
When k2 = k1/R2 From the above relation, we can see that the torque is proportional to the slip. Hence, when the slip is small, the torque-slip curve is a straight line. (b) Medium-slip regionAs slip increases, the term (sX20)2 becomes large, so that Thus, the torque is inversely proportional to slip towards standstill conditions. We can represent the torque-slip characteristic by a rectangular hyperbola. For intermediate values of the slip, the graph changes from one form to another. In doing so, it passes through the point of maximum torque when R2 = sX20. The maximum torque developed in an induction motor is called the pull-out torque or breakdown torque. This developed torque is a measure of the short-time overloading capability of the motor. (c) High-slip regionThe torque decreases beyond the point of maximum torque, and the result is that the motor slows down and then stops. At this stage, we should immediately disconnect the motor from the supply to prevent the damage due to overloading. The motor operates for the value of the slip between s=0 and s = sM, where sM is the value of the slip corresponding to maximum torque. For a typical induction motor, the pull-out torque is 2 to 3 times the rated full-load torque. Thus, the motor can handle short- time overload, without stalling. The starting torque is 1.5 times the rated full-load torque. The figure drawn below shows the torque-slip curves and torque-speed curves: 
Figure: Torque-slip Curves 
Figure: Torque-speed Curves
Next Topic#
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





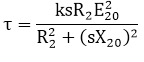
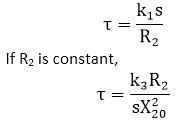
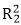 may be neglected in comparison with (sX20)2 and
may be neglected in comparison with (sX20)2 and




