Tree traversal (Inorder, Preorder an Postorder)

In this article, we will discuss the tree traversal in the data structure. The term 'tree traversal' means traversing or visiting each node of a tree. There is a single way to traverse the linear data structure such as linked list, queue, and stack. Whereas, there are multiple ways to traverse a tree that are listed as follows -

Preorder traversal
Inorder traversal
Postorder traversal

So, in this article, we will discuss the above-listed techniques of traversing a tree. Now, let's start discussing the ways of tree traversal.

Preorder traversal

This technique follows the 'root left right' policy. It means that, first root node is visited after that the left subtree is traversed recursively, and finally, right subtree is recursively traversed. As the root node is traversed before (or pre) the left and right subtree, it is called preorder traversal.

So, in a preorder traversal, each node is visited before both of its subtrees.

The applications of preorder traversal include -

It is used to create a copy of the tree.
It can also be used to get the prefix expression of an expression tree.

Algorithm

Until all nodes of the tree are not visited

Step 1 - Visit the root node
Step 2 - Traverse the left subtree recursively.
Step 3 - Traverse the right subtree recursively. 

Example

Now, let's see the example of the preorder traversal technique.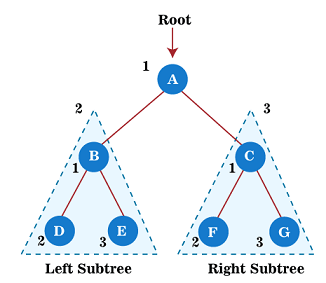

Now, start applying the preorder traversal on the above tree. First, we traverse the root node A; after that, move to its left subtree B, which will also be traversed in preorder.

So, for left subtree B, first, the root node B is traversed itself; after that, its left subtree D is traversed. Since node D does not have any children, move to right subtree E. As node E also does not have any children, the traversal of the left subtree of root node A is completed.

Now, move towards the right subtree of root node A that is C. So, for right subtree C, first the root node C has traversed itself; after that, its left subtree F is traversed. Since node F does not have any children, move to the right subtree G. As node G also does not have any children, traversal of the right subtree of root node A is completed.

Therefore, all the nodes of the tree are traversed. So, the output of the preorder traversal of the above tree is -

A → B → D → E → C → F → G

To know more about the preorder traversal in the data structure, you can follow the link Preorder traversal.

Postorder traversal

This technique follows the 'left-right root' policy. It means that the first left subtree of the root node is traversed, after that recursively traverses the right subtree, and finally, the root node is traversed. As the root node is traversed after (or post) the left and right subtree, it is called postorder traversal.

So, in a postorder traversal, each node is visited after both of its subtrees.

The applications of postorder traversal include -

It is used to delete the tree.
It can also be used to get the postfix expression of an expression tree.

Algorithm

Until all nodes of the tree are not visited

Step 1 - Traverse the left subtree recursively.
Step 2 - Traverse the right subtree recursively.
Step 3 - Visit the root node.

Example

Now, let's see the example of the postorder traversal technique.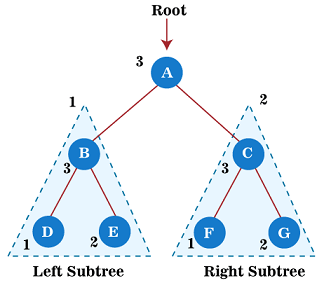

Now, start applying the postorder traversal on the above tree. First, we traverse the left subtree B that will be traversed in postorder. After that, we will traverse the right subtree C in postorder. And finally, the root node of the above tree, i.e., A, is traversed.

So, for left subtree B, first, its left subtree D is traversed. Since node D does not have any children, traverse the right subtree E. As node E also does not have any children, move to the root node B. After traversing node B, the traversal of the left subtree of root node A is completed.

Now, move towards the right subtree of root node A that is C. So, for right subtree C, first its left subtree F is traversed. Since node F does not have any children, traverse the right subtree G. As node G also does not have any children, therefore, finally, the root node of the right subtree, i.e., C, is traversed. The traversal of the right subtree of root node A is completed.

At last, traverse the root node of a given tree, i.e., A. After traversing the root node, the postorder traversal of the given tree is completed.

Therefore, all the nodes of the tree are traversed. So, the output of the postorder traversal of the above tree is -

D → E → B → F → G → C → A

To know more about the postorder traversal in the data structure, you can follow the link Postorder traversal.

Inorder traversal

This technique follows the 'left root right' policy. It means that first left subtree is visited after that root node is traversed, and finally, the right subtree is traversed. As the root node is traversed between the left and right subtree, it is named inorder traversal.

So, in the inorder traversal, each node is visited in between of its subtrees.

The applications of Inorder traversal includes -

It is used to get the BST nodes in increasing order.
It can also be used to get the prefix expression of an expression tree.

Algorithm

Until all nodes of the tree are not visited

Step 1 - Traverse the left subtree recursively.
Step 2 - Visit the root node.
Step 3 - Traverse the right subtree recursively. 

Example

Now, let's see the example of the Inorder traversal technique.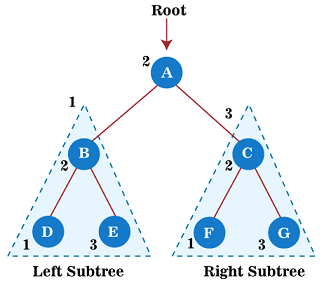

Now, start applying the inorder traversal on the above tree. First, we traverse the left subtree B that will be traversed in inorder. After that, we will traverse the root node A. And finally, the right subtree C is traversed in inorder.

So, for left subtree B, first, its left subtree D is traversed. Since node D does not have any children, so after traversing it, node B will be traversed, and at last, right subtree of node B, that is E, is traversed. Node E also does not have any children; therefore, the traversal of the left subtree of root node A is completed.

After that, traverse the root node of a given tree, i.e., A.

At last, move towards the right subtree of root node A that is C. So, for right subtree C; first, its left subtree F is traversed. Since node F does not have any children, node C will be traversed, and at last, a right subtree of node C, that is, G, is traversed. Node G also does not have any children; therefore, the traversal of the right subtree of root node A is completed.

As all the nodes of the tree are traversed, the inorder traversal of the given tree is completed. The output of the inorder traversal of the above tree is -

D → B → E → A → F → C → G

To know more about the inorder traversal in data structure, you can follow the link Inorder Traversal.

Complexity of Tree traversal techniques

The time complexity of tree traversal techniques discussed above is O(n), where 'n' is the size of binary tree.

Whereas the space complexity of tree traversal techniques discussed above is O(1) if we do not consider the stack size for function calls. Otherwise, the space complexity of these techniques is O(h), where 'h' is the tree's height.

Implementation of Tree traversal

Now, let's see the implementation of the above-discussed techniques using different programming languages.

Program: Write a program to implement tree traversal techniques in C.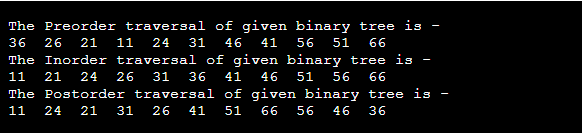

#include <stdio.h>
#include <stdlib.h>

struct node {
	int element;
	struct node* left;
	struct node* right;
};

/*To create a new node*/
struct node* createNode(int val)
{
	struct node* Node = (struct node*)malloc(sizeof(struct node));
	Node->element = val;
	Node->left = NULL;
	Node->right = NULL;

	return (Node);
}

/*function to traverse the nodes of binary tree in preorder*/
void traversePreorder(struct node* root)
{
	if (root == NULL)
		return;
	printf(" %d ", root->element);
	traversePreorder(root->left);
	traversePreorder(root->right);
}


/*function to traverse the nodes of binary tree in Inorder*/
void traverseInorder(struct node* root)
{
	if (root == NULL)
		return;
	traverseInorder(root->left);
	printf(" %d ", root->element);
	traverseInorder(root->right);
}

/*function to traverse the nodes of binary tree in postorder*/
void traversePostorder(struct node* root)
{
	if (root == NULL)
		return;
	traversePostorder(root->left);
	traversePostorder(root->right);
	printf(" %d ", root->element);
}


int main()
{
	struct node* root = createNode(36);
	root->left = createNode(26);
	root->right = createNode(46);
	root->left->left = createNode(21);
	root->left->right = createNode(31);
	root->left->left->left = createNode(11);
	root->left->left->right = createNode(24);
	root->right->left = createNode(41);
	root->right->right = createNode(56);
	root->right->right->left = createNode(51);
	root->right->right->right = createNode(66);

	printf("\n The Preorder traversal of given binary tree is -\n");
	traversePreorder(root);
	
	printf("\n The Inorder traversal of given binary tree is -\n");
	traverseInorder(root);
	
	printf("\n The Postorder traversal of given binary tree is -\n");
	traversePostorder(root);

	return 0;
}  

Output

Program: Write a program to implement tree traversal techniques in C#.

using System;

class Node {
	public int value;
	public Node left, right;

	public Node(int element)
	{
		value = element;
		left = right = null;
	}
}

class BinaryTree {
	Node root;

	BinaryTree() { root = null; }
	void traversePreorder(Node node)
	{
		if (node == null)
			return;
		Console.Write(node.value + " ");
		traversePreorder(node.left);
		traversePreorder(node.right);
	}
	
	void traverseInorder(Node node)
	{
		if (node == null)
			return;
		traverseInorder(node.left);
		Console.Write(node.value + " ");
		traverseInorder(node.right);
	}
	
	void traversePostorder(Node node)
	{
		if (node == null)
			return;
		traversePostorder(node.left);
		traversePostorder(node.right);
		Console.Write(node.value + " ");
	}
	
	
	void traversePreorder() { traversePreorder(root); }
	void traverseInorder() { traverseInorder(root); }
	void traversePostorder() { traversePostorder(root); }
	
	static void Main()
	{
		BinaryTree bt = new BinaryTree();
		bt.root = new Node(37);
		bt.root.left = new Node(27);
		bt.root.right = new Node(47);
		bt.root.left.left = new Node(22);
		bt.root.left.right = new Node(32);
		bt.root.left.left.left = new Node(12);
		bt.root.left.left.right = new Node(25);
		bt.root.right.left = new Node(42);
		bt.root.right.right = new Node(57);
		bt.root.right.right.left = new Node(52);
		bt.root.right.right.right = new Node(67);
		Console.WriteLine("The Preorder traversal of given binary tree is - ");
		bt.traversePreorder();
		Console.WriteLine();
		Console.WriteLine("The Inorder traversal of given binary tree is - ");
		bt.traverseInorder();
		Console.WriteLine();
		Console.WriteLine("The Postorder traversal of given binary tree is - ");
		bt.traversePostorder();
	}
}

Output

Program: Write a program to implement tree traversal techniques in C++.

#include <iostream>

using namespace std;

struct node {
	int element;
	struct node* left;
	struct node* right;
};

/*To create a new node*/
struct node* createNode(int val)
{
	struct node* Node = (struct node*)malloc(sizeof(struct node));
	Node->element = val;
	Node->left = NULL;
	Node->right = NULL;

	return (Node);
}

/*function to traverse the nodes of binary tree in preorder*/
void traversePreorder(struct node* root)
{
	if (root == NULL)
		return;
	cout<<" "<<root->element<<" ";
	traversePreorder(root->left);
	traversePreorder(root->right);
}

/*function to traverse the nodes of binary tree in Inorder*/
void traverseInorder(struct node* root)
{
	if (root == NULL)
		return;
	traverseInorder(root->left);
	cout<<" "<<root->element<<" ";
	traverseInorder(root->right);
}

/*function to traverse the nodes of binary tree in postorder*/
void traversePostorder(struct node* root)
{
	if (root == NULL)
		return;
	traversePostorder(root->left);
	traversePostorder(root->right);
	cout<<" "<<root->element<<" ";
}

int main()
{
	struct node* root = createNode(38);
	root->left = createNode(28);
	root->right = createNode(48);
	root->left->left = createNode(23);
	root->left->right = createNode(33);
	root->left->left->left = createNode(13);
	root->left->left->right = createNode(26);
	root->right->left = createNode(43);
	root->right->right = createNode(58);
	root->right->right->left = createNode(53);
	root->right->right->right = createNode(68);
	cout<<"\n The Preorder traversal of given binary tree is -\n";
	traversePreorder(root);
	
	cout<<"\n The Inorder traversal of given binary tree is -\n";
	traverseInorder(root);
	
	cout<<"\n The Postorder traversal of given binary tree is -\n";
	traversePostorder(root);
	return 0;
}

Output

Program: Write a program to implement tree traversal techniques in Java.

class Node {  
    public int value;  
    public Node left, right;  
  
    public Node(int element)  
    {  
        value = element;  
        left = right = null;  
    }  
}  
  
class Tree {  
    Node root;  /* root of the tree */
  
    Tree() { root = null; }  
  /*function to print the nodes of given binary in Preorder*/
    void traversePreorder(Node node)  
    {  
        if (node == null)  
            return;  
        System.out.print(node.value + " ");  
        traversePreorder(node.left);  
        traversePreorder(node.right);  
    }  
  /*function to print the nodes of given binary in Inorder*/
	void traverseInorder(Node node)  
    {  
        if (node == null)  
            return;  
        traverseInorder(node.left);  
        System.out.print(node.value + " ");  
        traverseInorder(node.right);  
    }  
	/*function to print the nodes of given binary in Postorder*/
	void traversePostorder(Node node)  
    {  
        if (node == null)  
            return;  
        traversePostorder(node.left);  
        traversePostorder(node.right);  
        System.out.print(node.value + " ");  
    }  
  

    void traversePreorder() { traversePreorder(root); }  
    void traverseInorder() { traverseInorder(root); }  
    void traversePostorder() { traversePostorder(root); }  
  
    public static void main(String args[])  
    {  
        Tree pt = new Tree();  
        pt.root = new Node(36);  
        pt.root.left = new Node(26);  
        pt.root.right = new Node(46);  
        pt.root.left.left = new Node(21);  
        pt.root.left.right = new Node(31);  
        pt.root.left.left.left = new Node(11);  
        pt.root.left.left.right = new Node(24);  
        pt.root.right.left = new Node(41);  
        pt.root.right.right = new Node(56);  
        pt.root.right.right.left = new Node(51);  
        pt.root.right.right.right = new Node(66);  
  
        System.out.println();  
		System.out.println("The Preorder traversal of given binary tree is - ");  
        pt.traversePreorder();  
        System.out.println("\n");  
		System.out.println("The Inorder traversal of given binary tree is - ");  
        pt.traverseInorder();  
        System.out.println("\n");  
		System.out.println("The Postorder traversal of given binary tree is - ");  
        pt.traversePostorder();  
        System.out.println();  
    }  
}  

Output

After the execution of the above code, the output will be -

Conclusion

In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.

So, that's all about the article. Hope it will be helpful and informative to you.

Next TopicImplementation of Queue using Stacks

← prev next →