Triangular Numbers

A triangular number is also called a Triangle number. It represents the number as an equilateral triangle spread out in a series or sequence. Others also include Cube numbers and square numbers.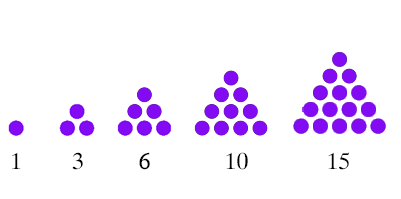

The nth Triangular Number: The number of dots in the triangular arrangement with n dots on each side equal the sum of the n natural number from 1 to n. The triangle number sequence begins from the 0^th triangle number

Examples of Triangular

• Aeroplanes flying together constitutes this formation.
• Flocks of birds fly in the triangular formation.

Examples of Triangular number includes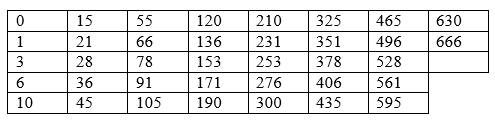

The Formula for the Triangular Number

The formula for triangular numbers is given below: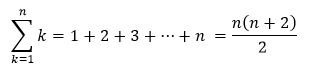

The mathematical induction can prove this formula

Now assume that for some natural number q

Proving the formula using mathematical induction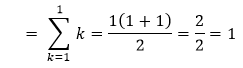

Let's assume that some natural number n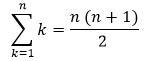

Adding (n + 1) to both sides of the equation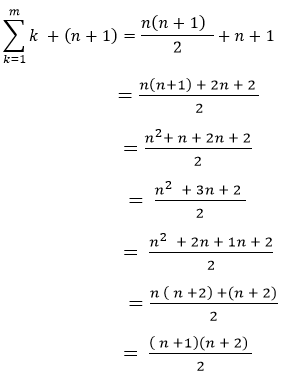

From here we can conclude that it is true for k = 1, n and for (n + 1)

Where (n + 1)/ 2 is termed a binomial coefficient. It shows the number of distinct pairs that can be chosen from n + 1 objects, and it can be expressed as

(n + 1) Factorial / (n + 1- 2) factorial 2 factorial

It has been simplified as {n (n + 1)}/2.

So, we can conclude from the above that the sum of n natural numbers gives a triangular number. We can infer that the summation of the natural number gives a triangular number.

Properties of the Triangular numbers

• The sum of two consecutive triangular numbers gives a square number.

Suppose

= 3 + 6 = 9 = 3 x 3

• If A is a triangular number, 9 * A + 1 will also be a Triangular number.

9 * A+ 1 = 9 x 6 + 1 = 55

9 * A + 1 = 9 x 10 + 1 = 91

• 2, 4, 7, or 9 cannot came at the end of triangular number.
• If A is a triangular number, then 8 * A + 1 will always be a perfect square

8 * A + 1 = 8 * 3 + 1= 24 + 1 = 25 = 5 x 5

8 * A + 1 = 8 * 6 + 1 = 48 + 1 = 49 = 7 x 7

• The Addition or sum of n consecutive cubes from 1 is equivalent to the square of the nth triangular number.

A² = 10 x 10 = 100 = 1 x 1 x 1 + 2 x 2 x 2 + 3 x 3 x 3 + 4 x 4 x 4 x 4

A² = 15 x 15 = 225 = 1 x 1 x 1 + 2 x 2 x 2 + 3 x 3 x 3 + 4 x 4 x 4 + 5 x 5 x 5.

• Four specific triangular number in AP (Arithmetic Progression) doesn't exist.
• The sum or Addition of the squares of two consecutive triangular numbers gives a triangular number.

A₁² + A² = 1 x 1 + 3 x 3 = 10

A₁² + A₂² = 3 x3 + 6 x 6 = 9 + 36 = 49

A₁² + A₂² = 6 x 6 + 10 x10 = 36 + 100 = 136

Some Interesting Facts Related to Triangular Numbers

• All perfect numbers also come in the category of a triangular number
• Sequence numbers 1, 11, 111, 1111, 11111, …… are all triangular numbers in base 9.
• 3 is the only triangular number that is prime.

Palindromic Triangular number

These numbers can be read the same forward as well as backward. For example, 55, 66, 171, 595, 666, 3003, 5995, 8778, 15051, 66066, etc., are called Palindromic Triangular Numbers. 28 Palindromic Triangular numbers are there from Types of Triangular Numbers

Reversible Triangular Number

There are some triangular numbers when their reversal also results in the triangular number. Examples of reversible triangular numbers include 190, 171,153, 120, 820, 15051, and 17578.

Square Triangular Number

An infinite triangular number exists in the series, and the series gives squares. An example includes 1, 36, 1225, 41616….

Applications of Triangular Number

A triangular number is mostly applied in the Handshake problem, and it is one of the most prominent applications.

Solved Example

Question: Determine the next triangular number in the series 45, 55, ……

Difference = 55 - 45 = 10.

To determination of the difference for the next term, we need to add one more to the difference, and it will come as

= 10 + 1 = 11

Hence the next term

55 + 11 = 66.

Question: Initial triangular numbers are 1, 3, 6, 10, 15, and 21. Produce general formula for finding the nth triangular number.

General Formula = n + (n - 1) + (n - 2) + …. + 2 + 1

For example, we want to determine the 4^th number, so we put the value as n = 4 into the equation and will get the desired result.