Unit Circle

In geometry, the unit circle is a special type of circle. It is used to explain the trigonometrical concept. We can use it to explain all possible measures of angles from 0-degree to 360-degrees. In brief, the unit circle denotes all the possible angles that exist with positive and negative values.

In this section, we will learn what is the unit circle, parts of the unit circle, and how to find the points of the unit circle.

What is the unit circle?

A circle with a unit radius is called unit circle. It means a circle whose radius is 1 unit is called the unit circle. The center coordinates of a unit circle are (0, 0).

In other words, any straight line drawn from the center to any point on the edge of the circle, the length of that line will always equal to 1.

Points of Unit circle

The points of the unit circle make mathematics easy for us. For example, in a unit circle for any angle θ, the trig-values for sine and cosine are clearly nothing more than sin (θ)=y and cos (θ)=x.

To understand the points of a unit circle, first, we learn the quadrant system in trigonometry. The following figure shows the four quadrants.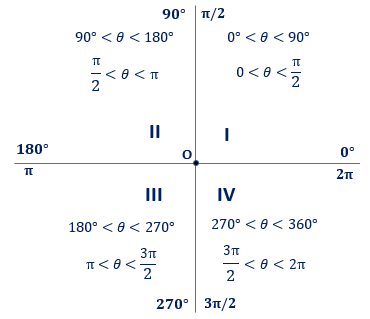

• The angles between 0° to 90° lies in the first quadrant.
• The angles between 90° to 180° lies in the second quadrant.
• The angles between 180° to 270° lies in the third quadrant.
• The angles between 270° to 360° lies in the fourth quadrant.

The following image illustrates which quadrant will have the positive or negative value of sine and cosine.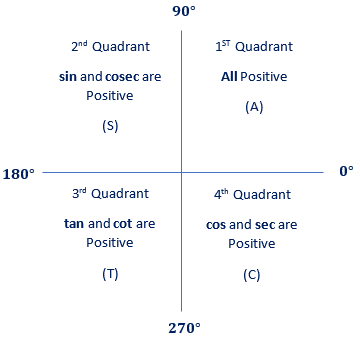

Now move to the unit circle.

First, we draw the two secants vertically and horizontally. It divides the circle into four quadrants (counter-clockwise) labeled as 1^st, 2^nd, 3^rd, 4^th quadrants, respectively. Write the coordinates of each intersection point.

We can define the trigonometry functions sine and cosine on the unit circle. Suppose, (x, y) is a point on the unit circle, and the chords from the center to the point (x, y) makes an angle of θ degree from the x-axis, as we have shown in the following figure. Then, the equation x²+y²=1 gives the following relation:

Substituting the values of x and y by cosine and sine, respectively, we get:

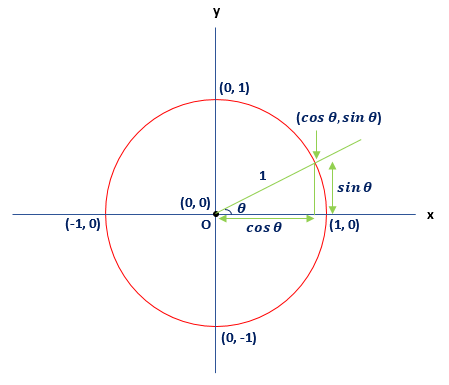
We can observe from the unit circle that the values of sine and cosine will never be more than 1 or less than -1. Hence, the values of sine and cosine lie between 1 and -1.

When we reach one-fourth and three-fourths of the circle (means 90°,180°,270°), we do not define the tangent for these angles. Now, we further divide each quadrant into four subparts. These parts make the angles of 0°,30°,45°,60°,and 90°.

Note: We will not consider 0°,90°,180°and 270°, in any quadrant. It is for understanding purposes, only. To write the values of other angles of all quadrant, we must memorize the trig-function values.

When we have done all the above steps, the first quadrant looks like the following figure: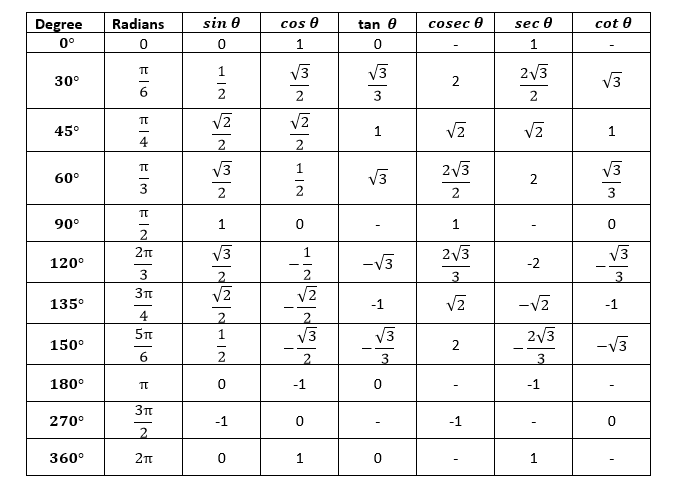

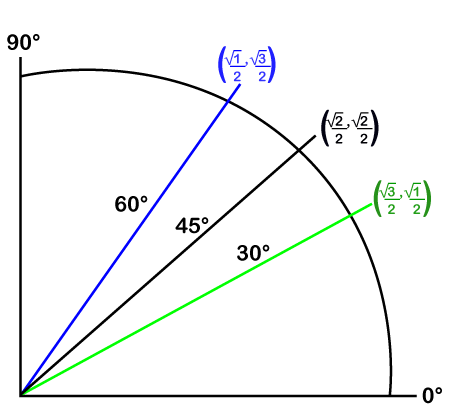
The following unit circle showing the coordinate of certain points.