Unit Vector Definition

A unit vector is a vector that has a magnitude of 1 and is used in mathematics and physics to simplify calculations and describe physical quantities. In this explanation, we will cover the definition of a unit vector, how to calculate a unit vector and some applications of unit vectors.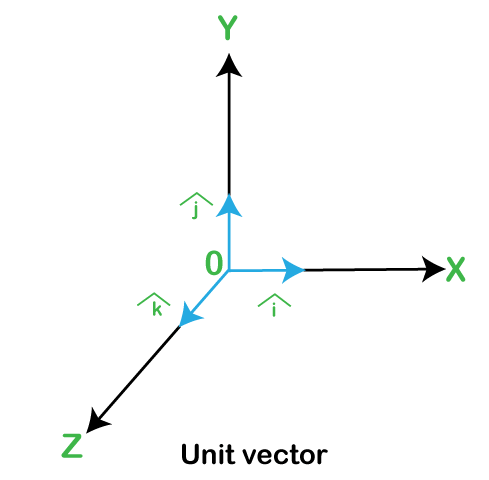

Definition of a Unit Vector

A unit vector is a vector that has a magnitude of 1. In other words, it is a vector that is normalized to have a length of 1. A vector is a mathematical object that has both magnitude and direction. The magnitude of a vector represents its length or size, while the direction of the vector represents the direction in which it is pointing. A unit vector is important because it allows us to describe a direction without worrying about the magnitude of the vector.

How to Calculate a Unit Vector

To calculate a unit vector, we first need to find the magnitude of the vector we want to normalize. The magnitude of a vector is found using the Pythagorean theorem, which states that the magnitude of a vector is equal to the square root of the sum of the squares of its components. For example, if we have a vector v = (3, 4), the magnitude of the vector is found using the following equation:

|v| = sqrt(3^2 + 4^2) = 5

Once we have found the magnitude of the vector, we can normalize it by dividing each component of the vector by the magnitude. The resulting vector will have a magnitude of 1 and will be a unit vector. Continuing with our previous example, the unit vector u that corresponds to v can be found using the following equation:

u = v/|v| = (3/5, 4/5)

Applications of Unit Vectors

• Unit vectors have many applications in mathematics and physics. One of the most important applications is in vector calculus. In this branch of mathematics, unit vectors are used to define the gradient, divergence, and curl of a vector field. The gradient of a vector field represents the rate of change of the field in a given direction, while the divergence and curl of a vector field represent the flow and rotation of the field, respectively.
• By using unit vectors, we can simplify the calculations involved in these operations and make them easier to understand.
• Another important application of unit vectors is in physics. In mechanics, unit vectors are used to represent forces and velocities. For example, the unit vector that represents the direction of a force is used to calculate the work done by the force on an object. Similarly, the unit vector that represents the direction of a velocity is used to calculate the momentum of an object. By using unit vectors, we can simplify the equations involved in these calculations and make them easier to solve.

Directional Significance of Unit Vectors

Unit vectors are used to define directions in three-dimensional space. In three-dimensional space, we have three axes - x, y, and z - and each axis is associated with a unit vector. The unit vector in the positive x-direction is denoted by i, the unit vector in the positive y-direction is denoted by j, and the unit vector in the positive z-direction is denoted by k. These three unit vectors form an orthonormal basis for three-dimensional space. Any vector in three-dimensional space can be expressed as a linear combination of these three unit vectors.

For example, consider a vector v = (2, 3, 4). To express this vector in terms of the i, j, and k unit vectors, we can write:

v = 2i + 3j + 4k

This notation tells us that the vector v has a component of 2 in the x-direction, 3 in the y-direction, and 4 in the z-direction.

Unit Vectors in Two-Dimensional Space

While the above discussion focused on unit vectors in three-dimensional space, unit vectors can also be defined in two-dimensional space. In two-dimensional space, there are only two axes - the x-axis and the y-axis - and each axis is associated with a unit vector. The unit vector in the positive x-direction is denoted by i, and the unit vector in the positive y-direction is denoted by j. Any vector in two-dimensional space can be expressed as a linear combination of these two unit vectors.

For example, consider a vector v = (3, 4). To express this vector in terms of the i and j unit vectors, we can write:

v = 3i + 4j

This notation tells us that the vector v has a component of 3 in the x-direction and 4 in the y-direction.

Unit Vectors in Polar Coordinates

In addition to Cartesian coordinates, unit vectors can also be expressed in polar coordinates. In polar coordinates, a point is described by its distance from the origin (called the radius or magnitude) and the angle that the line connecting the point to the origin makes with the positive x-axis (called the angle or argument). In two-dimensional polar coordinates, a unit vector can be defined as:

u = cos(x)i + sin(x)j

where x is the angle that the unit vector makes with the positive x-axis. This definition ensures that the unit vector has a magnitude of 1.

In three-dimensional polar coordinates, unit vectors can be defined using spherical coordinates or cylindrical coordinates, depending on the application. These coordinate systems involve specifying the distance from the origin, the angle that the line connecting the point to the origin makes with a reference direction, and the angle that the line connecting the point to the origin makes with the positive z-axis (in the case of spherical coordinates) or the height of the point above the xy-plane (in the case of cylindrical coordinates).

Conclusion

In summary, a unit vector is a vector that has a magnitude of 1. It is used in mathematics and physics to simplify calculations and describe physical quantities. To calculate a unit vector, we need to find the magnitude of the vector and divide each component of the vector by the magnitude. Unit vectors have many applications in vector calculus and physics, and they allow us to simplify calculations and make them easier to understand.

Unit vectors are an important mathematical concept with many applications in various fields, including physics, engineering, and computer graphics. They allow us to describe directions without worrying about magnitudes and simplify calculations involving vector operations. Unit vectors can be defined in Cartesian coordinates, polar coordinates, and other coordinate systems, and they have directional significance in three-dimensional space. By understanding unit vectors, we can better understand the behavior of vectors and their applications in real-world problems.