Gate Level Modeling

In Verilog, most of the digital designs are done at a higher level of abstraction like RTL. However, it becomes natural to build smaller deterministic circuits at a lower level by using combinational elements such as AND and OR.

Modeling done at this level is called gate-level modeling as it involves gates and has a one to one relationship between a hardware schematic and the Verilog code.

Verilog supports a few basic logic gates known as primitives, as they can be instantiated, such as modules, and they are already predefined.

Gate level modeling is virtually the lowest level of abstraction because the switch-level abstraction is rarely used. Gate level modeling is used to implement the lowest-level modules in a design, such as multiplexers, full-adder, etc. Verilog has gate primitives for all basic gates.

Verilog supports built-in primitive gates modeling. The gates supported are multiple-input, multiple-output, tri-state, and pull gates.

The multiple-input gates are and, nand, or, nor, xor, and xnor whose number of inputs are two or more, and has only one output.

The multiple-output gates are buf and not whose output is one or more and has only one input.

The language also supports the modeling of tri-state gates, including bufif0, bufif1, notif0, and notif1. These gates have one input, one control signal, and one output.

The pull gates are pullup and pulldown with a single output only.

Syntax

Following is the basic syntax for each type of gates with zero delays, such as:

and | nand | or | nor | xor | xnor [instance name] (out, in1, ..., inN);      // [] is optional and | is selection 
buf | not [instance name] (out1, out2, ..., out2, input); 
bufif0 | bufif1 | notif0 | notif1 [instance name] (outputA, inputB, controlC); 
pullup | pulldown [instance name] (output A); 

One can also have multiple instances of the same type of gate in one construct separated by a comma:

and [inst1] (out11, in11, in12), [inst2] (out21, in21, in22, in23), [inst3] (out31, in31, in32, in33); 

The gate-level modeling is useful when a circuit is a simple combinational, such as a multiplexer. A multiplexer is a simple circuit that connects one of many inputs to an output.

Gate Primitives

Gate primitives are predefined modules in Verilog, which are ready to use. There are two classes of gate primitives:

Single input gate primitives
Multiple input gate primitives

1. Single input gate primitives

Single input gate primitives have a single input and one or more outputs. The gate primitive are not, buf, notif, and bufif also have a control signal.

The gates propagate only if the control signal is asserted, else the output is high impedance state.

1.1 Not, buf Gates

These gates have only one scalar input but may have multiple outputs.

buf stands for a buffer and transfer the value from input to the output without any change in polarity.

not stands for an inverter which inverts the polarity of the signal at its input. So a 0 at its input will yield a 1 and vice versa.

Syntax

module gates (	input a, b,
				output c, d);

	buf (c, a, b); 	// c is the output, a and b are inputs
  	not (d, a, b);	// d is the output, a and b are inputs

endmodule

Example

module tb;
   reg a, b;
   wire c, d;
   integer i;
gates u0 ( .a(a), .b(b), .c(c), .d(d));
   initial begin
	{a, b} = 0;
   $monitor ("[T=%0t a=%0b b=%0b c(buf)=%0b d(not)=%0b", $time, a, b, c, d);
	for (i = 0; i < 10; i = i+1) begin
		#1 	a <= $random;
			b <= $random;
	end
end
endmodule

1.2 Bufif, Notif Gates

Bufif and notif primitives are buffers and inverters, respectively, with an additional control signal to enable the output is available through bufif and notif primitives.

These gates have a valid output only if the control signal is enabled else, and the output will be in high impedance.

There are two versions of these, one with the normal polarity of control indicated by a 1 such as bufif1 and notif1. And second with the inverted polarity of control indicated by a 0 such as bufif0 and notif0.

Syntax

module bufif_notif_gates (output c, d, input a, b);
bufif (c, a, b);   // c is the output, a and b are inputs
notif (d, a, b);  // d is the output, a and b are inputs
endmodule

Example

module bufif_notif_gates_tb;
  reg a, b;
  wire c, d;
  bufif_notif_gates Instance0 (c, d, a, b);
  initial begin
    a = 0; b = 0;
 #1 a = 0; b = 1; 
 #1 a = 1; b = 0;
 #1 a = 1; b = 1;
  end
  initial begin
    $monitor ("T=%t| a=%b |b=%b| c(bufif)=%b |d(notif)=%b", $time, a, b, c, d);
  end
endmodule

2. Multiple Input Gate Primitives

Multiple input gate primitives include AND, OR, XOR, NAND, NOR, and XNOR. They may have multiple inputs and a single output.

2.1 AND, OR, XOR Gates

An AND, OR, and an XOR gate need multiple scalar inputs and produce a single scalar output.

The first terminal in the argument list to these primitives is the output, which changed as any inputs shift.

Syntax

module and_or_xor_gates (output c, d, e, input a, b);
  and (c, a, b);   // c is the output, a and b are inputs
  or  (d, a, b);  // d is the output, a and b are inputs
  xor (e, a, b);   // e is the output, a and b are inputs
endmodule

Example

module and_or_xor_gates_tb;
reg a, b;
wire c, d, e;
and_or_xor_gates Instance0 (c, d, e, a, b);
 initial begin
   a = 0; b = 0;
   #1 a = 0; b = 1; 
   #1 a = 1; b = 0;
   #1 a = 1; b = 1;
 end
 initial begin
   $monitor ("T=%t |a=%b |b=%b |c(and)=%b |d(or)=%b |e(xor)=%b", $time, a, b, c, d, e);
 end
endmodule

1.2 NAND, NOR, XNOR Gates

The inverse of all the above gates is NAND, NOR, and XNOR. The same design from above is reused only that the primitives are interchanged with their inverse versions.

Syntax

module nand_nor_xnor_gates (output c, d, e, input a, b);
 nand (c, a, b); // c is the output, a and b are inputs 
 nor (d, a, b); // d is the output, a and b are inputs 
 xnor (e, a, b); // e is the output, a and b are inputs
endmodule 

Example

module nand_nor_xnor_gates_tb;
reg a, b;
wire c, d, e;
nand_nor_xnor_gates Instance0 (c, d, e, a, b);
  initial begin
    a = 0; b = 0;
 #1 a = 0; b = 1; 
 #1 a = 1; b = 0;
 #1 a = 1; b = 1;
end
  initial begin
    $monitor ("T=%t |a=%b |b=%b |c(nand)=%b |d(nor)=%b |e(xnor)=%b", $time, a, b, c, d, e);
  end
endmodule

All these gates may also have more than two inputs.

module all_gates (output x1, y1, z1, x2, y2, z2 , input a, b, c, d);
  and (x1, a, b, c, d);   // x1 is the output, a, b, c, d are inputs
  or  (y1, a, b, c, d);  // y1 is the output, a, b, c, d are inputs
  xor (z1, a, b, c, d);   // z1 is the output, a, b, c, d are inputs
  nand (x2, a, b, c, d); // x2 is the output, a, b, c, d are inputs
  nor (y2, a, b, c, d); // y2 is the output, a, b, c, d are inputs 
  xnor (z2, a, b, c, d); // z2 is the output, a, b, c, d are inputs
endmodule

Gate Level Modeling of a Multiplexer

The gate-level circuit diagram of 4x1 mux is shown below. It is used to write a module for 4x1 mux.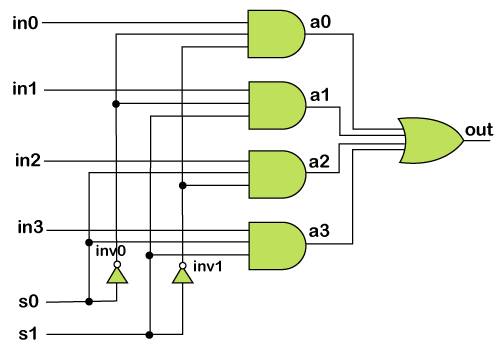

module 4x1_mux (out, in0, in1, in2, in3, s0, s1);

// port declarations
output out; // Output port.
input in0, in1, in2. in3; // Input ports.
input s0, s1; // Input ports: select lines.

// intermediate wires
wire inv0, inv1; // Inverter outputs.
wire a0, a1, a2, a3; // AND gates outputs.

// Inverters.
not not_0 (inv0, s0);
not not_1 (inv1, s1);

// 3-input AND gates.
and and_0 (a0, in0, inv0, inv1);
and and_1 (a1, in1, inv0, s1);
and and_2 (a2, in2, s0, inv1);
and and_3 (a3, in3, s0, s1);

// 4-input OR gate.
or or_0 (out, a0, a1, a2, a3);

endmodule

Gate Level Modeling of Full-adder

Here is the implementation of a full adder using the half adder.

1. Half adder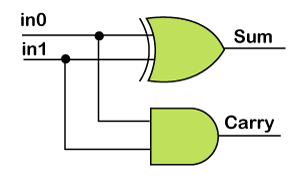

module half_adder (sum, carry, in0, in1);

output sum, carry;
input in0, in1;

// 2-input XOR gate.
xor xor_1 (sum, in0, in1);

// 2-input AND gate.
and and_1 (carry, in0, in1);

endmodule

2. Full adder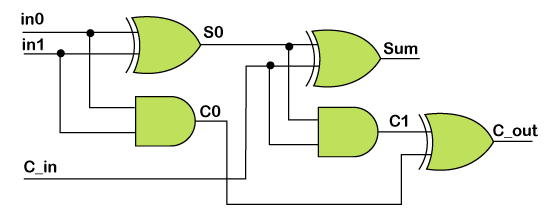

module full_adder (sum, c_out, ino, in1, c_in);

output sum, c_out;
input in0, in1, c_in;

wire s0, c0, c1;
// Half adder: port connecting by order.
half_adder ha_0 (s0, c0, in0, in1);

// Half adder : port connecting by name.
half_adder ha_1 (.sum(sum),
                .in0(s0),
                .in1(c_in),
                .carry(c1));

// 2-input XOR gate, to get c_out.
xor xor_1 (c_out, c0, c1);

endmodule

Next TopicSwitch Level Modeling

← prev next →