Verilog Gray Counter

Gray code is a kind of binary number system where only one bit will change at a time. Today gray code is widely used in the digital world. It will be helpful for error correction and signal transmission. The Gray counter is also useful in design and verification in the VLSI domain.

A Gray Code encodes integers as sequences of bits with the property that the representations of adjacent integers differ in exactly one binary position.

There are different types of gray codes, such as Balanced, Binary reflected, Maximum Gap, and Antipodal Gray code.

Counters have a primary function of producing a specified output sequence and are sometimes referred to as pattern generators.

Design

In a gray code, only one bit changes at one time. This design code has two inputs, clock and reset signals and one 4 bit output that will generate gray code.

First, if the rstn signal is high, then the output will be zero, and as soon as rstn goes low, on the rising edge of clk, the design will generate a four-bit gray code and continue to generate at every rising edge of clk signal.

This design code can be upgraded and put binary numbers as input, and this design will work as a binary to gray code converter.

module gray_ctr
  # (parameter N = 4)

  (	input 	clk,
	input 	rstn,
	output reg [N-1:0] out);

	reg [N-1:0] q;

	always @ (posedge clk) begin
		if (!rstn) begin
    	q <= 0;
    		out <= 0;
      end else begin
  		q <= q + 1;
`ifdef FOR_LOOP
    	for (int i = 0; i < N-1; i= i+1) begin
      	out[i] <= q[i+1] ^ q[i];
    	end
    	out[N-1] <= q[N-1];
`else
			out <= {q[N-1], q[N-1:1] ^ q[N-2:0]};
`endif
    end
	end
endmodule

Hardware Schematic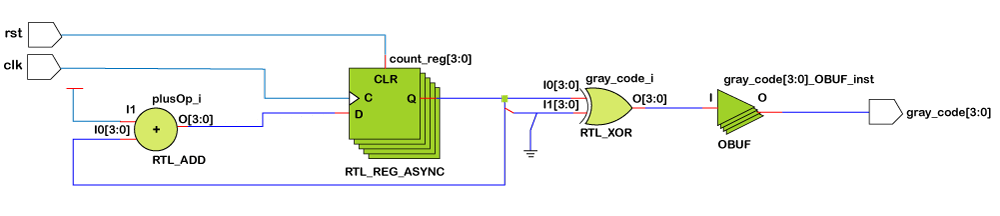

Testbench

module tb;
  parameter N = 4;

  reg clk;
  reg rstn;
  wire [N-1:0] out;

  gray_ctr u0 (	.clk(clk),
               .rstn(rstn),
               .out(out));

  always #10 clk = ~clk;

  initial begin
    {clk, rstn} <= 0;

    $monitor ("T=%0t rstn=%0b out=0x%0h", $time, rstn, out);

    repeat(2) @ (posedge clk);
    rstn <= 1;
    repeat(20) @ (posedge clk);
    $finish;
  end
endmodule

And it produces the following output, such as:

ncsim> run
T=0 rstn=0 out=0xx
T=10 rstn=0 out=0x0
T=30 rstn=1 out=0x0
T=50 rstn=1 out=0x1
T=70 rstn=1 out=0x3
T=90 rstn=1 out=0x2
T=110 rstn=1 out=0x6
T=130 rstn=1 out=0x7
T=150 rstn=1 out=0x5
T=170 rstn=1 out=0x4
T=190 rstn=1 out=0xc
T=210 rstn=1 out=0xd
T=230 rstn=1 out=0xf
T=250 rstn=1 out=0xe
T=270 rstn=1 out=0xa
T=290 rstn=1 out=0xb
T=310 rstn=1 out=0x9
T=330 rstn=1 out=0x8
T=350 rstn=1 out=0x0
T=370 rstn=1 out=0x1
T=390 rstn=1 out=0x3
T=410 rstn=1 out=0x2
Simulation complete via $finish(1) at time 430 NS + 0

Balanced Gray Code

In balanced Gray codes, the number of changes in different coordinate positions is as close as possible.

A Gray code is uniform or uniformly balanced if its transition counts are all equal.

Gray codes can also be exponentially balanced if all of their transition counts are adjacent powers of two, and such codes exist for every power of two.

For example, a balanced 4-bit Gray code has 16 transitions, which can be evenly distributed among all four positions (four transitions per position), making it uniformly balanced.

1 1 1 1 1 1 0 0 0 0 0 0 1 1 0 
0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 
0 0 0 1 1 1 1 1 0 0 1 1 1 0 0 
0 0 1 1 0 0 0 0 0 1 1 1 1 1 1

n-ary Gray Code

There are many specialized types of Gray codes other than the binary-reflected Gray code. One such type of Gray code is the n-ary Gray code, also known as a non-Boolean Gray code. As the name implies, this type of Gray code uses non-Boolean values in its encodings.

For example, a 3-ary ternary Gray code would use the values {0, 1, and 2}. The (n, k)-Gray code is the n-ary Gray code with k digits. The sequence of elements in the (3, 2)-Gray code is: {00, 01, 02, 12, 11, 10, 20, 21, and 22}.

The (n, k)-Gray code may be constructed recursively, as the BRGC, or may be constructed iteratively.

Monotonic Gray Codes

Monotonic codes are useful in interconnection networks theory, especially for minimizing dilation for linear arrays of processors.

If we define the weight of a binary string to be the number of 1s in the string, then although we clearly cannot have a Gray code with strictly increasing weight, we may want to approximate this by having the code run through two adjacent weights before reaching the next one.

Beckett-Gray Code

Another type of Gray code, the Beckett-Gray code, is named for Irish playwright Samuel Beckett, who was interested in symmetry. His play Quad features four actors and is divided into sixteen time periods. Each period ends with one of the four actors entering or leaving the stage.

The play begins with an empty stage, and Beckett wanted each subset of actors to appear on stage exactly once. A 4-bit binary Gray code can represent the set of actors currently on stage.

However,

Beckett placed an additional restriction on the script: he wished the actors to enter and exit so that the actor who had been on stage the longest would always be the one to exit.

The actors could then be represented by a first-in, first-out (FIFO) queue so that the actor being dequeued is always the one who was enqueued first.

Beckett was unable to find a Beckett-Gray code for his play, and indeed, an exhaustive listing of all possible sequences reveals that no such code exists for n = 4. It is known today that such codes do exist for n = 2, 5, 6, 7, and 8, and do not exist for n = 3 or 4.

Snake-in-the-box Codes

Snake-in-the-box codes, or snakes, are the sequences of nodes of induced paths in an n-dimensional hypercube graph, and coil-in-the-box codes, or coils, are the sequences of nodes of induced cycles in a hypercube.

Viewed as Gray codes, these sequences have the property of detecting any single-bit coding error.

Single-track Gray Code

Another kind of Gray code is the single-track Gray code (STGC) developed by Norman B. Spedding and refined by Hiltgen, Paterson and Brandestini in "Single-track Gray codes" (1996).

The STGC is a cyclical list of P unique binary encodings of length n such that two consecutive words differ in exactly one position. When the list is examined as a P × n matrix, each column is a cyclic shift of the first column.

The name comes from their use with rotary encoders, where many tracks are being sensed by contacts, resulting in each in an output of 0 or 1. To reduce noise due to different contacts not switching the same moment in time, one preferably sets up the tracks so that the contacts' data output is in Gray code.

To get high angular accuracy, one needs lots of contacts; to achieve at least 1-degree accuracy, one needs at least 360 distinct positions per revolution, which requires a minimum of 9 bits of data and the same number of contacts.

If all contacts are placed at the same angular position, then 9 tracks are needed to get a standard BRGC with at least 1-degree accuracy. However, if the manufacturer moves a contact to a different angular position but at the same distance from the center shaft, then the corresponding "ring pattern" needs to be rotated the same angle to give the same output.

Two-dimensions Gray Code

Two-dimensional Gray codes are used in communication to minimize the number of bit errors in quadrature amplitude modulation adjacent points in the constellation.

In a standard encoding, the horizontal and vertical adjacent constellation points differ by a single bit, and adjacent diagonal points differ by 2 bits.

Next TopicFile Operations

← prev next →