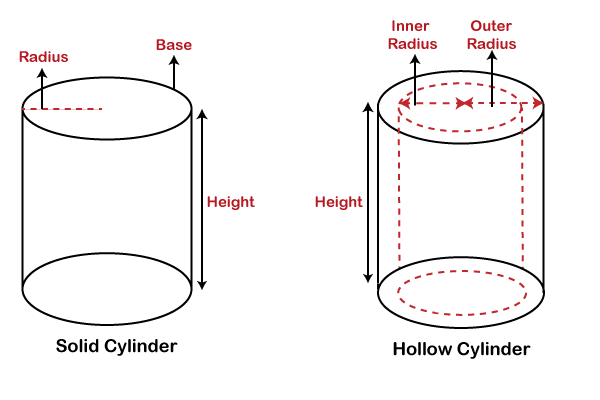
Volume of a Cylinder

In this section, we will learn the formula of the volume of a cylinder and how to find the volume of a cylinder along with proper examples.

A cylinder is a 3D geometrical shape with the two-circular base. It has two circular bases, one at top and the other at the bottom. We can also define a cylinder as an arrangement of circular disks in stacked form. There are two types of cylinders:

• Cylinder or Solid Cylinder
• Hollow Cylinder

Definition

The number of cubic units that will exactly fill a cylinder is called the volume of the cylinder. In other words, the space covered by a cylinder is called the volume of a cylinder.

The Volume of Cylinder Formula

It is the product of the area of base and height of the cylinder.

Volume of a Hollow Cylinder

A cylinder that is hollow from inside is called a hollow cylinder. There are two radii in the hollow cylinder. One for the inner cylinder and the other for an outer cylinder formed by the base.

Suppose, r₁ is the radius of the outer circle, r₂ is the radius of the inner circle, and h is the height of the cylinder, then the volume of the hollow cylinder will be:

How to Find Volume of a Cylinder

We can find the volume of a cylinder by multiplying the area of a circle by the height of the cylinder.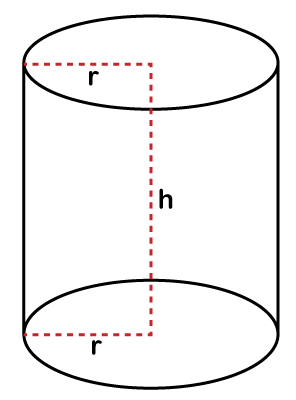

We know the formula of the area of a circle:

The Area of a Circle (A)= πr²

Multiply the area of a circle by the height of the cylinder, we get the volume of the cylinder. Since,

Where:

π: It is a constant whose value is 3.142 or 22/7.

r: It is the radius of the cylinder.

h: It is the height of the cylinder.

Note: The radius and height must be in the same unit. Convert the units if they are different.

Unit of Volume

The unit of the volume is a cubic unit or unit³. For example, if the radius and height are given in centimeters, the volume will also in centimeters, and the unit will be cubic centimeters or cm³.

Let's see some examples.

Example 1: The radius of a cylinder is 5 cm, and the height is 12 cm. Calculate the volume of the cylinder. Take π=.

Solution:

Given, radius (r) = 5 cm

Height (h) = 12 cm

π=

Volume (V) =?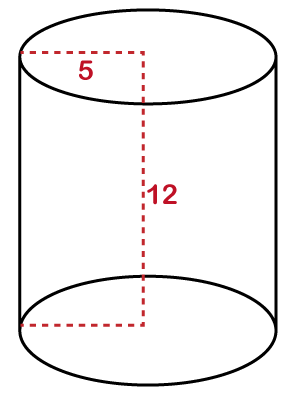

We know the formula of volume of a cylinder:

V= πr² h

Putting the values in the above formula, we get: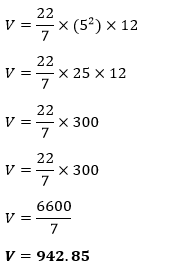

Hence, the volume of the cylinder is 942.85 cm³.

Example 2: Calculate the volume of a cylinder whose radius is 3 cm and the height is 6 cm. (π=3.14)

Solution:

Given, radius (r) = 3 cm

Height (h) = 6 cm

π=3.14

Volume (V) =?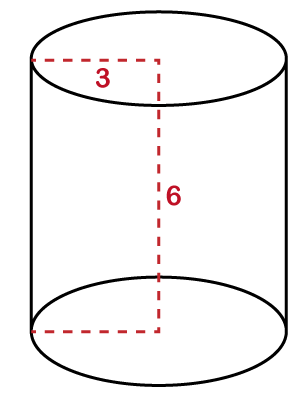

We know the formula of volume of a cylinder:

V= πr² h

Putting the values in the above formula, we get:

V=3.14×(3²)×6
V=3.14×9×6
V=3.14×54
V=169.56

Hence, the volume of the cylinder is 169.56 cm3.

Example 3: What is the volume of the cylinder given below.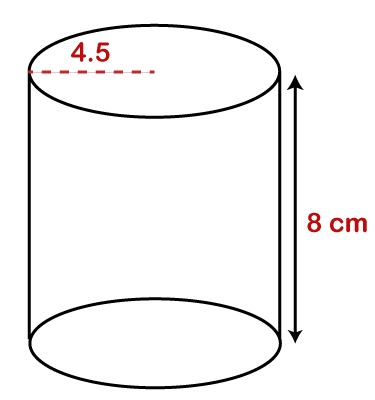

Solution:

Given, radius (r) = 4.5 cm

Height (h) = 8 cm

Volume (V) =?

We know the formula of volume of a cylinder:

V= πr² h

Putting the values in the above formula, we get:

V=3.14×(4.5²)×8
V=3.14×20.25×8
V=508.68

Hence, the volume of the cylinder is 508.68 cm³.

Example 4: The volume of a cylinder is 255 cm³ and the height is 15 cm. Find the radius (r) of the cylinder.

Solution:

Given, Volume (V) = 255 cm³

Height (h) = 15 cm

π=3.14

Radius (r) =?

We know the formula of volume of a cylinder:

V= πr² h

Putting the values in the above formula, we get: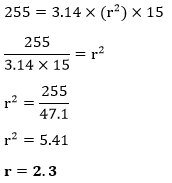

Hence, the radius of the cylinder is 2.3 cm.

Example 5: Find the volume of the hollow cylinder.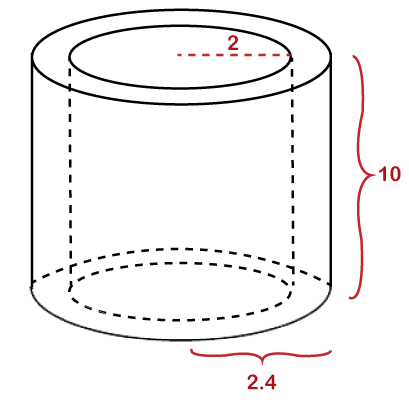

Solution:

Given, radius of outer cylinder (r₁) = 2.4 cm

radius of inner cylinder (r₂) = 2 cm

Height (h) = 10 cm

π=3.14

Volume (V) =?

We know the formula of volume of the hollow cylinder: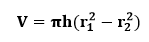

Putting the values in the above formula, we get:

V=3.14×10×(2.4^{2-22)
V=3.14×10×(5.76-4)
V=3.14×10×(1.76)
V=55.264}

Hence, the volume of the hollow cylinder is 55.264 cm³.

Example 6: The outer and inner radius of a pipe is 8 and 6 cm, respectively. The height of the pipe is 15 cm. Find the volume of the pipe. Take pi=3.14.

Solution:

Given, radius of outer cylinder (r₁) = 8 cm

radius of inner cylinder (r₂) = 6 cm

Height (h) = 15 cm

π=3.14

Volume (V) =?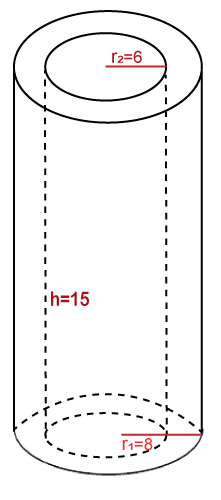

We know the formula of volume of the hollow cylinder: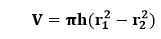

Putting the values in the above formula, we get:

V=3.14×15×(8²-6²)
V=3.14×15×(64-36)
V=3.14×15×2
V=1318.8

Hence, the volume of the hollow cylinder is 1318.8 cm³.