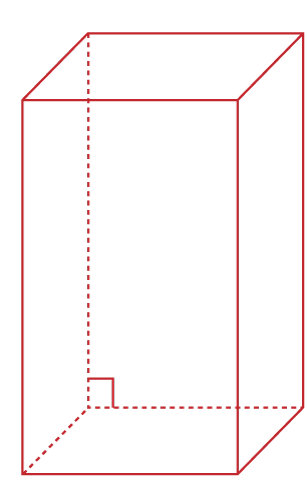
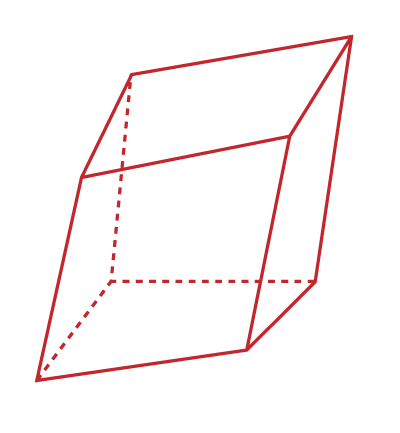
Volume of a Rectangular Prism

In geometry, a rectangular prism is a polyhedron (the shape whose all sides are flat) with two congruent and parallel bases. It is called prism because it forms a cross-section along the length. In this section, we will discuss the definition of a rectangular prism, types, volume formula, and the volume of a rectangular prism.

Definition

A rectangular prism is a three-dimensional solid shape that has six rectangular faces. Another name of the rectangular prism is cuboid. It has twelve edges, six faces, and eight vertices. Brick, box and book are the best examples of the rectangular prism. The following figure illustrates the shape of a rectangular prism.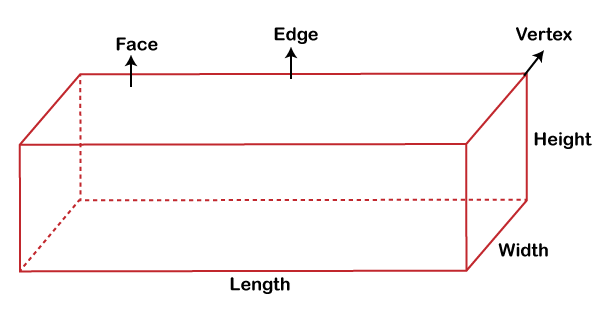

• Edge: A-line segment connected with two vertices is called an edge. There are a total of twelve edges in a rectangular prism. These edges are of different lengths.
• Face: Faces are the rectangular sides of a rectangular prism. There are a total of six faces (top, bottom, right, left, front, and back) in a rectangular prism. The opposite faces are congruent.
• Vertex: A point where three edges meet or the corners of the shape is called the vertex. There are a total of eight vertices in a rectangular prism.

Types of Rectangular Prism

There are two types of a rectangular prism:

• Right Rectangular Prism: A rectangular prism is a prism in which all the angles are right angles. In other words, a rectangular prism in which bases are perpendicular to each other is called the right rectangular prism. The following figure illustrates the shape of a right rectangular prism.
  
• Oblique Rectangular Prism: An oblique rectangular prism is a prism in which all the angles are not right angles. In other words, a rectangular prism in which bases are not perpendicular to each other is called the oblique rectangular prism. The following figure illustrates the shape of an oblique rectangular prism.
  

Properties of Rectangular Prism

• It forms a rectangular cross-section.
• It has six rectangular faces, twelve edges, and eight
• All the opposite faces are in rectangle shape.
• It is also a cuboid.

Volume of Rectangular Prism

The space occupied by a three-dimensional object is called the volume of that object.

The volume of a rectangular prism is the amount of space covered by a rectangular prism. In other words, the number of units used to fill a rectangular prism is called the volume of a rectangular prism. The unit of volume is the cubic unit or unit³.

Volume of Rectangular Prism Formula

The volume of a rectangular prism is the product of length (l), width (w), and height (h). It is denoted by V.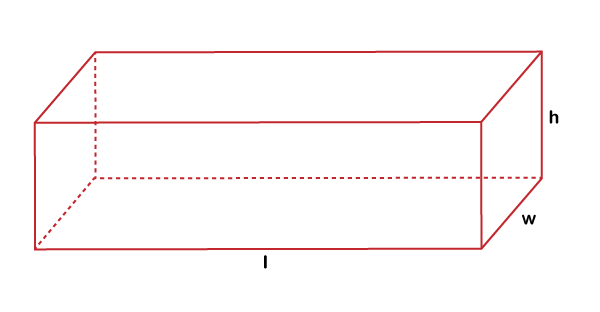

Therefore, the volume of a rectangular prism can be written as:

Or

Let's see some examples based on the above formula.

Example 1: Calculate the volume of the following rectangular box.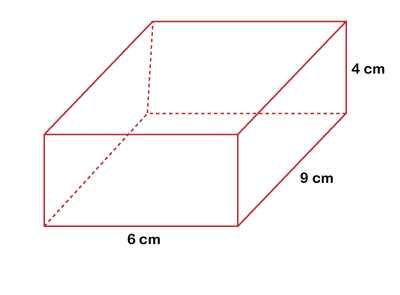

Solution:

Given, length (l) = 6 cm

          width (w) = 9 cm

          height (h) = 4 cm

According to the formula:

Putting the values of l, w, and h in the above formula, we get:

V=6×9×4
V=216

Hence, the volume of the given rectangular prism is 216 cm³.

Example 2: If the length, width, and height of a rectangular prism is 2 m, 4 m, and 9 m, respectively. Find the volume of the rectangular prism and also draw the figure.

Solution:

Given, length (l) = 2 m

          width (w) = 4 m

          height (h) = 9 m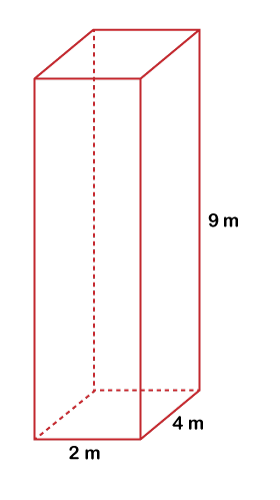

According to the formula:

Putting the values of l, w, and h in the above formula, we get:

V=2×4×9
V=72

Hence, the volume of the rectangular prism is 72 m³.

Example 3: Find the volume of the two prisms, separately, and also find the volume of the entire figure.

Solution:

Look at the above figure, we see that it is a combination of two rectangular prisms. So, first, we will separate the figure into two rectangular prisms. After that, we will find the volume of both prisms, and at last, add both volumes to find the volume of the entire figure.

Let's separate the prisms, we get the following two figures.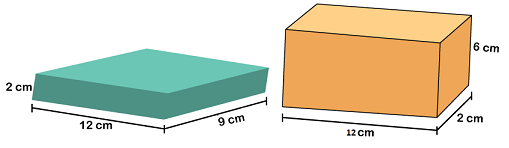

Now, we will calculate the volume of both prisms, separately.

First, we will calculate the volume of the green color figure.

According to the formula:

Putting the values in the above formula, we get:

V=12×9×2
V=216 cm³

Now we will calculate the volume of the orange color figure.

V=12×2×6
V=144 cm³

Add both the volumes to find the volume of the entire figure.

V=216+144
V=360 cm³

Hence, the volume of the entire figure is 360 cm³.

Example 4: Find the volume of the prism given below.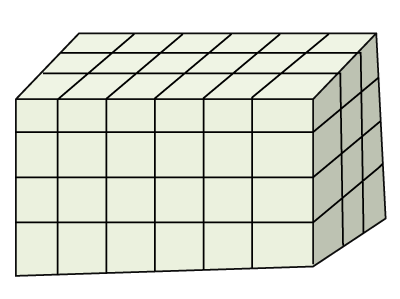

Solution:

In the given figure:

The length of the prism is: 6 units

The width of the prism is: 3 units

The height of the prism is: 4 units

According to the formula:

Putting the values in the above formula, we get:

V=6×3×4
v=72

Hence, the volume of the rectangular prism is 73 units³.