What is a Composite Number?

A composite number is a positive integer that has at least one positive integer other than 1 as a divisor. In other words, it is a positive integer that is not a prime number. For example, the first few composite numbers are 4, 6, 8, 9, 10, 12, 14, 15, and 16. These numbers can all be divided by at least one positive integer other than 1 and themselves, which means they are not prime.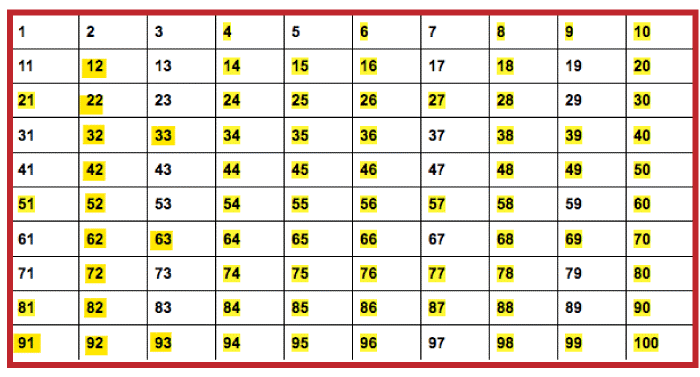

The concept of composite numbers is closely related to the concept of prime numbers. A prime number is a positive integer that has only two positive integer divisors: 1 and itself. For example, the first few prime numbers are 2, 3, 5, 7, 11, and 13. These numbers cannot be divided by any positive integer other than 1 and themselves, which means they are prime.

Ways to determine Composite Number

1. One way to determine whether a positive integer is composite is to use the process of trial division. This involves dividing the integer in question by each of the prime numbers that are less than or equal to its square root. If the integer can be divided by any of these prime numbers, then it is composite. Otherwise, it may be a prime number.

For example, consider the number 15. The prime numbers less than or equal to the square root of 15 are 2, 3, and 5. When we divide 15 by each of these numbers, we find that it is divisible by 3, which means it is a composite number.

2. Another way to determine whether a positive integer is composite is to use the Sieve of Eratosthenes, a method for finding all of the prime numbers up to a given integer. This method involves creating a list of integers from 2 to the given integer and then crossing out all of the composite numbers.

To use the Sieve of Eratosthenes, we start by crossing out all multiples of 2 from the list (since they are all composite). Then, we move on to the next number that has not been crossed out (in this case, 3) and cross out all of its multiples. We continue this process until we have crossed out all of the composite numbers in the list. The numbers that remain uncrossed are the prime numbers.

Properti

There are several properties of composite numbers that are worth noting.

1. One is that all composite numbers have at least two positive integer divisors. This is in contrast to prime numbers, which have only two positive integer divisors: 1 and themselves.

2. Another property of composite numbers is that they can be written as the product of two or more prime numbers. For example, the composite number 12 can be written as the product of the prime numbers 2 and 3 (2 x 3 = 6). This is known as the fundamental theorem of arithmetic.

It is also worth noting that there are an infinite number of composite numbers, just as there are an infinite number of prime numbers. This is because there is no upper limit on the size of composite numbers (or prime numbers), and there will always be more composite numbers (and prime numbers) to discover.

In conclusion, a composite number is not a prime number, and it can be determined using methods such as trial division or the Sieve of Eratosthenes. Composite numbers have several important properties, including the fact that they have at least two positive integer divisors and can be written as the product of two or more prime numbers. It is also worth noting that composite numbers play an important role in mathematics and have many applications in various fields. For example, in number theory, researchers often study the properties of composite numbers and how they can be used to solve problems.

One important application of composite numbers is in the field of cryptography, where they are used to create secure communication systems. Many encryption algorithms rely on the difficulty of factoring large composite numbers into their prime factors. This makes it difficult for unauthorized parties to intercept and decrypt messages. Composite numbers are also used in other areas of computer science, such as in the design of error-correcting codes and the creation of random number generators.

In addition, composite numbers are used in various practical applications, such as in the construction of buildings and other structures. Engineers and architects often use composite materials, which are made up of two or more different materials, to create strong and lightweight structures. Overall, composite numbers are an important and fascinating aspect of mathematics that have numerous applications in various fields. Their properties and uses continue to be studied and explored by researchers and practitioners alike.