What is a non-linear data structure?
Data Structure
A data structure is a special way of organizing the data elements into a particular form. The arrangement of data in a particular order is very important to access the particular data element in less time easily without putting much effort.
For example, in our daily life, when we used to put our clothes in a particular drawer properly, especially in a sequence so that whenever we want to wear a particular dress, we may not require to suffer in finding it out, and save our time from wasting.
Similarly in this way, the computer system organizes the data in a particular specific manner, so that to access any particular data element, or to delete it or any other operation we require to perform on it, can be done easily without making many efforts and also it will be done in less time.
We can even further do the arrangements of the data elements entered into the data structure like sorting the elements in ascending or descending order.
Types of Data Structure
The Data structures are categorized on two bases:
- Primitive data structures
- Non-Primitive data structure
Let us look at what it is and how it derives non-linear data structures.
1. Primitive data structures
The primitive data structures are nothing but the predefined data structures, which are already defined; we do not require giving a particular definition. To derive the non-primitive data structures, we will use these primitive data structures to easily collect a large amount of data. These data structures involve int, float, char, etc. The ' int 'is a data type used to set the type of our data as an integer type; similarly, in this way, we have a float for assigning the type float to our data used to store the decimal values and so on.
2. Non-Primitive data structures
The non-primitive data structures are nothing but the defined data structures used to create particular data structures by using the primitive data structures. It is mainly used to store the collection of elements; it may be of the same data types and may differ depending on the program's need. In non - primitive data structures, we have a concept of Abstract data type. It is a derived data type that the user derives, and the user defines that data type. We must create an abstract data type for using it in many places. There are various non-primitive data structures like an array, linked list, queue, stack, etc.
Types of Non-primitive data structures
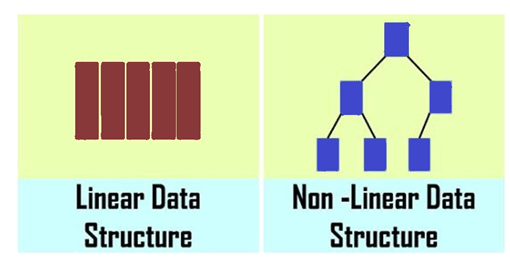
Now let us look at the linear and non-linear data structure briefly.
Linear Data structure:
- The linear data structure is nothing but arranging the data elements linearly one after the other. Here, we cannot arrange the data elements randomly as in the hierarchical order.
- This linear data structure will follow the sequential order of inserting the various data elements. Similarly, in this way, we perform the deletion operation onto the elements. Linear data structures are easy to implement because computer memory is arranged linearly. Its examples are array, stack, queue, linked list, etc.
Let us discuss some of its types:
Array:
- An array is a collection of homogeneous data elements consisting of mainly the same data types.
- An array consists of similar types of data elements present on the contiguous memory locations. Here the word contiguous means consecutive address locations. Suppose our particular array is starting from the address location 1000. Depending on its type, the next element is present at the consecutive memory location with the data type's difference in size.
Stack:
- Stack is also one of the important linear data structures based on the LIFO ( Last In First Out ) principle. Many computer applications and the various strategies used in the operating system and other places are based on the principle of LIFO itself. In this principle, the data element entered last must be popped out first from it, and the element pushed into the stack at the very first time is popped out last. In this approach, we will push the data elements into the stack until it reaches their end limit; after that, we will pop out the corresponding values.
Queue:
- A queue is one of the important linear data structures extensively used in various computer applications, and also it is based on the FIFO ( First In First Out ) principle. It follows a particular order of data execution for which operations are performed. In this data structure, data enters from one end, i.e., the REAR end, and the next data enters the queue after the previous one. Deletion operation is performed from another end, i.e., FRONT
Linked list:
- The linked list is another major data structure used in various programs, and even many non-linear data structures are implemented using this linked list data structure. As the name suggests, it consists of a link of the node connected by holding the address of the next node. It comes in the portion of the linear data structure because it forms the link-like structure the one data node is connected sequentially with the other node by carrying the address of that node.
- This data is not arranged in a sequential contiguous location as observed in the array. The homogeneous data elements are placed at the contiguous memory location to retrieve data elements is simpler.
Now, let's start with non-linear data structures. Here, we will also discuss the coding part in detail.
Non-linear data structure
- A non-linear data structure is another important type in which data elements are not arranged sequentially; mainly, data elements are arranged in random order without forming a linear structure.
- Data elements are present at the multilevel, for example, tree.
- In trees, the data elements are arranged in the hierarchical form, whereas in graphs, the data elements are arranged in random order, using the edges and vertex.
- Multiple runs are required to traverse through all the elements completely. Traversing in a single run is impossible to traverse the whole data structure.
- Each element can have multiple paths to reach another element.
- The data structure where data items are not organized sequentially is called a non-linear data structure. In other words, data elements of the non-linear data structure could be connected to more than one element to reflect a special relationship among them.
Let us discuss some of its types:
Trees and Graphs are the types of non-linear data structures.
Tree:
- The tree is a non-linear data structure that is comprised of various nodes. The nodes in the tree data structure are arranged in hierarchical order.
- It consists of a root node corresponding to its various child nodes, present at the next level. The tree grows on a level basis, and root nodes have limited child nodes depending on the order of the tree.
- For example, in the binary tree, the order of the root node is 2, which means it can have at most 2 children per node, not more than it.
- The non-linear data structure cannot be implemented directly, and it is implemented using the linear data structure like an array and linked list.
- The tree itself is a very broad data structure and is divided into various categories like Binary tree, Binary search tree, AVL trees, Heap, max Heap, min-heap, etc.
- All the types of trees mentioned above differ based on their properties.
Graph
- A graph is a non-linear data structure with a finite number of vertices and edges, and these edges are used to connect the vertices.
- The graph itself is categorized based on some properties; if we talk about a complete graph, it consists of the vertex set, and each vertex is connected to the other vertexes having an edge between them.
- The vertices store the data elements, while the edges represent the relationship between the vertices.
- A graph is very important in various fields; the network system is represented using the graph theory and its principles in computer networks.
- Even in Maps, we consider every location a vertex, and the path derived between two locations is considered edges.
- The graph representation's main motive is to find the minimum distance between two vertexes via a minimum edge weight.
Properties of Non-linear data structures
- It is used to store the data elements combined whenever they are not present in the contiguous memory locations.
- It is an efficient way of organizing and properly holding the data.
- It reduces the wastage of memory space by providing sufficient memory to every data element.
- Unlike in an array, we have to define the size of the array, and subsequent memory space is allocated to that array; if we don't want to store the elements till the range of the array, then the remaining memory gets wasted.
- So to overcome this factor, we will use the non-linear data structure and have multiple options to traverse from one node to another.
- Data is stored randomly in memory.
- It is comparatively difficult to implement.
- Multiple levels are involved.
- Memory utilization is effective.
What is Tree Data structure?
Trees: Unlike Arrays, Stack, Linked Lists, and queues, which are linear data structures, trees are hierarchical.
- A tree data structure is a collection of objects or entities known as nodes linked together to represent or simulate hierarchy.
- This data is not arranged in a sequential contiguous location like as we have observed in an array, the homogeneous data elements are placed at the contiguous memory location so that the retrieval of data elements is simpler.
- A tree data structure is non-linear because it does not store sequentially. It is a hierarchical structure as elements in a Tree are arranged in multiple levels.
- The topmost node in the Tree data structure is known as a root node. Each node contains some data, and data can be of any type. The node contains the employee's name in the tree structure, so the data type would be a string.
- Each node contains some data and the link or reference of other nodes that can be called children.
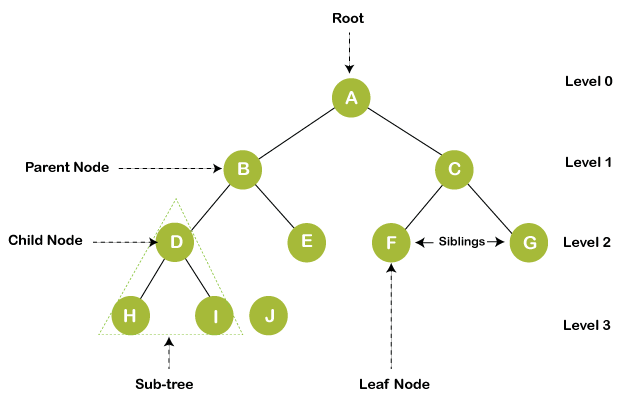
Terminologies used in tree:
- Root node: The tree consists of a root node; it is the starting node of the tree from which any tree grows. The root node is present at level 0 in any tree. Depending on the order of the tree, it can hold that much of child nodes. For example, if in a tree the order is 3, then it can have at most three child nodes, and minimum, it can have 0 child nodes.
- Child node: The child node is the node that comes after the root node, which has a parent node and has some ancestors. It is the node present at the next level of its parent node. For example, if any node is present at level 5, it is sure that its parent node is present at level 4, just above its level.
- Edge: Edges are nothing but the link between the parent node, and the children node is called the link or edge connectivity between two nodes.
- Siblings: The nodes having the same parent node is called siblings of each other. Same ancestors are not siblings, and only the parent node must be the same, defined as siblings. For example, if node A has two child nodes, B and C, B and C are called siblings.
- Leaf node: The leaf node is the node that does not have any child nodes. It is the termination point of any tree. It is also known as External nodes.
- Internal nodes: Internal nodes are non-leaf nodes, having at least one child node with child nodes.
- Degree of a node: The degree of a node is defined as the number of children nodes. The degree of the leaf node is always 0 because it does not have any children, and the internal node always has atleast one degree, as it contains atleast one child node.
- Height of the tree: The tree's height is defined as the distance of the root node to the leaf node present at the last level is called the height of the tree. In other words, height is the maximum level upto which the tree is extended.
Types of trees
Trees are divided into various categories as follows mentioned below:
- Simple Tree
- Binary tree
- Complete Binary tree
- Full Binary tree
- Binary search tree
- AVL Trees
- B -Tree
- B+ Tree
And many more.
Let us discuss a few of its types:
1. Simple tree - Simple tree is s nothing but an N - array tree consisting of a root node and having multiple child nodes. The child nodes are present on the next level root node, and in this, the tree grows. We do not have any restrictions on the root node's children; we can it a simple tree. Any tree with a hierarchical structure can be described as a general tree. A general tree is characterized by the lack of any configuration or limitations on the number of children a node can have. A node can have any number of children, and the tree's orientation can be any combination of these. The degree of the nodes can range from 0 to n.
2. Binary tree - It is a very important subcategory of simple trees. As the name suggests, we can easily predict that the binary tree is consists of two children only. A binary tree comprises nodes that can have two children, as described by the word "binary," which means "two numbers." Any node can have a maximum of 0, 1, or 2 nodes in a binary tree. Data structures' binary trees are highly functional ADTs that can be subdivided into various types.
A tree whose elements have at most 2 children is called a binary tree. Since each element in a binary tree can have only 2 children, we typically name them the left and right children. They are most commonly used in data structures for two reasons:
For obtaining nodes and categorizing them, as observed in Binary Search Trees.
For representing data through a bifurcating structure.
3. A Binary Search Tree (BST) is a subtype of a binary tree organized in such a way that the left subnode of the parent node is always less than the parent node, and the right subnode of the parent node is always greater than the parent node. Similarly in this way the whole tree grows, it is the modified version of the binary tree. In binary search tree, we have more restrictions as compared to the binary; in a binary tree, we have to maintain the 0, 1, or 2 children of every node, but here in this it is a binary tree, along with it, it must have some order in which insertion of child nodes is present. In BST, the right child is always less than the root node, and similarly, in this way, the left child is larger than the root node. In this, we will categorize the Binary search tree.
4. Complete Binary Tree: The complete binary tree is another form of the binary tree that consists of at most two children; it contains 0 or two children. The insertion of the nodes in the complete binary tree is always done from the left to right side.
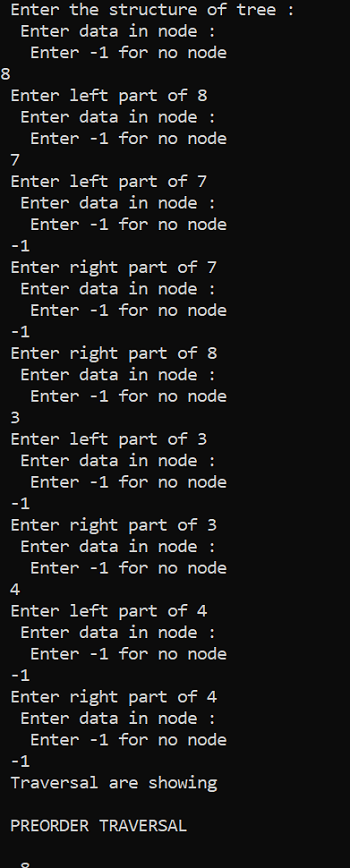
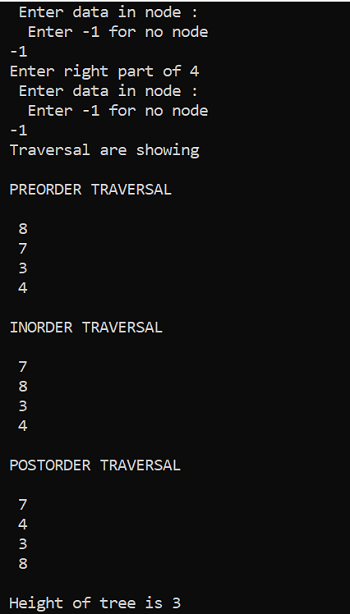
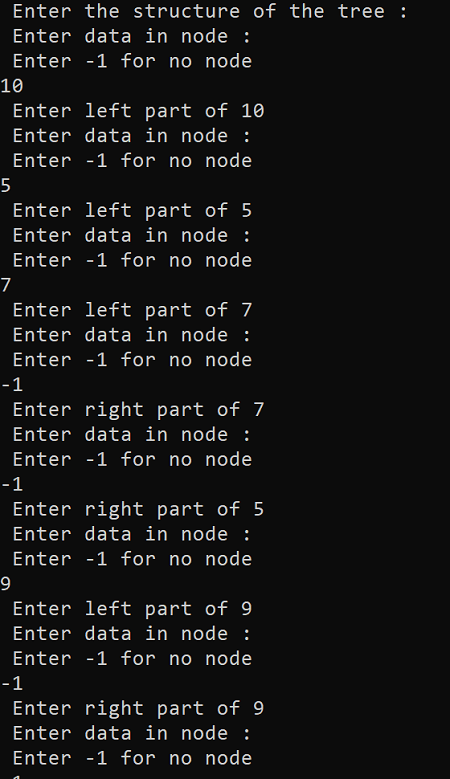
Binary tree implementation in C programming language -
The output of the above program
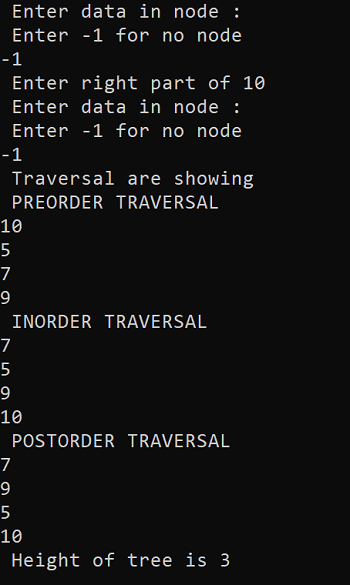
Binary tree implementation in C++ programming language -
The output of the above program
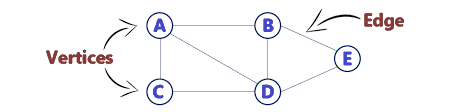
Graphs
- One node is connected with another node with an edge in a graph. The graph is a non-linear data structure consisting of nodes and edges and is represented by G ( V, E ), where V stands for the set of vertices and E stands for the set of edges. The graphs are divided into various categories: directed, undirected, weighted and unweighted, etc.
- This data is not arranged in sequential contiguous locations as observed in the array. The homogeneous data elements are placed at the contiguous memory location to retrieve data elements is simpler.
- It does not have any concept of root node or child node, unlike trees. Also, it does not have any particular order of arranging the data elements like in trees, and we have a particular hierarchical order in which the data elements are arranged.
- Every tree is called a graph, and in other words, we call it a spanning tree, which has the n-1 edges, where n stands for the total number of vertices in a graph.
Terminologies used in the graph:
- Vertex: The data element is represented using the vertex of the graph. There is one individual vertex for a particular data element to hold a data element.
- Edge: Edges are the connecting link between two vertex nodes; it is the traversing path from one vertex node to another.
- Undirected Edge: An undirected edge is an edge between the two vertexes having no direction; it is directed for both the vertexes, which means it is a bidirectional edge.
- Directed edge: Directed edge is the edge between the two vertexes having a particular direction from one node to another node.
- Weighted edge: The edge which consists of a particular value over it, which we call a weight of the particular edge for traversing it from one vertex to the other. The weighted edges are important in finding the minimum path from one node to another.
- Degree: The degree of the vertex is defined as the total number of edges connected to that vertex.
- Indegree: The indegree of a vertex is defined as the total number of edges coming to the particular vertex.
- Outdegree: The outdegree of a vertex is defined as the total number of edges outgoing from that vertex.
Types of Graph:
- Trivial graph
- Directed Graph
- Undirected graph
- Weighted graph
- Simple graph
- Multigraph
- Null graph
- Complete graph
Let us discuss some of its types are:
1. Trivial graph: We have only a single vertex in a trivial graph, and this vertex does not have any edge.
2. Directed Graph: The graph consists of a directed set of edges in which every edge is associated with a particular direction. These directing edges direct the direction of the path from one vertex to another.
3. Undirected graph: The graph consists of an undirected set of edges, in which every edge is connected with the vertexes but does not specify a particular direction.
4. Weighted graph: The weighted graph is the graph that consists of the edges having some weights over them; it means edges consist of some value for going from one vertex to the other.
5. Simple graph: Simple graph is defined as a graph that consists of only one edge between the two vertexes. Simple graphs do not consist of any parallel edges and self-loops.
6. Multigraph: Multigraph consists of parallel edges and self-loops. It is more complex as compared to simple graphs.
7. Null graph: Null graph consists of an empty set of edges, in which the vertex set does not contain any edges connecting between them.
8. Complete graph: Complete graph is how each vertex is connected with every other vertex. In a complete graph, each vertex's degree must be n - 1, where n is denoted as the number of vertices.
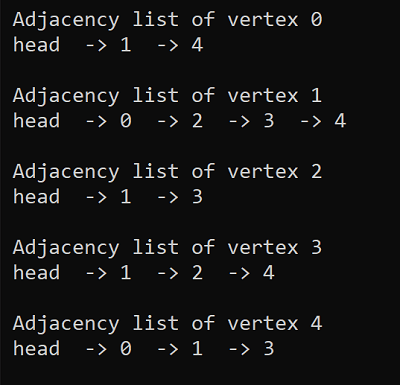
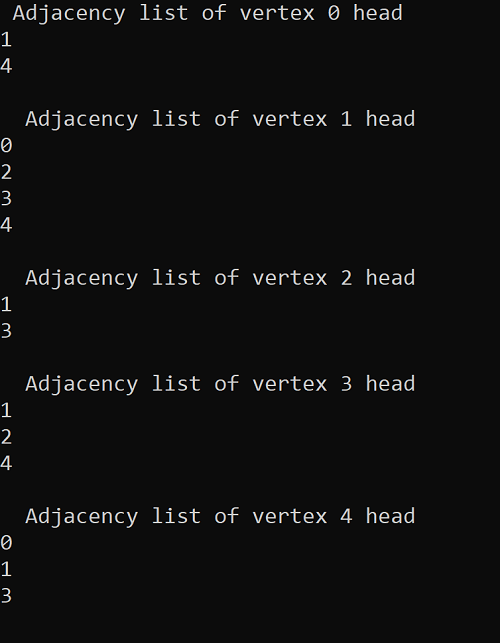
Graph implementation in C programming language -
The output of the above program
Graph implementation in C++ programming language -
The output of the above program
|









 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now










