What is the formula for PerimeterPerimeter refers to a continuous line that configures a boundary of a closed geometrical shape. The word perimeter is taken from two Greek words: "Peri" means around, and "metron" means measure. The unit of Perimeter is the same as distance meter, feet, miles, and inch. In this tutorial, we will discuss the Perimeter of various geometrical shapes. Perimeter of RectangleThe term "Rectangle" refers to a geometrical shape with four sides, with both opposite sides are of the same length. The Perimeter of a rectangle can be defined as the sum of the total length of all the sides. Method 1Calculating Perimeter with length and widthTo calculate the Perimeter of a rectangle, you need to recall the basic formula of a rectangle that you have studied in your school time. P = 2 × (l + W) Where P stands for Perimeter of the rectangle. l stands for the length of the rectangle. w stands for the Width of the rectangle. Perimeter is usually the sum of total distance around the outer edge of any shape, whether it is complex or straightforward. In a rectangle, the length is always greater than the width. Let's understand the concept with the help of an example; if the length of the rectangle is 12 cm and the width is 6 cm, find the Perimeter of the rectangle. 
Here, given length of the rectangle (l) = 12 cm Width of the rectangle(w) = 6 cm We know that the formula of the perimeter of the rectangle P = 2 × (l + W) = 2 × (12 + 6) = 2 × (18) = 36 Method 2Finding the Perimeter with Area and One side We know the formula of Area = (l + W) Where, Where A = Area. L = length of the rectangle. W = Width of the rectangle. Let's understand this concept with an example, if the area of a rectangle is 144 cm2 and the length of the rectangle is 12 cm, find the Perimeter of the rectangle. We know that, Area = (l + W) 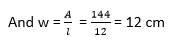
Now, The equation of the perimeter of a rectangle = P = 2 × (l + W) = 2 × (14 + 12) = 2 × (26) = 52 cm Perimeter of a SquareThe Perimeter of any two- dimensional shape is the total sum of the length of its side. Square is made up of four sides with equal length, and it makes four right angles. Since all the sides have equal lengths, we can easily calculate the Perimeter of the square. 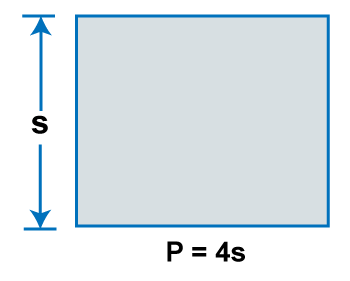
Method 1Finding the Perimeter when on side length is known As we know, the square has equal sides. if we consider each side of length s, the Perimeter of the square is simple four times the length that is P = 4s Where P stands for Perimeter of the square. S stands for sides of the square. Let's understand this concept with an example, if the length of the side of a square is 6, find the perimeter of the square. Given, length of the side of a square = 6 We know that, The perimeter of the square = 4s = 4 × 6 = 24 Method 2Finding the Perimeter of the square when Area is known The area of any rectangular shape is defined as the base times of its height. Since the base and height of the square is the same, so the area of a square with equal sides length s is given as 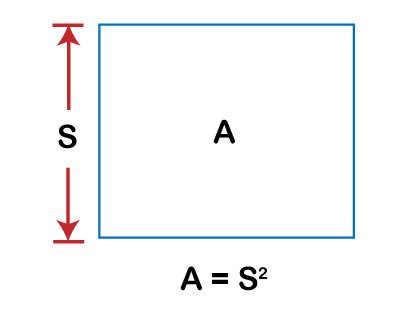
A = s×s = s2 Where A = Area of the square. S = sides of the square. Find the square root of the area. The square root of the area will give the length of the one side of the square. So, S = ?A Let's understand this concept with an example, if the area of a square is 36, find the side of the square. Given, Area of the square = 36 Side of the square =? We know that S = ?A S = ?36 = 6 We know that, The perimeter of the square = 4s = 4 × 6 = 24 Method 3Finding the Perimeter of a square inscribed in a circle of known radius. 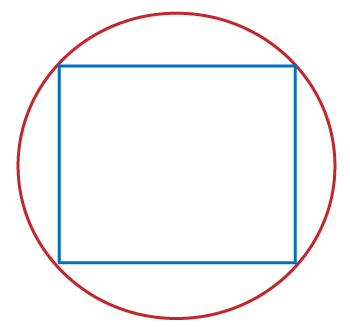
Understanding the inscribed square Many times, you find a square inscribed in a circle is a square that is drawn inside the circle, so all the corners line on the edge of the circle. Find the relation between the side of the length of the square and the radius of the circle. The circle's radius is equal to the distance from the center of an inscribed square to each of its vertices. To calculate the length of side s, you need first to suppose cutting the square in half diagonally to form two right-angle triangles. Each of the right-angle triangles will have equal sides p and q and hypotenuse t. We know that the hypotenuse of the right-angle triangle is equal to two times the radius of the circle 2r. 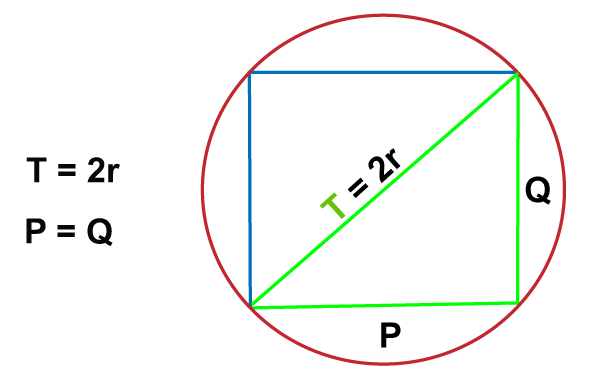
Apply the Pythagorean theorem to calculate the side length of the square. The Pythagorean theorem states that for any right-angle triangle with sides p and q and hypotenuse, t equals t2= p2 + q2. Since sides, p and q are equal in the square, and we know that t = 2r, we can simply write the equation and calculate the side length of the square t2= p2 + q2 p2 + p2 = (2r)2 2 p2 = 4 r2 Dividing both sides by 2, we get p2 = 2 r2 Now, taking the square root of both the sides, we get P = ?2 r2 = 2 r The side length is s for the inscribed square = 2 r To find the perimeter of the square, multiply the side length of the square by 4. Means Perimeter = 4?2 r Lets us understand the concept with an example. If a square is inscribed in a circle with a radius of 8, find the perimeter of the square. Given Radius r = 8 So, the diagonal of the square = 2(8) = 16 We know that Pythagorean theorem = 2 p2= 162 = 2 p2= 256 Now divide both side of the equation by 2 we get p2= 128 and, p = ?128 = 11.31. To find the perimeter of the square, we need to multiply the given value by 4 Perimeter = 11.31 × 4 = 45.25 Perimeter of the TriangleCalculating the Perimeter of the triangle means finding the total distance around the circle. The easiest method to find the Perimeter of the triangle is to add the total length of its sides, but if you don't know all of the side lengths first, you need to calculate the side. Method 1Calculating the Perimeter when three lengths of all the sides are known Remember the formula 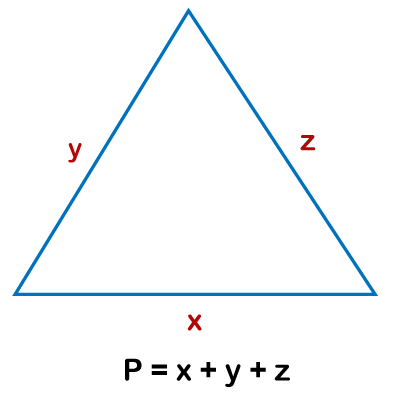
To find the perimeter of a triangle, you need to remember the formula. Suppose a triangle with sides x, y, and z; the perimeter P is defined as P = x + y + z Where, P = Perimeter x = side of tringle y = side of tringle z = side of tringle Lets us understand the concept with an example. If a triangle with sides x = 3, y = 4 and z = 5, find the perimeter of the tringle Given, Length of the sides of triangle x = 3 Length of the sides of triangle y = 4 Length of the sides of triangle z = 5 Therefore, the perimeter of the tringle = x + y + z = 3 + 4 + 5 = 12 Method 2Calculating the Perimeter of a right-angle triangle when only two sides are known Remember the right angle triangle. 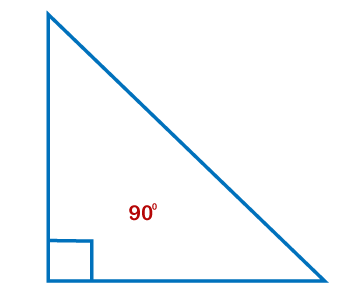
We know that a right-angle triangle refers to a triangle with one right angle, and the side of the triangle opposite to the right angle is always the longest side known as hypotenuse. Apply the Pythagorean theorem The Pythagorean theorem states that for any right-angle triangle with sides p and q and hypotenuse t is equals to z2= x2 + y2 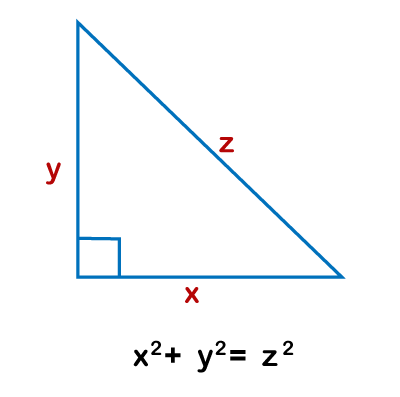
Put the side lengths into the Pythagorean theorem We know the Pythagorean theorem z2= x2 + y2 Let's understand this concept with the help of an example, suppose, a right-angle triangle with sides y = 3, q = 4, then find the hypotenuse? We know that, according to Pythagorean theorem z2= x2 + y2 Given, x = 3 And y = 4 So, z2= 32 + 42 = 9 + 16 = 25, z = 5 Sum up the length of the tree side lengths to calculate Perimeter Remember the perimeter formula that is Perimeter = x + y + z. Now we know the lengths of sides x,y,z; we simply need to sum up the length together to calculate the Perimeter. 3+4+5 = 12 Calculating the Perimeter of a circleFind the circumference of a circle Circumference refers to the total distance around the circle, and it is equal to its Perimeter. The formula is used to calculate the circumference C = 2 . r, where C stands for circumference and r stands for the radius of the circle. As we know that the radius is half of the diameter, we can use the formula C = (d) (You can use this formula when you have a diameter instead of radius). When calculating the Perimeter of a circle, never use the term perimeter; use circumference in place of Perimeter. (Because circles do not contain any straight line.) Put the value of the radius into the formula. In the formula of circumference, you need to put the value of variable r. Suppose, if the radius of the circle r is given 4 cm, your equation will look like 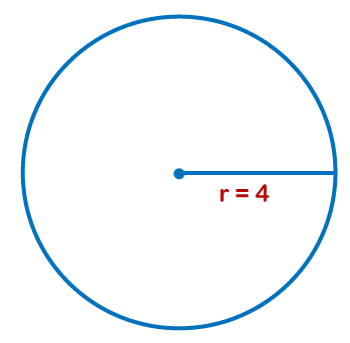

Find the Perimeter of the circle if the area of the circle is given. We know that the ^equation A=?r2 gives the area of the circle. So, if you put the area into the equation, you will get the value for r. Once you get the value of r, you can use the circumference formula to calculate the circumference. Let's understand with the help of an example, suppose the area of a circle is 81 square centimeters, find the circumference or perimeter of the circle. We know that, The formula of area of a circle A=?r^2. Here A stands of the area of the circle is given 81 square centimeters. ?= 3.14 R = radius of the circle. Therefore, 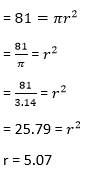
We know that, circumference or perimeter of the circle C = 2? . r C = 2? . 5.07 C = 31.83 So, the circumference of the circle equals 31.83 Calculating the Perimeter of a PentagonFind the number of sides and the length of one side. 
As the name suggests, Pentagon has five sides, so you need to put five into the equation. After that, you need to calculate the length of one side to put in for the variable. Put the variable into the formula. The equation to calculate the Perimeter of a pentagon is P = 5 × s. Where P stands for Perimeter. And s stands for the length of 1 side. Suppose the length of the one side of the pentagon is 4; you will get the result. P = 5 × 4. = 20 Calculating the Perimeter of a Regular PolygonFind the length of the one side of the polygon 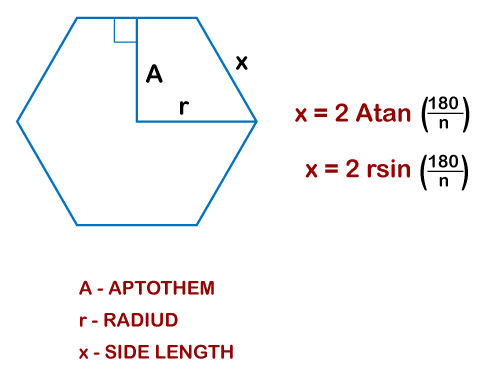
A regular polygon refers to a polygon that is equilateral and equiangular. If you know the radius of the polygon, you can find the length of one side. The radius of the polygon refers to the distance between the center of the polygon and any vertex. The given formula is used to find the side length when the radius is known 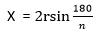
Where, X is the same as the side length, and r equals radius. The given formula is used to find the side length when apothem is known 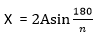
Where, X is the same as the side length, and A equals apothem. Let's consider an example to find the sidle length. Suppose the radius of the hexagon is 8 cm; find its side length. We know that, 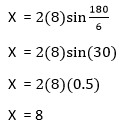
Example: If the radius of the hexagon is 10 cm, find its side length? We know that, 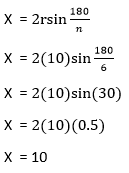
Find the formula for the perimeter of a regular polygon. The formula for the perimeter of a regular polygon is P = nx Where, N stands for the number of sides the polygon has X stands for the length of one side of the polygon. Put the values of x and n into the formula. We have already calculated the value of x and n, so we need to multiply these values to calculate the Perimeter of the polygon. 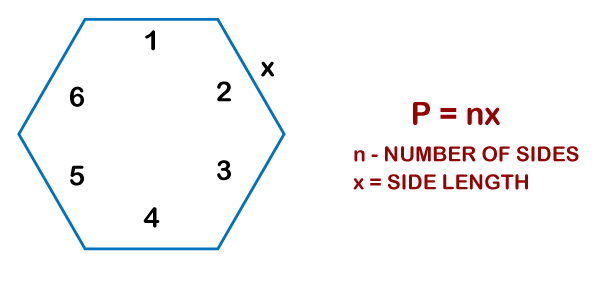
Let's consider an example to find the perimeter of a regular hexagon. Suppose the hexagon has a side length of 8 cm, then find the perimeter of the regular hexagon. Given, number of sides, the polygon n = 6 length of one side of the polygon x = 8 We know the formula for the perimeter of a regular polygon is P = nx P = (6)(8) = 48 Example: If the hexagon has a side length of 10 cm, then find the perimeter of the regular hexagon Given, number of sides, the polygon n = 6 length of one side of the polygon x = 10 We know the formula for the perimeter of a regular polygon is P = nx P = (6)(10) = 60 Determining the Perimeter of a QuadrilateralCalculate the length of all four sides We know that the shape of the quadrilateral looks the same as a rectangle with uneven sides. You can easily calculate the Perimeter once you know the four sides of the quadrilateral by adding them all. 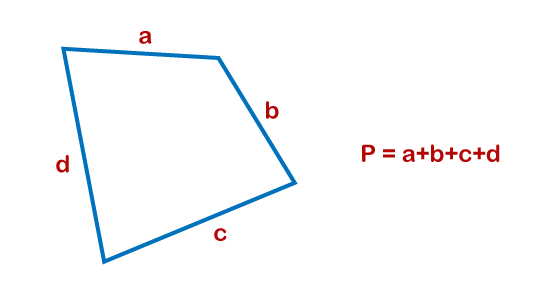
In case the length of the four sides of the quadrilateral is not given, you can use the data you do have to find for variable x Let's consider an example to find the Perimeter of a quadrilateral. Suppose the quadrilateral has a side length of a = 3cm, b = 4cm, c= 6cm, and d = 8 cm, then find the perimeter of the quadrilateral. We know that, the formula to calculate the perimeter of a quadrilateral P = a + b + c + d = 3 + 4 + 6 + 8 = 21 Example: If the quadrilateral has a side length of a = 6 cm, b = 7cm, c= 9cm, and d = 11 cm, find the quadrilateral's perimeter. We know that, the formula to calculate the perimeter of a quadrilateral P = a + b + c + d = 6 + 7 + 9 + 11 = 33 Calculating the Perimeter of an EllipseMeasure the side of the ellipse An ellipse refers to an oval-shaped circle, so it does not contain any straight lines. If you want to calculate the ellipse's perimeter, you need to know the circumference of both the width and the height. If you don't know the value, you need to measure the ellipse. Usually, variables p goes from the left to right on the major axis, and variable q goes up and sown on the minor axis. 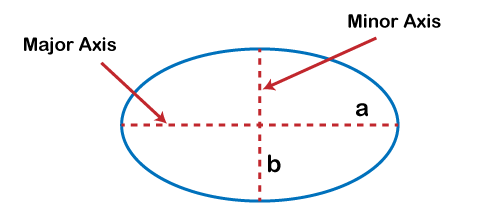
Apply the perimeter formula to calculate the Perimeter of the ellipse You can find the Perimeter of an ellipse using various equations. The formula primarily used to calculate the Perimeter of the ellipse is given below 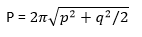
Let's consider an example to find the Perimeter of an ellipse. Suppose, if the variable p is six and variable q is 8, find the perimeter of the ellipse? We know that the formula to calculate the Perimeter of an ellipse 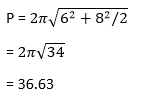
Calculating the Perimeter of a sectorDetermine the length of the arc A sector refers to a triangular part taken from the circle. If you want to find the length of the arc, you need to find the length or variable l. 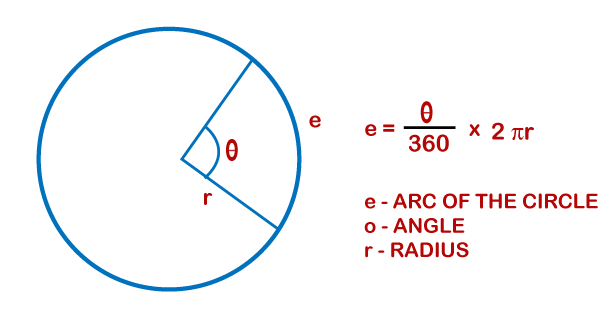
You can find the length with the help of the given equation 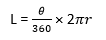
Where, L = Arc of the circle ? = angle of the sector r = Radius Put the variables into the equation To calculate the Perimeter of a sector, put the above value in the equation, we get 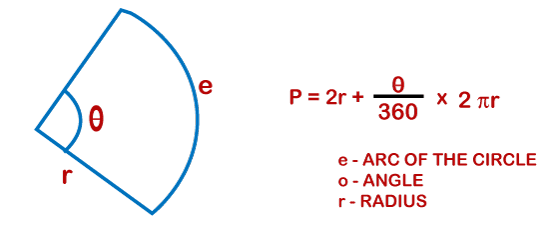
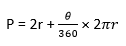
Where, 2r stands for two times the radius ?= angle of the sector Let's consider an example to understand this concept. Suppose the value of a radius of a sector is 3, and the angle made by the sector is 600; find the Perimeter of the sector? Given, r = 3 We know that, 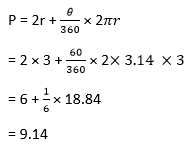
Example If the radius of a sector is 5, and the angle made by the sector is 400 find the Perimeter of the sector? Given, The radius of a sector r = 5 Angle made by the sector ?= 400 We know that, 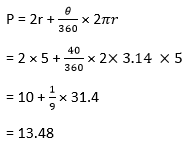
Next TopicGraphs Examples
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










