Whole Number

All positive integers from zero to eternity are enclosed within the cluster of numbers called whole numbers. The quantity line has these numbers. They're all real numbers, as a result. Though not all real numbers are whole numbers, we can that every whole number are real numbers. As a result, the set of natural numbers and zero may be accustomed to outline whole numbers. The class of whole numbers and, therefore, the negative of natural numbers are understood as integers. Thus, integers may be either positive or negative, together with zero. Natural numbers, whole numbers, integers, and fractions all constitute the class of real numbers.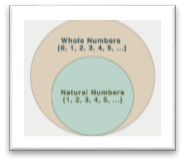

Whole numbers include all-natural numbers, together with '0' in their entireness. These are some examples: zero, 11, 25, 36, 999, 1200, etc.

Properties of Whole Numbers

Arithmetic operations like addition, subtraction, division, and multiplication measure the inspiration of the properties of whole numbers. An entire variety can result from the addition or multiplication of two whole numbers. Once two whole numbers square measure deducted, the result won't be an entire number; instead, it would be a number. In some instances, the division of two whole numbers yields a fraction.

1. Closure Property

If two whole numbers, x and y, are presented, they'll be closed by addition and multiplication, which means that x.y or x + y is also a whole number.

Example:

Whole numbers 5 and 8

5 + 8 = 13 is also a whole number

5 x 8 = 40 is also a whole number

Thus, in addition and multiplication, complete whole numbers are formed.

2. Commutative property of addition and multiplication

Two whole numbers can continually add up to at least one another or multiply along within the same method; thus, if x and y are two whole numbers, then x + y = y + x and x.y = y. x

Example:

Consider two whole numbers, 3 and 7.

3 + 7 = 10

7 + 3 = 10

Thus, 3 + 7 = 7 + 3.

Also,

3 × 7 = 21

7 × 3 = 21

Thus, 3 × 7 = 7 × 3

Therefore, addition and multiplication units are independent of whole integers.

3. Additive identity

If x may be an integer, then x + zero = zero + x = x. This is often because once an entire range is accessorial to zero, its value doesn't support the amendment.

Example:

Consider two whole numbers, 0 and 11.

0 + 11 = 11

11 + 0 = 11

Here, 0 + 11 = 11 + 0 = 11

Since zero is the additive identity of all whole numbers, this is often why the value of whole number is not impacted.

4. Multiplicative identity

A whole range has no impact once it's increased by one; therefore, if x could be a number, then x.1 = x = 1.x.

Example:

Think about the numbers 1 and 15.

1 × 15 = 15

15 × 1 = 15

Here, 1 × 15 = 15 = 15 × 1

The increasing identity of whole numbers is one reason for this.

5. Associative property

If x, y, and z are all whole numbers, then x + (y + z) = (x + y) + z and x. (y.z) = (x.y).z can all turn out constant results once the entire numbers are decreased or increased as a group.

For example:

Consider three whole numbers 2, 3, and 4.

2 + (3 + 4) = 2 + 7 = 9

(2 + 3) + 4 = 5 + 4 = 9

Thus, 2 + (3 + 4) = (2 + 3) + 4

2 × (3 × 4) = 2 × 12 = 24

(2 × 3) × 4 = 6 × 4 = 24

Here, 2 × (3 × 4) = (2 × 3) × 4

Facts of the whole number

• Whole numbers make up all natural numbers.
• There are only whole numbers when counting.
• Whole numbers are made up of zero and all positive integers.
• Real numbers are all entire numbers.

Some Questions Related to Whole Numbers

1. Can the entire range have a negative value?

A complete range can't be negative, so the solution isn't any. Whole numbers are expressed as 0, 1, 2, 3, and then 4. They are regarded to be whole numbers, and not all whole numbers are thought-about to be natural numbers. Negative numbers are thus not thought to be entire numbers.

2. Give an explanation of whole numbers.

Integers that are positive and embrace zero are said as whole numbers. A full range has no fraction or decimal. This implies that while not the bits, it represents the whole entity. The mathematical illustration of the set of whole numbers is: 0, 1, 2, 3, etc.

3. Which range falls outside the variety of whole numbers?

The numbers between zero and eternity that don't exist aren't whole numbers, as stated. Rational numbers, negative integers, and fractions aren't whole numbers. Samples of non-whole numbers are -1, -5, 12, 9/4, etc.

4. Is the range "10" the best number?

10 could be a {natural range number} and an ideal number. There are unit 10 words in it. However, -10 conjointly stands for a full, not a fraction.