Fuzzy Logic Tutorial

What is Fuzzy Logic?

The 'Fuzzy' word means the things that are not clear or are vague. Sometimes, we cannot decide in real life that the given problem or statement is either true or false. At that time, this concept provides many values between the true and false and gives the flexibility to find the best solution to that problem.

Example of Fuzzy Logic as comparing to Boolean Logic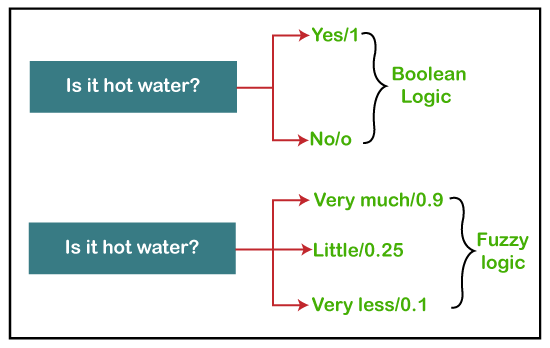

Fuzzy logic contains the multiple logical values and these values are the truth values of a variable or problem between 0 and 1. This concept was introduced by Lofti Zadeh in 1965 based on the Fuzzy Set Theory. This concept provides the possibilities which are not given by computers, but similar to the range of possibilities generated by humans.

In the Boolean system, only two possibilities (0 and 1) exist, where 1 denotes the absolute truth value and 0 denotes the absolute false value. But in the fuzzy system, there are multiple possibilities present between the 0 and 1, which are partially false and partially true.

The Fuzzy logic can be implemented in systems such as micro-controllers, workstation-based or large network-based systems for achieving the definite output. It can also be implemented in both hardware or software.

Characteristics of Fuzzy Logic

Following are the characteristics of fuzzy logic:

1. This concept is flexible and we can easily understand and implement it.
2. It is used for helping the minimization of the logics created by the human.
3. It is the best method for finding the solution of those problems which are suitable for approximate or uncertain reasoning.
4. It always offers two values, which denote the two possible solutions for a problem and statement.
5. It allows users to build or create the functions which are non-linear of arbitrary complexity.
6. In fuzzy logic, everything is a matter of degree.
7. In the Fuzzy logic, any system which is logical can be easily fuzzified.
8. It is based on natural language processing.
9. It is also used by the quantitative analysts for improving their algorithm's execution.
10. It also allows users to integrate with the programming.

Architecture of a Fuzzy Logic System

In the architecture of the Fuzzy Logic system, each component plays an important role. The architecture consists of the different four components which are given below.

1. Rule Base
2. Fuzzification
3. Inference Engine
4. Defuzzification

Following diagram shows the architecture or process of a Fuzzy Logic system: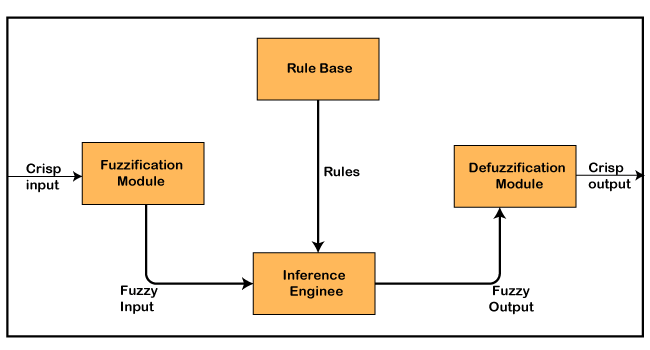

1. Rule Base

Rule Base is a component used for storing the set of rules and the If-Then conditions given by the experts are used for controlling the decision-making systems. There are so many updates that come in the Fuzzy theory recently, which offers effective methods for designing and tuning of fuzzy controllers. These updates or developments decreases the number of fuzzy set of rules.

2. Fuzzification

Fuzzification is a module or component for transforming the system inputs, i.e., it converts the crisp number into fuzzy steps. The crisp numbers are those inputs which are measured by the sensors and then fuzzification passed them into the control systems for further processing. This component divides the input signals into following five states in any Fuzzy Logic system:

• Large Positive (LP)
• Medium Positive (MP)
• Small (S)
• Medium Negative (MN)
• Large negative (LN)

3. Inference Engine

This component is a main component in any Fuzzy Logic system (FLS), because all the information is processed in the Inference Engine. It allows users to find the matching degree between the current fuzzy input and the rules. After the matching degree, this system determines which rule is to be added according to the given input field. When all rules are fired, then they are combined for developing the control actions.

4. Defuzzification

Defuzzification is a module or component, which takes the fuzzy set inputs generated by the Inference Engine, and then transforms them into a crisp value.  It is the last step in the process of a fuzzy logic system. The crisp value is a type of value which is acceptable by the user. Various techniques are present to do this, but the user has to select the best one for reducing the errors.

Membership Function

The membership function is a function which represents the graph of fuzzy sets, and allows users to quantify the linguistic term. It is a graph which is used for mapping each element of x to the value between 0 and 1.

This function is also known as indicator or characteristics function.

This function of Membership was introduced in the first papers of fuzzy set by Zadeh. For the Fuzzy set B, the membership function for X is defined as: μB:X → [0,1]. In this function X, each element of set B is mapped to the value between 0 and 1. This is called a degree of membership or membership value.

Classical and Fuzzy Set Theory

To learn about classical and Fuzzy set theory, firstly you have to know about what is set.

Set

A set is a term, which is a collection of unordered or ordered elements. Following are the various examples of a set:

1. A set of all-natural numbers
2. A set of students in a class.
3. A set of all cities in a state.
4. A set of upper-case letters of the alphabet.

Types of Set:

There are following various categories of set:

1. Finite
2. Empty
3. Infinite
4. Proper
5. Universal
6. Subset
7. Singleton
8. Equivalent Set
9. Disjoint Set

Classical Set

It is a type of set which collects the distinct objects in a group. The sets with the crisp boundaries are classical sets. In any set, each single entity is called an element or member of that set.

Mathematical Representation of Sets

Any set can be easily denoted in the following two different ways:

1. Roaster Form: This is also called as a tabular form. In this form, the set is represented in the following way:

The elements in the set are enclosed within the brackets and separated by the commas.

Following are the two examples which describes the set in Roaster or Tabular form:

Example 1:

Example 2:

2. Set Builder Form: Set Builder form defines a set with the common properties of an element in a set. In this form, the set is represented in the following way:

The following example describes the set in the builder form:

Operations on Classical Set

Following are the various operations which are performed on the classical sets:

1. Union Operation
2. Intersection Operation
3. Difference Operation
4. Complement Operation

1. Union:

This operation is denoted by (A U B). A U B is the set of those elements which exist in two different sets A and B. This operation combines all the elements from both the sets and make a new set. It is also called a Logical OR operation.

It can be described as:

Example:

2. Intersection

This operation is denoted by (A ∩ B). A ∩ B is the set of those elements which are common in both set A and B. It is also called a Logical OR operation.

It can be described as:

Example:

3. Difference Operation

This operation is denoted by (A - B). A-B is the set of only those elements which exist only in set A but not in set B.

It can be described as:

4. Complement Operation: This operation is denoted by (A`). It is applied on a single set. A` is the set of elements which do not exist in set A.

It can be described as:

Properties of Classical Set

There are following various properties which play an essential role for finding the solution of a fuzzy logic problem.

1. Commutative Property:

This property provides the following two states which are obtained by two finite sets A and B:

2. Associative Property:

This property also provides the following two states but these are obtained by three different finite sets A, B, and C:

3. Idempotency Property:

This property also provides the following two states but for a single finite set A:

4. Absorption Property

This property also provides the following two states for any two finite sets A and B:

5. Distributive Property:

This property also provides the following two states for any three finite sets A, B, and C:

6. Identity Property:

This property provides the following four states for any finite set A and Universal set X:

7. Transitive property

This property provides the following state for the finite sets A, B, and C:

8. Ivolution property

This property provides following state for any finite set A: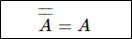

9. De Morgan's Law

This law gives the following rules for providing the contradiction and tautologies: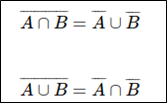

Fuzzy Set

The set theory of classical is the subset of Fuzzy set theory. Fuzzy logic is based on this theory, which is a generalisation of the classical theory of set (i.e., crisp set) introduced by Zadeh in 1965.

A fuzzy set is a collection of values which exist between 0 and 1. Fuzzy sets are denoted or represented by the tilde (~) character. The sets of Fuzzy theory were introduced in 1965 by Lofti A. Zadeh and Dieter Klaua. In the fuzzy set, the partial membership also exists. This theory released as an extension of classical set theory.

This theory is denoted mathematically asA fuzzy set (Ã) is a pair of U and M, where U is the Universe of discourse and M is the membership function which takes on values in the interval [ 0, 1 ]. The universe of discourse (U) is also denoted by Ω or X.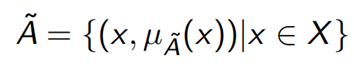

Operations on Fuzzy Set

Given à and B are the two fuzzy sets, and X be the universe of discourse with the following respective member functions: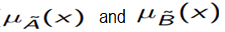

The operations of Fuzzy set are as follows:

1. Union Operation: The union operation of a fuzzy set is defined by:

μA∪B(x) = max (μA(x), μB(x))

Example:

Let's suppose A is a set which contains following elements:

And, B is a set which contains following elements:

then,

Because, according to this operation

For X₁

For X₂

For X₃

For X₄

2. Intersection Operation:The intersection operation of fuzzy set is defined by:

μA∩B(x) = min (μA(x), μB(x))

Example:

Let's suppose A is a set which contains following elements:

And, B is a set which contains following elements:

then,

Because, according to this operation

For X₁

For X₂

For X₃

For X₄

3. Complement Operation: The complement operation of fuzzy set is defined by:

μĀ(x) = 1-μA(x),

Example:

Let's suppose A is a set which contains following elements:

then,

Because, according to this operation

For X₁

For X₂

For X₃

For X₄

Applications of Fuzzy Logic

Following are the different application areas where the Fuzzy Logic concept is widely used:

1. It is used in Businesses for decision-making support system.
2. It is used in Automative systems for controlling the traffic and speed, and for improving the efficiency of automatic transmissions. Automative systems also use the shift scheduling method for automatic transmissions.
3. This concept is also used in the Defence in various areas. Defence mainly uses the Fuzzy logic systems for underwater target recognition and the automatic target recognition of thermal infrared images.
4. It is also widely used in the Pattern Recognition and Classification in the form of Fuzzy logic-based recognition and handwriting recognition. It is also used in the searching of fuzzy images.
5. Fuzzy logic systems also used in Securities.
6. It is also used in microwave oven for setting the lunes power and cooking strategy.
7. This technique is also used in the area of modern control systems such as expert systems.
8. Finance is also another application where this concept is used for predicting the stock market, and for managing the funds.
9. It is also used for controlling the brakes.
10. It is also used in the industries of chemicals for controlling the ph, and chemical distillation process.
11. It is also used in the industries of manufacturing for the optimization of milk and cheese production.
12. It is also used in the vacuum cleaners, and the timings of washing machines.
13. It is also used in heaters, air conditioners, and humidifiers.

Advantages of Fuzzy Logic

Fuzzy Logic has various advantages or benefits. Some of them are as follows:

1. The methodology of this concept works similarly as the human reasoning.
2. Any user can easily understand the structure of Fuzzy Logic.
3. It does not need a large memory, because the algorithms can be easily described with fewer data.
4. It is widely used in all fields of life and easily provides effective solutions to the problems which have high complexity.
5. This concept is based on the set theory of mathematics, so that's why it is simple.
6. It allows users for controlling the control machines and consumer products.
7. The development time of fuzzy logic is short as compared to conventional methods.
8. Due to its flexibility, any user can easily add and delete rules in the FLS system.

Disadvantages of Fuzzy Logic

Fuzzy Logic has various disadvantages or limitations. Some of them are as follows:

1. The run time of fuzzy logic systems is slow and takes a long time to produce outputs.
2. Users can understand it easily if they are simple.
3. The possibilities produced by the fuzzy logic system are not always accurate.
4. Many researchers give various ways for solving a given statement using this technique which leads to ambiguity.
5. Fuzzy logics are not suitable for those problems that require high accuracy.
6. The systems of a Fuzzy logic need a lot of testing for verification and validation.