Program to Convert Binary Tree to Binary Search Tree

Q. Program to convert Binary Tree to Binary Search Tree.

Explanation

In this program, we need to convert given binary tree to a corresponding binary search tree. A tree is said to be the binary tree if each of the nodes has at most two children. Whereas, the binary search tree is the special case of the binary tree in which all the nodes to the left of root node should be less than root node and nodes to the right should be greater than root node.

This problem can be resolved by converting given binary tree to its corresponding array representation. Sort the array. Calculate the middle node from array elements as it will become the root node of the corresponding binary search tree.

Program to convert Binary Tree to Binary Search Tree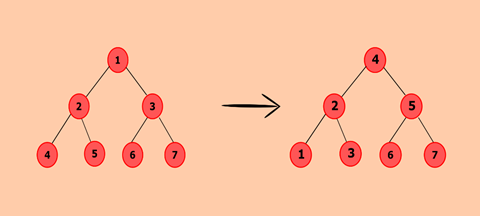

Algorithm

Define Node class which has three attributes namely: data left and right. Here, left represents the left child of the node and right represents the right child of the node.
When a node is created, data will pass to data attribute of the node and both left and right will be set to null.
Define another class which has two attribute root and treeArray.
1. Root represents the root node of the tree and initializes it to null.
2. treeArray will store the array representation of the binary tree.
convertBTBST() will convert binary tree to the corresponding binary search tree:
1. It will convert the binary tree to corresponding array by calling convertBTtoArray().
2. Sort the resultant array from step 1 in ascending order.
3. Convert the array to the binary search tree by calling createBST().
calculateSize() will count the number of nodes present in the tree.
convertBTtoArray() will convert binary tree to its array representation by traversing the tree and adding elements to treeArray.
createBST() will create a corresponding binary search tree by selecting a middle node of sorted treeArray as it the root node. treeArray will be divided into two parts i.e [0, mid-1] and [mid+1, end]. Recursively find middle node from each array to create left subtree and right subtree respectively.
Inorder() will display the nodes of the tree in inorder fashion, i.e., left child followed by root node followed by the right child.

Solution

Python

#Represent a node of binary tree
class Node:
    def __init__(self,data):
        #Assign data to the new node, set left and right children to None
        self.data = data;
        self.left = None;
        self.right = None;
 
class ConvertBTtoBST:
    def __init__(self):
        #Represent the root of binary tree
        self.root = None;
        self.treeArray = [];
        
    #convertBTBST() will convert a binary tree to the binary search tree
    def convertBTBST(self, node):
        
        #Converts binary tree to array
        self.convertBTtoArray(node);
        
        #Sort treeArray
        self.treeArray.sort();
        
        #Converts array to binary search tree
        d = self.createBST(0, len(self.treeArray) -1);
        return d;
        
    #convertBTtoArray() will convert the given binary tree to its corresponding array representation
    def convertBTtoArray(self, node):
        
        #Check whether tree is empty
        if(self.root == None):
            print("Tree is empty\n");
            return;
        else:
            if(node.left!= None):
                self.convertBTtoArray(node.left);
            #Adds nodes of binary tree to treeArray
            self.treeArray.append(node.data); 
 
            if(node.right!= None):
                self.convertBTtoArray(node.right);
                
    #createBST() will convert array to binary search tree
    def createBST(self, start, end):
        
        #It will avoid overflow
        if(start > end):
            return None;
            
        #Variable will store middle element of array and make it root of binary search tree
        mid = (start + end) // 2;
        node = Node(self.treeArray[mid]);
        
        #Construct left subtree
        node.left = self.createBST(start, mid - 1);
        
        #Construct right subtree
        node.right = self.createBST(mid + 1, end);
        
        return node;
        
    #inorder() will perform inorder traversal on binary search tree
    def inorderTraversal(self, node):
        
        #Check whether tree is empty
        if(self.root == None):
            print("Tree is empty\n");
            return;
        else:
            if(node.left != None):
                self.inorderTraversal(node.left);
            print(node.data),
            if(node.right!= None):
                self.inorderTraversal(node.right);
                
bt = ConvertBTtoBST();
#Add nodes to the binary tree
bt.root = Node(1);
bt.root.left = Node(2);
bt.root.right = Node(3);
bt.root.left.left = Node(4);
bt.root.left.right = Node(5);
bt.root.right.left = Node(6);
bt.root.right.right = Node(7);
 
#Display given binary tree
print("Inorder representation of binary tree: ");
bt.inorderTraversal(bt.root);
 
#Converts binary tree to corresponding binary search tree
bst = bt.convertBTBST(bt.root);
 
#Display corresponding binary search tree
print("\nInorder representation of resulting binary search tree: ");
bt.inorderTraversal(bst);

Output:

Inorder representation of binary tree: 
4 2 5 1 6 3 7 
Inorder representation of resulting binary search tree: 
1 2 3 4 5 6 7

C

#include <stdio.h>
#include <stdlib.h>
 
//Represent a node of binary tree
struct node{
    int data;
    struct node *left;
    struct node *right;
};
 
//Represent the root of binary tree
struct node *root = NULL;
 
int treeArray[100];
int ind = 0;
    
//createNode() will create a new node
struct node* createNode(int data){
    //Create a new node
    struct node *newNode = (struct node*)malloc(sizeof(struct node));
    //Assign data to newNode, set left and right children to NULL
    newNode->data= data;
    newNode->left = NULL;
    newNode->right = NULL;
    
    return newNode;
}
 
//calculateSize() will calculate size of tree
int calculateSize(struct node *node)
{    
    int size = 0;
    if (node == NULL)
     return 0;
    else {
        size = calculateSize (node->left) + calculateSize (node->right) + 1;
        return size;
    }
}
 
//convertBTtoArray() will convert the given binary tree to its corresponding array representation
void convertBTtoArray(struct node *node) {
    //Check whether tree is empty
    if(root == NULL){
        printf("Tree is empty\n");
        return;
    }
    else {
        if(node->left != NULL)
            convertBTtoArray(node->left);
        //Adds nodes of binary tree to treeArray
        treeArray[ind] = node->data; 
        ind++;
        if(node->right!= NULL)
            convertBTtoArray(node->right);  
        }      
}
 
//createBST() will convert array to binary search tree
struct node* createBST(int start, int end) {
    
    //It will avoid overflow
    if (start > end) {
        return NULL;
    }
    
    //Variable will store middle element of array and make it root of binary search tree
    int mid = (start + end) / 2;
    struct node *temp = createNode(treeArray[mid]);
 
    //Construct left subtree
    temp->left = createBST(start, mid - 1);
 
    //Construct right subtree
    temp->right = createBST(mid + 1, end);
 
    return temp;
}
 
//convertBTBST() will convert a binary tree to binary search tree
struct node* convertBTBST(struct node *node) {
    
    //Variable treeSize will hold size of tree
    int treeSize = calculateSize(node);
    
    //Converts binary tree to array
    convertBTtoArray(node);
    
    //Sort treeArray
    int compare (const void * a, const void * b) {
        return ( *(int*)a - *(int*)b );
    }
    qsort(treeArray, treeSize, sizeof(int), compare);
    
    //Converts array to binary search tree
    struct node *d = createBST(0, treeSize - 1);
    return d;
}
 
//inorder() will perform inorder traversal on binary search tree
void inorderTraversal(struct node *node) {
    
    //Check whether tree is empty
    if(root == NULL){
        printf("Tree is empty\n");
        return;
       }
    else {
        
        if(node->left!= NULL)
            inorderTraversal(node->left);
        printf("%d ", node->data);
        if(node->right!= NULL)
            inorderTraversal(node->right);
    }      
}
      
int main()
{
    //Add nodes to the binary tree
    root = createNode(1);
    root->left = createNode(2);
    root->right = createNode(3);
    root->left->left = createNode(4);
    root->left->right = createNode(5);
    root->right->left = createNode(6);
    root->right->right = createNode(7);
    
    //Display given binary tree
    printf("Inorder representation of binary tree: \n");
    inorderTraversal(root);
    
    //Converts binary tree to corresponding binary search tree
    struct node *bst = convertBTBST(root);
    
    //Display corresponding binary search tree
    printf("\nInorder representation of resulting binary search tree: \n");
    inorderTraversal(bst);
 
    return 0;
}

Output:

Inorder representation of binary tree: 
4 2 5 1 6 3 7 
Inorder representation of resulting binary search tree: 
1 2 3 4 5 6 7

JAVA

import java.util.Arrays;
 
public class ConvertBTtoBST {
    
    //Represent a node of binary tree
    public static class Node{
        int data;
        Node left;
        Node right;
            
        public Node(int data){
            //Assign data to the new node, set left and right children to null
            this.data = data;
            this.left = null;
            this.right = null;
            }
        }
    
    //Represent the root of binary tree
    public Node root;
    
    int[] treeArray;
    int index = 0;
    
    public ConvertBTtoBST(){
        root = null;
    }
    
    //convertBTBST() will convert a binary tree to binary search tree
    public Node convertBTBST(Node node) {
        
        //Variable treeSize will hold size of tree
        int treeSize = calculateSize(node);
        treeArray = new int[treeSize];
        
        //Converts binary tree to array
        convertBTtoArray(node);
        
          //Sort treeArray
        Arrays.sort(treeArray);
      
        //Converts array to binary search tree
        Node d = createBST(0, treeArray.length -1);
        return d;
    }
    
    //calculateSize() will calculate size of tree
    public int calculateSize(Node node)
    {    
        int size = 0;
        if (node == null)
         return 0;
        else {
            size = calculateSize (node.left) + calculateSize (node.right) + 1;
            return size;
        }
    }
    
    //convertBTtoArray() will convert the given binary tree to its corresponding array representation
    public void convertBTtoArray(Node node) {
        //Check whether tree is empty
        if(root == null){
            System.out.println("Tree is empty");
            return;
        }
        else {
            if(node.left != null)
                convertBTtoArray(node.left);
            //Adds nodes of binary tree to treeArray
            treeArray[index] = node.data; 
            index++;
            if(node.right != null)
                convertBTtoArray(node.right);  
            }      
        }
    
    //createBST() will convert array to binary search tree
    public Node createBST(int start, int end) {
        
        //It will avoid overflow
        if (start > end) {
            return null;
        }
        
        //Variable will store middle element of array and make it root of binary search tree
        int mid = (start + end) / 2;
        Node node = new Node(treeArray[mid]);
 
        //Construct left subtree
        node.left = createBST(start, mid - 1);
 
        //Construct right subtree
        node.right = createBST(mid + 1, end);
 
        return node;
    }
    
    //inorder() will perform inorder traversal on binary search tree
    public void inorderTraversal(Node node) {
        
        //Check whether tree is empty
        if(root == null){
            System.out.println("Tree is empty");
            return;
           }
        else {
            
            if(node.left!= null)
                inorderTraversal(node.left);
            System.out.print(node.data + " ");
            if(node.right!= null)
                inorderTraversal(node.right);
              
          }      
      }
    
    public static void main(String[] args) {
        
        ConvertBTtoBST bt = new ConvertBTtoBST();
        //Add nodes to the binary tree
        bt.root = new Node(1);
        bt.root.left = new Node(2);
        bt.root.right = new Node(3);
        bt.root.left.left = new Node(4);
        bt.root.left.right = new Node(5);
        bt.root.right.left = new Node(6);
        bt.root.right.right = new Node(7);
        
        //Display given binary tree
        System.out.println("Inorder representation of binary tree: ");
        bt.inorderTraversal(bt.root);
        
        //Converts binary tree to corresponding binary search tree
        Node bst = bt.convertBTBST(bt.root);
        
        //Display corresponding binary search tree
        System.out.println("\nInorder representation of resulting binary search tree: ");
        bt.inorderTraversal(bst);
      }
}

Output:

Inorder representation of binary tree: 
4 2 5 1 6 3 7 
Inorder representation of resulting binary search tree: 
1 2 3 4 5 6 7

C#

using System;
namespace Tree 
{                     
    public class Program
    {
        //Represent a node of binary tree
        public class Node<T>{
            public T data;
            public Node<T> left;
            public Node<T> right;
            
            public Node(T data) {
                //Assign data to the new node, set left and right children to null
                this.data = data;
                this.left = null;
                this.right = null;
            }
        }
        
        public class ConvertBTtoBST<T>{
            //Represent the root of binary tree
            public Node<T> root;
            
            T[] treeArray;
            int index = 0;
            
            public ConvertBTtoBST(){
                root = null;
            }
        
            //convertBTBST() will convert a binary tree to binary search tree
            public Node<T> convertBTBST(Node<T> node) {
 
                //Variable treeSize will hold size of tree
                int treeSize = calculateSize(node);
                treeArray = new T[treeSize];
 
                //Converts binary tree to array
                convertBTtoArray(node);
 
                //Sort treeArray
                Array.Sort(treeArray);
 
                //Converts array to binary search tree
                Node<T> d = createBST(0, treeArray.Length -1);
                return d;
            }
    
            //calculateSize() will calculate size of tree
            int calculateSize(Node<T> node)
            {    
                int size = 0;
                if (node == null)
                 return 0;
                else {
                    size = calculateSize (node.left) + calculateSize (node.right) + 1;
                    return size;
                }
            }
    
            //convertBTtoArray() will convert the given binary tree to its corresponding array representation
            public void convertBTtoArray(Node<T> node) {
                //Check whether tree is empty
                if(root == null){
                    Console.WriteLine("Tree is empty");
                    return;
                }
                else {
                    if(node.left != null)
                        convertBTtoArray(node.left);
                    //Adds nodes of binary tree to treeArray
                    treeArray[index] = node.data; 
                    index++;
                    if(node.right != null)
                        convertBTtoArray(node.right);  
                    }      
                }
    
                //createBST() will convert array to binary search tree
                public Node<T> createBST(int start, int end) {
 
                    //It will avoid overflow
                    if (start > end) {
                        return null;
                    }
 
                    //Variable will store middle element of array and make it root of binary search tree
                    int mid = (start + end) / 2;
                    Node<T> node = new Node<T>(treeArray[mid]);
 
                    //Construct left subtree
                    node.left = createBST(start, mid - 1);
 
                    //Construct right subtree
                    node.right = createBST(mid + 1, end);
 
                    return node;
                }
    
                //inorder() will perform inorder traversal on binary search tree
                public void inorderTraversal(Node<T> node) {
 
                    //Check whether tree is empty
                    if(root == null){
                        Console.WriteLine("Tree is empty");
                        return;
                       }
                    else {
 
                        if(node.left!= null)
                            inorderTraversal(node.left);
                        Console.Write(node.data + " ");
                        if(node.right!= null)
                            inorderTraversal(node.right);
 
                      }      
                  }
        }
        
        public static void Main()
        {
            ConvertBTtoBST<int> bt = new ConvertBTtoBST<int>();
        
            //Add nodes to the binary tree
            bt.root = new Node<int>(1);
            bt.root.left = new Node<int>(2);
            bt.root.right = new Node<int>(3);
            bt.root.left.left = new Node<int>(4);
            bt.root.left.right = new Node<int>(5);
            bt.root.right.left = new Node<int>(6);
            bt.root.right.right = new Node<int>(7);
 
            //Display given binary tree
            Console.WriteLine("Inorder representation of binary tree: ");
            bt.inorderTraversal(bt.root);
 
            //Converts binary tree to corresponding binary search tree
            Node<int> bst = bt.convertBTBST(bt.root);
 
            //Display corresponding binary search tree
            Console.WriteLine("\nInorder representation of resulting binary search tree: ");
            bt.inorderTraversal(bst);                
        }    
    }
}

Output:

Inorder representation of binary tree: 
4 2 5 1 6 3 7 
Inorder representation of resulting binary search tree: 
1 2 3 4 5 6 7

PHP

<!DOCTYPE html>
<html>
<body>
<?php
//Represent a node of binary tree
class Node{
    public $data;
    public $left;
    public $right;
    
    function __construct($data){
        //Assign data to the new node, set left and right children to NULL
        $this->data = $data;
        $this->left = NULL;
        $this->right = NULL;
    }
}
class ConvertBTtoBST{
    //Represent the root of binary tree
    public $root;
    public $treeArray;
    public $index;
    function __construct(){
        $this->root = NULL;
        $this->treeArray = array();
        $this->index = 0;
    }
    
    //convertBTBST() will convert a binary tree to binary search tree
    function convertBTBST($node) {
        
        //Converts binary tree to array
        $this->convertBTtoArray($node);
        
          //Sort treeArray
        sort($this->treeArray);
      
        //Converts array to binary search tree
        $d = $this->createBST(0, count($this->treeArray) -1);
        return $d;
    }
    
    //convertBTtoArray() will convert the given binary tree to its corresponding array representation
    function convertBTtoArray($node) {
        //Check whether tree is empty
        if($this->root == null){
            print("Tree is empty <br>");
            return;
        }
        else {
            if($node->left != NULL)
                $this->convertBTtoArray($node->left);
            //Adds nodes of binary tree to treeArray
            $this->treeArray[$this->index] = $node->data; 
            $this->index++;
            if($node->right != NULL)
                $this->convertBTtoArray($node->right);  
            }      
        }
    
    //createBST() will convert array to binary search tree
    function createBST($start, $end) {
        
        //It will avoid overflow
        if ($start > $end) {
            return NULL;
        }
        
        //Variable will store middle element of array and make it root of binary search tree
        $mid = ($start + $end) / 2;
        $node = new Node($this->treeArray[$mid]);
 
        //Construct left subtree
        $node->left = $this->createBST($start, $mid - 1);
 
        //Construct right subtree
        $node->right = $this->createBST($mid + 1, $end);
 
        return $node;
    }
    
    //inorder() will perform inorder traversal on binary search tree
    function inorderTraversal($node) {
        
        //Check whether tree is empty
        if($this->root == NULL){
            print("Tree is empty <br>");
            return;
           }
        else {
            
            if($node->left!= NULL)
                $this->inorderTraversal($node->left);
            print("$node->data ");
            if($node->right!= NULL)
                $this->inorderTraversal($node->right);
              
          }      
      }
}
$bt = new ConvertBTtoBST();
//Add nodes to the binary tree
$bt->root = new Node(1);
$bt->root->left = new Node(2);
$bt->root->right = new Node(3);
$bt->root->left->left = new Node(4);
$bt->root->left->right = new Node(5);
$bt->root->right->left = new Node(6);
$bt->root->right->right = new Node(7);
 
//Display given binary tree
print("Inorder representation of binary tree: <br>");
$bt->inorderTraversal($bt->root);
 
//Converts binary tree to corresponding binary search tree
$bst = $bt->convertBTBST($bt->root);
 
//Display corresponding binary search tree
print("<br> Inorder representation of resulting binary search tree: <br>");
$bt->inorderTraversal($bst);      
?>
</body>
</html>

Output:

Inorder representation of binary tree: 
4 2 5 1 6 3 7 
Inorder representation of resulting binary search tree: 
1 2 3 4 5 6 7

Next TopicPrograms List

← prev next →

For Videos Join Our Youtube Channel: Join Now

Feedback

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Splunk

SPSS

Swagger

Transact-SQL

Tumblr

ReactJS

Regex

Reinforcement Learning

R Programming

RxJS

React Native

Python Design Patterns

Python Pillow

Python Turtle

Keras

Preparation

Aptitude

Reasoning

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

AWS

Selenium

Cloud Computing

Hadoop

ReactJS

Data Science

Angular 7

Blockchain

Git

Machine Learning

DevOps

B.Tech / MCA

DBMS

Data Structures

DAA

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

Automata

C Programming

C++

Java

.Net

Python

Programs

Control System

Data Mining

Data Warehouse

^{Like/Subscribe us for latest updates or newsletter}