Program to Find the Total Number of Possible Binary Search Trees with N Keys

Q. Program to find the total number of possible Binary Search Trees with n keys.

Explanation

In this program, we need to find out the total number of binary search trees can be constructed with n values. Below diagram shows a possible binary search tree with the key value as 3. So, we can construct a total of five binary search trees. When we choose node 1 as the root node, we get two trees. Similarly, one tree with 2 as root node and two trees when we select 3 as the root node.

This approach involves selecting a node recursively as the root node and create possible binary search tree.

An easy way to calculate the total number of possible binary search trees are through Catalan number: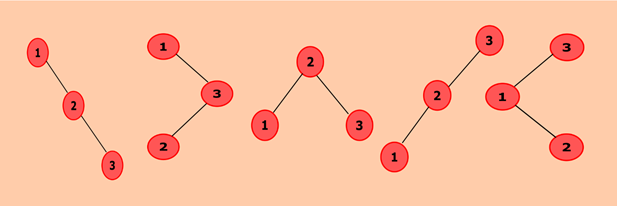

Program to find the total number of possible Binary Search Trees with n keys

Algorithm

Define Node class which has three attributes namely: data left and right. Here, left represents the left child of the node and right represents the right child of the node.
When a node is created, data will be passed to the data attribute of the node and both left and right will be set to null.
Define another class which has an attribute root.
1. Root represents the root node of the tree and initialize it to null.
numOfBST() will find out total possible binary search tree for given key:
1. It will calculate the Catalan number for given key by making a call to factorial().
2. Catalan number can be calculated using the formula:
  Cn = (2n)! / n! *(n+1)!
3. Factorial() will calculate factorial of a given number.

Solution

Python

#Represent a node of binary tree
class Node:
    def __init__(self,data):
        #Assign data to the new node, set left and right children to None
        self.data = data;
        self.left = None;
        self.right = None;
 
class BinarySearchTree:
    def __init__(self):
        #Represent the root of binary tree
        self.root = None;
        
    #factorial() will calculate the factorial of given number
    def factorial(self, num):
        fact = 1;
        if(num == 0):
            return 1;
        else:
            while(num > 1):
                fact = fact * num;
                num = num - 1;
            return fact;
    
    #numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key
    def numOfBST(self, key):
        catalanNumber = self.factorial(2 * key)/(self.factorial(key + 1) * self.factorial(key));
        return int(catalanNumber);
 
bt = BinarySearchTree();
 
#Display the total number of possible binary search tree with key 5
print("Total number of possible Binary Search Trees with given key: " + str(bt.numOfBST(5)));

Output:

Total number of possible Binary Search Trees with given key: 42

C

#include <stdio.h>
#include <stdlib.h>
 
//Represent a node of binary tree
struct node{
    int data;
    struct node *left;
    struct node *right;
};
 
//Represent the root of binary tree
struct node *root = NULL;
 
//createNode() will create a new node
struct node* createNode(int data){
    //Create a new node
    struct node *newNode = (struct node*)malloc(sizeof(struct node));
    //Assign data to newNode, set left and right child to NULL
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}
 
//factorial() will calculate the factorial of given number
int factorial(int num) {
    int fact = 1;
    if(num == 0)
        return 1;
    else {
        while(num > 1) {
            fact = fact * num;
            num--;
        }
        return fact;
    }
}
 
//numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key
int numOfBST(int key) {
    int catalanNumber = factorial(2 * key)/(factorial(key + 1) * factorial(key));
    return catalanNumber;
}
    
int main(){
    
    //Display total number of possible binary search tree with key 5
    printf("Total number of possible Binary Search Trees with given key: %d", numOfBST(5));
    
    return 0;
}

Output:

Total number of possible Binary Search Trees with given key: 42

JAVA

public class BinarySearchTree {
    
    //Represent the node of binary tree
    public static class Node{
        int data;
        Node left;
        Node right;
        
        public Node(int data){
            //Assign data to the new node, set left and right children to null
            this.data = data;
            this.left = null;
            this.right = null;
            }
        }
    
    //Represent the root of binary tree
    public Node root;
    
    public BinarySearchTree(){
        root = null;
    }
    
    //factorial() will calculate the factorial of given number
    public int factorial(int num) {
        int fact = 1;
        if(num == 0)
            return 1;
        else {
            while(num > 1) {
                fact = fact * num;
                num--;
            }
            return fact;
        }
    }
    
    //numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key
    public int numOfBST(int key) {
        int catalanNumber = factorial(2 * key)/(factorial(key + 1) * factorial(key));
        return catalanNumber;
    }
    
    public static void main(String[] args) {
        
        BinarySearchTree bt = new BinarySearchTree();
        
        //Display total number of possible binary search tree with key 5
        System.out.println("Total number of possible Binary Search Trees with given key: " + bt.numOfBST(5));
      }
}

Output:

Total number of possible Binary Search Trees with given key: 42

C#

using System;
namespace Tree 
{                     
    public class Program
    {
        //Represent a node of binary tree
        public class Node<T>{
            public T data;
            public Node<T> left;
            public Node<T> right;
            
            public Node(T data) {
                //Assign data to the new node, set left and right children to null
                this.data = data;
                this.left = null;
                this.right = null;
            }
        }
        
        public class BinarySearchTree<T>{
            //Represent the root of binary tree
            public Node<T> root;
 
            public BinarySearchTree(){
                root = null;
            }
        
            //factorial() will calculate the factorial of given number
            public int factorial(int num) {
                int fact = 1;
                if(num == 0)
                    return 1;
                else {
                    while(num > 1) {
                        fact = fact * num;
                        num--;
                    }
                    return fact;
                }
            }
 
            //numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key
            public int numOfBST(int key) {
                int catalanNumber = factorial(2 * key)/(factorial(key + 1) * factorial(key));
                return catalanNumber;
            }
        }
        
        public static void Main()
        {
            BinarySearchTree<int> bt = new BinarySearchTree<int>();
        
            //Display total number of possible binary search tree with key 5
            Console.WriteLine("Total number of possible Binary Search Trees with given key: " + bt.numOfBST(5));                
        }    
    }

Output:

Total number of possible Binary Search Trees with given key: 42

PHP

<!DOCTYPE html>
<html>
<body>
<?php
//Represent a node of binary tree
class Node{
    public $data;
    public $left;
    public $right;
    
    function __construct($data){
        //Assign data to the new node, set left and right children to NULL
        $this->data = $data;
        $this->left = NULL;
        $this->right = NULL;
    }
}
class BinarySearchTree{
    //Represent the root of binary tree
    public $root;
    function __construct(){
        $this->root = NULL;
    }
    
    //factorial() will calculate the factorial of given number
    function factorial($num) {
        $fact = 1;
        if($num == 0)
            return 1;
        else {
            while($num > 1) {
                $fact = $fact * $num;
                $num--;
            }
            return $fact;
        }
    }
    
    //numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key
    function numOfBST($key) {
        $catalanNumber = $this->factorial(2 * $key)/($this->factorial($key + 1) * $this->factorial($key));
        return $catalanNumber;
    }
}
 
$bt = new BinarySearchTree();
        
//Display total number of possible binary search tree with key 5
print "Total number of possible Binary Search Trees with given key: " . $bt->numOfBST(5);      
?>
</body>
</html>

Output:

Total number of possible Binary Search Trees with given key: 42

Next TopicPrograms List

← prev next →

For Videos Join Our Youtube Channel: Join Now

Feedback

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Splunk

SPSS

Swagger

Transact-SQL

Tumblr

ReactJS

Regex

Reinforcement Learning

R Programming

RxJS

React Native

Python Design Patterns

Python Pillow

Python Turtle

Keras

Preparation

Aptitude

Reasoning

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

AWS

Selenium

Cloud Computing

Hadoop

ReactJS

Data Science

Angular 7

Blockchain

Git

Machine Learning

DevOps

B.Tech / MCA

DBMS

Data Structures

DAA

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

Automata

C Programming

C++

Java

.Net

Python

Programs

Control System

Data Mining

Data Warehouse

^{Like/Subscribe us for latest updates or newsletter}