2D shapesA 2D (or two-dimensional) shape can be defined as a geometrical figure that can be drawn on the coordinate system consist of X and Y planes. It is different from 3D shapes in the sense that every point of the 2D shape always consists of two coordinates (X, Y). 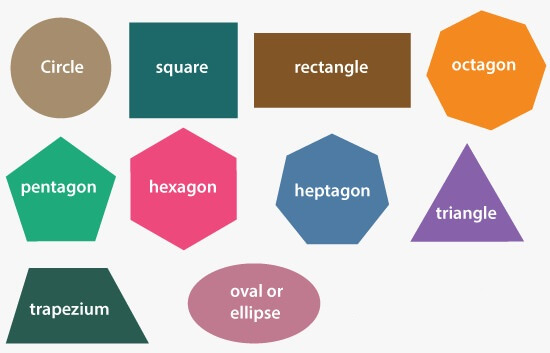
The two-dimensional shapes are the plane figures that can be drawn on a piece of paper or on a flat surface. Some 2D shapes include corners and sides, whereas some have curved boundaries. The 2D shapes with the curved boundaries are the circle and ellipse. Some of the examples of the basic 2D shapes are circle, rectangle, triangle, square, octagon, pentagon, etc. Except for circle, ellipse, and other 2D shapes with curved boundaries, all the shapes are considered to be polygons. A polygon is a representation of the surface. It is primitive which is closed in nature. It is formed using a collection of lines. It is also called a many-sided figure. The lines combined to form polygon are called sides or edges. The lines are obtained by combining two vertices. Let's discuss the basic 2D shapes and their representation using images. We are also discussing their important formulae. CircleA circle is a curved line that has the same distance from the center and connects to the point where it starts. In other words, it is the locus of all points that have equidistant from the origin. The examples of the circle are the wheel, coin, compact disc, etc. It is a round-shaped figure. We can see the representation of the circle in the below image - 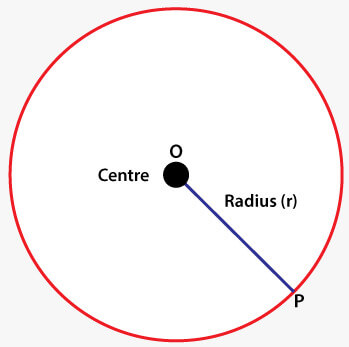
A circle includes various parts such as diameter, radius, circumference, center, tangent, and many more. The types of circles include the tangent circle, concentric circle, and congruent circle. Some of the commonly used formulae of the circle are given as follows - Area of Circle (A) = πr2 Diameter (d) = 2 × radius (r) Radius (r) = Diameter/2 Circumference (C) = 2πr RectangleA rectangle is a two-dimensional shape including four sides, in which the opposite sides are parallel and equal. Rectangle is the geometrical figure with two pairs of two equal sides and four right angles at their joint. A rectangle is a polygon that has four sides. The property of a rectangle is that the length of the opposite sides must be equal. We can find the area of a rectangle by using the formula that includes length and breadth. The examples of the rectangle are brick, cardboard, etc. We can see the representation of the rectangle in the below image - 
The formula for finding the area of a rectangle is equal to the product of the length and breadth of the rectangle. Area of Rectangle (A) = Length × Breadth SquareA square is a closed figure on a 2D plane that has four parallel and equal sides. The property of the square is that all the sides (breadth and length) must have equal length. In a square, each angle is 90°. The representation of the square is shown in the below image - 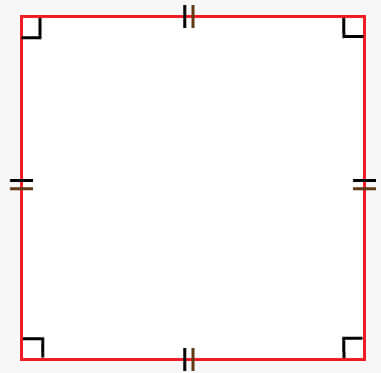
The formula for finding the area of square is given as follows - Area of square (A) = a × a Or, Area of square (A) = (a) 2 Where a is the side of the square whose length is a. TriangleA triangle is a polygon that has three vertices and three edges. The sum of three interior angles of a triangle is 180 degrees. Triangle has various types such as equilateral triangle, isosceles triangle, scalene triangle, acute triangle, etc. Every type has its own properties, but the common thing is all are having three sides, and sum of their interior angles is equal to 180 degrees. The best example of the triangle is a pyramid. The representation of a triangle is shown in the below image: 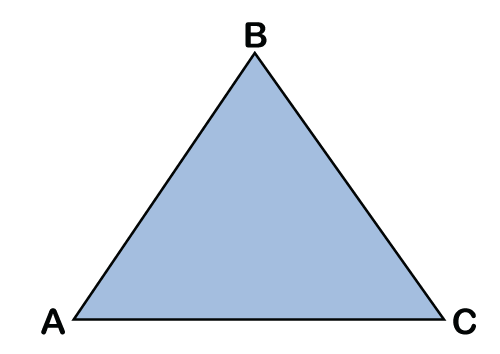
The formula to calculate the area can be different for different types of triangles. The area of a triangle is the region covered by a triangle. The area of a triangle is equal to half of the base multiplied by the perpendicular height of the triangle. If the given triangle is a right triangle, multiply the two sides together, which are adjacent to the right angle. Here, we are discussing two formulae to calculate the area of triangle. The formulas for calculating the triangle's area are given as follows - 1. It is the half of the base multiplied by the height. The formula given below works for all triangles. Area of Triangle (A) = ½ × b × h Where b denoted the base and h denote the height of the given triangle. 2. Heron's formula can also be used to find the area of a triangle. But it can be applied when all sides of the triangle are given or if all three sides are unequal. Area of a Triangle (A) = √(s(s-a)(s-b)(s-c)) Where a, b, c are the sides of triangle and s is the semi-perimeter, which can be calculated as - semi-perimeter (s) = (a + b + c) / 2 There can be other formulae to calculate the area of triangle based on different properties. ParallelogramA parallelogram can be defined as a quadrilateral (four sides) shape having two pairs of parallel lines. The opposite sides and congruent angles are equal in measure. The sum of the interior angles of a parallelogram is 360°. The special types of parallelogram include Rhombus, Square, Rectangle, and Rhomboid. The representation of a parallelogram is shown in the below image - 
The opposite sides and angles of a parallelogram are congruent. The formula for finding the area of a parallelogram is same as the rectangle. This is because a parallelogram can be converted into a rectangular shape. To find the area of parallelogram, multiply the base by its height and vice versa. In other words, the area of a parallelogram is base times height. Area of parallelogram (A) = base (b) * height (h) TrapeziumThe trapezium is a convex quadrilateral shape. It means that a closed-shape with four sides along with one pair of parallel sides. The trapezium (also called as trapezoid) is a geometrical shape including four-sides in which a pair of opposite sides is parallel. The parallel sides are known as base, and the non-parallel sides are known as leg. The parallel sides can be horizontal, vertical, or slanting (diagonal). The representation of the trapezium is shown in the below image - 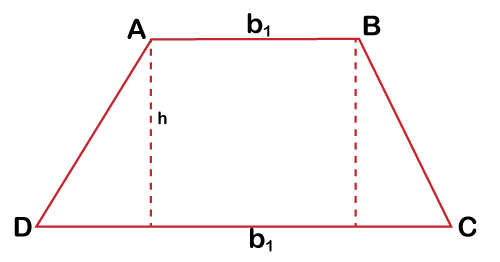
The formulae for finding the area and perimeter of the trapezium are given as follows - Area of trapezium (A) = ½ (b1 + b2) * h Or, Area of trapezium (A) = h/2 * (b1 + b2) Or, Area of trapezium (A) = h * (b1 + b2/2) Perimeter of trapezium = Sum of all sides = AB + BC + CD + DA
Next TopicConstant variable definition
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









