Power Formula

Power is defined as the amount of work done per unit time. Power is required everywhere to perform a task, be it physically or mechanically. The concept remains the same, i.e., the ability required to complete a task at a specific time.

Characteristics of power

The characteristics of power are as follows:

• One Watt is defined as 1 joule of energy per second.
• It is a scalar quantity.
• Power is often defined as an activity.
• Power is the time derivative of the work done. It can be expressed as P = dW/dt.
• Power is also measured in terms of horsepower, which is equal to 745.7 watts.
• Other power units are kilowatt, milliwatt, ergs per second, dBm (decibels- milliwatt), and calories per hour.
• The amount of work done per time can be different for different substances. For example, TNT (Trinitrotoluene) delivers more power as compared to coal. It is because the reaction of TNT releases energy more quickly than coal.
• In a mechanical system, the input power can be equal to the output power if there are no such losses in the system.

We can define the power formula as mechanical power, gravitational power, electric power, and power in terms of force, displacement, and velocity. It is given below: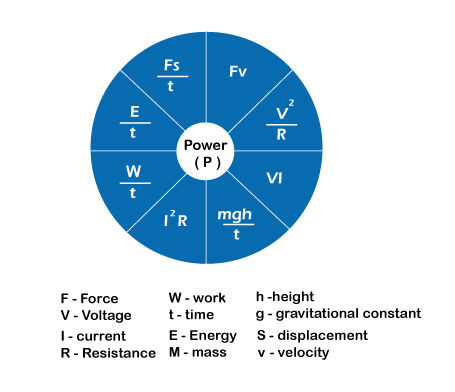

Let's discuss the various power formulas.

Mechanical power

It is defined as the energy of a system per unit time.

P = E/t

Where,

P is the power

E is the energy

T is the time

The watt, joules, and second are the unit of power, energy, and time.

Power is also expressed as:

P = w /t

Where,

W is the work done, t is the time, and P is the power.

Gravitational power

It is measured with respect to g, which is the gravitational constant with the value of 9.8 meters per Second Square. The gravitational power is expressed as:

P = mgh / t

Where,

P is the power

m is the mass

h is the height

t is the time

Mass is generally measured in Kilograms, and height in meters.

Electrical power

The electrical power is expressed as:

P = V I

Where,

P is the power

V is the voltage

I is the current

Electric power is defined as the product of the current and the potential across the circuit.

According to Ohm's law, I = V/R

Where,

I is the current

R is the resistance measured in Ohms

V is the voltage

Substituting the value of I in the given power formula, we get:

P = V x I

P = V x (V/R)

P = V^2/R

Or

P = V x I

P = (IR) x I

P = I^2R

Power in terms of force, displacement, and velocity

It is expressed as:

Power = Force x Displacement/ Time

P = Fs/t

Where,

F is the force measured in Newton

S is the displacement measured in meter

T is the time

We can also write the above equation as:

P = Force x velocity

P = Fv

(As velocity = displacement/time)

Let's discuss numerical examples and MCQs on power for better understanding.

Numerical examples

Consider the following examples.

Example 1: An electric machine uses the energy of 200J in 10 seconds. Find the power used by the machine?

Solution: The given parameters are:

E = 200J

T = 10s

The power is given by:

P = E/t

P = 200/10 = 20W

Thus, the power required by the machine is 20 Watts.

Example 2: Henry has of mass of 50 kg and runs upto 10m high in 20 seconds. Find the power.

Solution: The given parameters are as follows:

Mass = 50 kg

Height = 10m

Time = 20 seconds

The gravitational power can be computed as P = mgh/t

Where, g = 9.8 meter per second square

P = 50 x 9.8 x 10 / 20

P = 245 Watts

Thus, the power is 245 watts.

Example 3: The voltage and current of the electrical circuit are given as 15V and 2A. Find the electric power of the circuit.

Solution: The given parameters are as follows:

Voltage = 15 Volts

Current = 2 Ampere

P = V x I

P = 15 x 2 = 30 Watts

Thus, the power of the electrical circuit is 30 watts.

Example 4: A constant force of 10N is applied on an object moving at a constant velocity of 4 m/s. Compute the power.

Solution: The given parameters are as follows:

Force = 10N

Velocity = 4m/s

Power can be computed as, P = Force x velocity

P = 10 x 4 = 40 Watts

Thus, the power is 40 watts.

Example 5: Find the power of the electrical circuit with a resistance of 2 Ohms and the current of 3A.

Solution: The given parameters are as follows:

Resistance = 2 Ohms

Current = 3 Ampere

P = I^2R

P = 3 x 3 x 2

P = 18 Watts

Thus, the power is 8 watts.

Multiple Choice Questions on power

The MCQs based on power formula are as follows:

1) Which one of the following is a correct power formula?

1. Power = work done x time
2. Power= energy / time
3. Power = force x time
4. Power = velocity / time

2) S.I. unit of power is:

1. Joules
2. Newton
3. Amperes
4. Watt

3) The name of the device used to measure power is:

1. Voltmeter
2. Ammeter
3. Wattmeter
4. None of the above

4) Kilowatt-hour is a unit of?

1. Velocity
2. Force
3. Energy
4. Power

5) Power is directly proportional to:

1. Voltage
2. Current
3. Both (a) and (b)
4. None of these