Types of AnglesThere are many types of shapes used for study purposes in geometry, and an angle is one of them. There are several types of angles in geometry that help structure more complex geometrical shapes and figures. These structures eventually help to study geometrical fundamentals. Angles also play a crucial role in our real-life activities, such as architects and engineers, use different angles while designing buildings, bridges, roads, machinery, etc. There are many more applications of angles in our daily life. Therefore, it is essential to know different angles and take advantage of them in our day-to-day activities. Before we discuss the various angle types, let us first understand the fundamentals and characteristics of angles: What is an Angle?When two or more rays or lines intersect at a point, an angle (or angles) is formed at their intersection. It is usually an amount of turn at a common point. The two rays can follow various fashions to intersect each other and form different angles. Angles are measured in degrees (°). 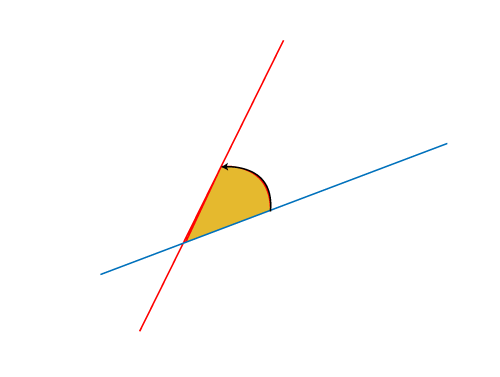
Note: The name 'Angle' originated from the Latin word 'Angulus'.Parts of an AngleThere are three essential parts required to form an angle, such as:

Types of AnglesThere are various types of angles based on different measurements. However, all such angles are typically categorized based on the following two measurements:
Let us discuss each type in detail: Classification of Angles based on MagnitudeBased on the degree measurement and magnitude, angles are usually divided into the following types:
What is a Zero Angle?A zero angle refers to an angle formed when both the angle's arms are in the same direction and the same position. Typically, no angle is formed in this position. Therefore, it is known as a zero angle and measured by zero degrees (0°). The following diagram represents that both arms, PR, and PQ, are in the same position. 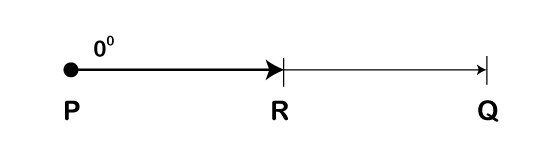
The angle formed here is a zero angle, i.e.: ∠ RPQ = 0° (zero angle) What is an Acute Angle?An acute angle is defined as an angle that lies between 0° to 90°. More specifically, each angle that is more than 0° and less than 90° is an example of an acute angle. For examples, 15°, 30°, 45°, 60°, etc. The following diagrams illustrate acute angles, where an angle in each diagram is greater than 0° but less than 90°. 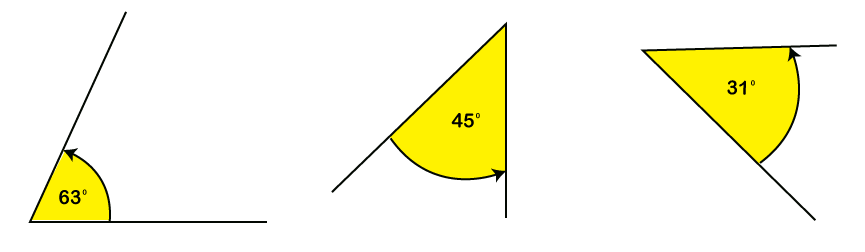
What is a Right Angle?The right angle refers to an angle that is equal to 90 degrees. The angle can neither less than or more than 90 degrees. A right angle is typically formed when the two arms (or lines) of the angle intersect perpendicularly. The angle formed here is usually represented by creating a square-shaped box between the arms of an angle near the vertex. The following diagrams are some examples of the right angles, where an angle in each diagram is precisely equal to 90°. 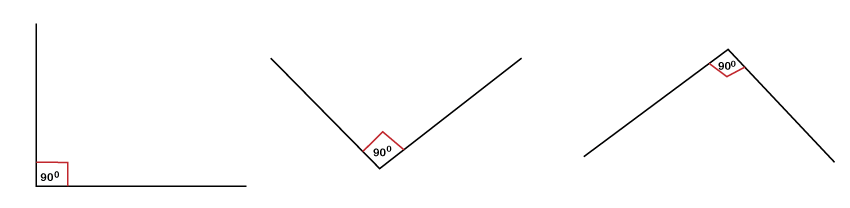
What is an Obtuse Angle?An obtuse angle is just the opposite of an acute angle. An obtuse angle is usually defined as an angle that lies between 90° to 180°. In other words, every angle that is greater than 90° and less than 180° is an example of an obtuse angle. For examples, 100°, 120°, 145°, 160°, etc. The following diagrams are some examples of the obtuse angles, where an angle in each diagram is greater than 90° but less than 180°. 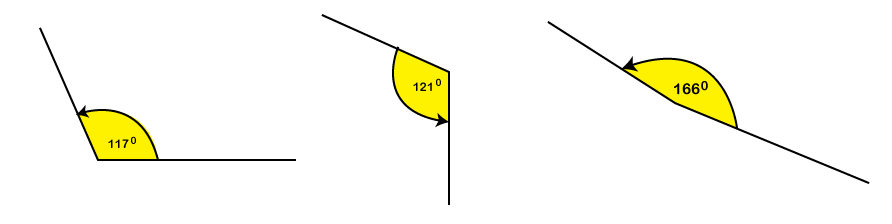
What is a Straight Angle?A straight angle is a mixture of an acute angle and an obtuse angle in a line. In simple terms, when two arms of an angle are in the opposite direction and making a straight line, the angle formed between arms is called a straight angle. The name straight angle is used because of a straight line. The straight angle is exactly equal to 180 degrees. It is essential to that that this can neither be less than or more than 180 degrees. The following diagram represents that both arms, PR, and PQ, are in the opposite direction. 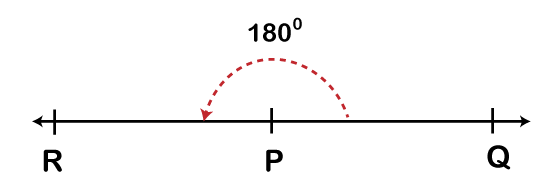
The angle formed here is the straight angle, i.e.: ∠ RPQ = 180° (straight angle) What is a Reflex Angle?A reflex angle is an angle formed between a straight angle (180 degrees) and a whole turn of the terminal arm (side). In simple terms, a reflex angle refers to an angle that lies between 180° to 360°. In other words, every angle that is greater than 180° and less than 360° is an example of a reflex angle. For examples, 200°, 220°, 245°, 260°, 320°, etc. The following diagrams are some examples of the reflex angles, where an angle in each diagram is greater than 180° but less than 360°. 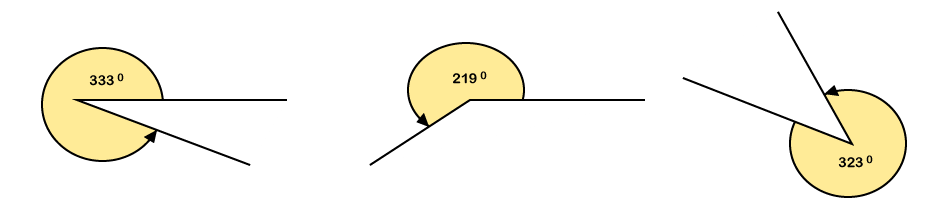
What is a Complete Angle?The complete angle is an angle that is equal to 360°. The angle can neither less than or more than 360 degrees. The complete angle is typically formed when one of the two arms turns completely, taking a complete rotation from a base position to form an angle. In other words, an angle of one revolution or one whole turn is equal to 360 degrees. It is also known as full rotation angle and full angle. The following diagram represents an angle's arm making a whole turn; thus, the name is the complete angle. 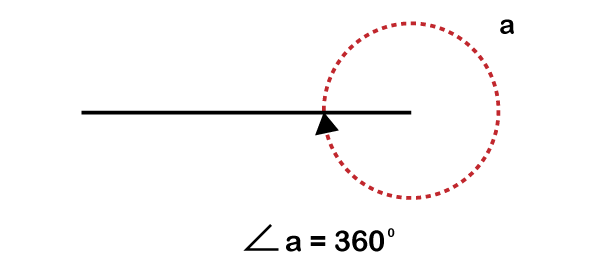
The angle formed here is the complete angle, i.e.: ∠ a = 360° (complete angle) Classification of Angles based on RotationBased on the direction-measurement or the direction of rotation, angles are mainly divided as below:
Positive angles are defined as angles measured in a counterclockwise direction (direction opposite to the clockwise) from the base position (origin). Most of the time, positive angles are used in geometry to represent angles for study purposes. These angles are drawn in the (+x, +y) plane from the origin. The following are some examples of the positive angles where an angle goes counterclockwise from the base position: 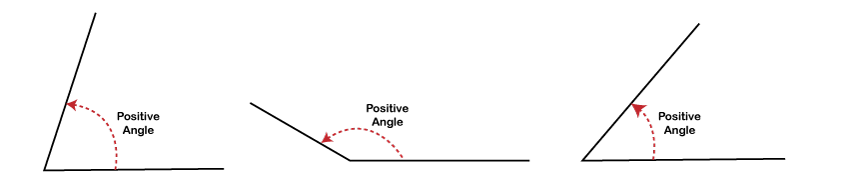
What are Negative Angles?Negative angles are just opposite to the positive angles. This means that the angles measured in a clockwise direction from the base are the negative angles. These angles are drawn in the (+x, -y) plane from the base position. The following are some examples of the negative angles where an angle goes clockwise from the base position: 
Other Types of AnglesApart from the angles mentioned above, there are some other types of angles. Such angles are formed by joining the two angles, making a whole new form of an angle. Because these angles appear in pairs, they are also termed as the 'Pair Angles'. The following are the types of all such angles, which are formed by pair of angles:
Adjacent anglesWhen two angles are connected in such a way that they have a common vertex and one common arm, they are termed adjacent angles. Moreover, the non-common arm of both connected angles lies opposite sides of the common arm. The following diagrams are some examples of the adjacent angles, where there is a common vertex, one common arm, and a non-common arm lying on either side of the common arm. 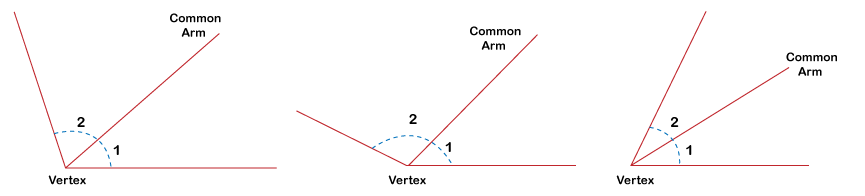
Complementary anglesWhen measuring the sum of two angles adds up to 90°, they are termed complementary angles. It is not compulsory to be only the adjacent angles to be called complementary angles. As long as two angles add up to 90 degrees, they are complementary angles. The following diagrams are examples of the complementary angles where each diagram's two angles add up to measure 90°. 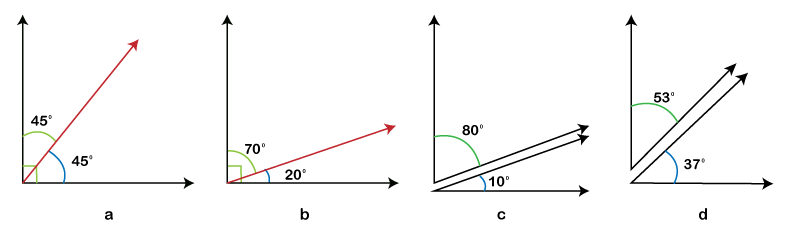
It can be seen here that the diagram 'a' and the diagram 'b' are adjacent angles, but their angles add up to 90 degrees, and so they are also called the complementary angles. Besides, the diagrams 'c' and 'd' are not adjacent; however, their angles also add up to 90 degrees, and so they are called the complementary angles. Supplementary anglesSupplementary angles are similar to complementary angles. However, there is one big difference. The two angles always add up to measure 180 degrees in supplementary angles, instead of 90 degrees like the complementary angles. The following diagrams illustrate the supplementary angles where the two angles in each diagram add up to measure 180°. 
Supplementary angles are further sub-divided into the following types: Vertical AnglesVertical angles refer to all such angles formed using a common vertex and the same sides (arms). Vertical angles are measured exactly equal to each other. They are sometimes termed vertically opposite angles. The following diagram represents vertical angles: 
Here, angles 1 and 2 are the vertical angles. Similarly, angles 3 and 4 are also vertical angles. Interior and Exterior AnglesConsider a diagram where two parallel lines are crossed by a third line (called Transversal). It will look like the diagram given below: 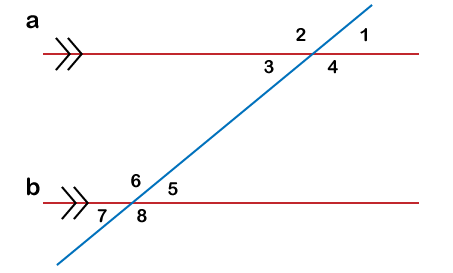
Here, it is clear that there are a total of 8 angles in this diagram. The angles 1 & 3, 2 & 4, 6 & 8, 5 & 7 are vertical angles as they have common vertex and same arms. Besides, the angles that are formed in the internal parts are called interior angles. In the above diagram, angles denoted by 3, 4, 5, 6 are the interior angles. In the same way, the angles that are formed in the external parts are called the exterior angles. Here, angles 1, 2, 7, 8 are examples of exterior angles. Let us now understand a few more angles considering the same diagram: Alternate Interior AnglesAlternate interior angles refer to the pair of interior angles formed opposite the third line (Transversal). The simplest method to find alternate interior angles is to consider 'Z' on the interior sides. In the above diagram, angles 3 & 5 and angles 4 & 6 are examples of alternate interior angles. These angles remain exactly equal to each other (i.e., ∠ 3 = ∠ 5 and ∠ 4 = ∠ 6). Alternate Exterior AnglesAlternate exterior angles follow the same rules as interior angles but on the external parts. In simple terms, the alternate exterior angles refer to the pair of exterior angles formed opposite the third line (Transversal). In the above diagram, angles 1 & 7 and angles 2 & 8 are examples of alternate exterior angles. Like alternate interior angles, alternate exterior angles are also equal (such as ∠ 1 = ∠ 7 and ∠ 2 = ∠ 8). Corresponding AnglesCorresponding angles refer to the pair of all such angles which are present in a similar position. Corresponding angles are also equal. In the above diagram, angles 1 & 5, angles 2 & 6, angles 4 & 8, angles 3 & 7 are the corresponding angles. Also, they are equal, such as ∠ 1 = ∠ 5, ∠ 2 = ∠ 6, etc. Linear PairWhen non-common arms of an adjacent angle are exactly opposite, they form a linear pair angle. It is essential to note that both non-common arms together make a straight line. The following diagrams illustrate the linear pair angles. Here, in each diagram, the non-common arms form a straight line. 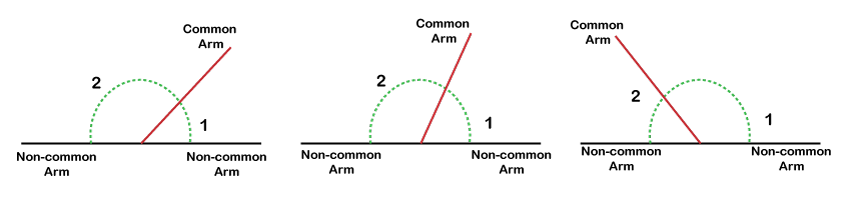
Next TopicTypes of Cell
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









