Greek Euclid's Algorithm

Euclid's algorithm is a mathematical algorithm. This algorithm is typically used to find the GCD of two positive integers. This algorithm is named after the Greek mathematician Euclid.

What is a GCD?

The term GCD stands for the Greatest-Common-Divisor. The GCD is the greatest number that is a common denominator of given numbers. It is also known as the GCF or HCF. Where, GCF stands for the Greatest Common Factor, and HCF stands for the Highest Common Factor.

How to find two positive numbers GCD?

These are three important conditions for finding the GCD:

1. If x = 0, then GCD(x, y) = y because GCD (0, y) = y.
2. If y = 0, then GCD(x, y) = x because GCD (x, 0) = x.
3. If x = y ? 0, then GCD(x, y) = (x = y * Q + R)      
Where, x is a dividend.
             y is a divisor.
             Q is a quotient. 
             R is a remainder.

Let's take examples to understand these conditions.

Example 1: Find the GCD of the A = 0, and B = 1023.

Given, 
             x = 0
             y = 1023

x is 0, so GCD(0, 1023) = 1023

Example 2: Find the GCD of the A = 120, and B = 0.

Given, 
             x = 120
             y = 0

y is 0, so GCD(120, 0) = 120

Example 3: Find the GCD of the A = 30, and B = 18.

Given,
             x = 30
             y = 18
             30 / 18 = 1 with remainder 12
             30 = 18 * 1 + 12
             GCD(30, 18) = GCD(18, 12)

Now, 
             x = 18
             y = 12
             18 / 12 = 1 with remainder 6
             18 = 12 * 1 + 6
             GCD(18, 12) = GCD(12, 6)
Now, 
             x = 12
             y = 6
             12 / 6 = 2 with remainder 0
             12 = 6 * 2 + 0
             GCD(12, 6) = GCD(6, 0)
Now,    
             x = 6
             y = 0
y is a zero, so GCD(6, 0) = 6

GCD(30, 18) = GCD(18, 12) = GCD(12, 6) = GCD(6, 0) = 6
GCD(30, 18) = 6

Example 4: Find the GCD of the A = 270, and B = 192.

Given, 
             x = 270
             y = 192
             270 / 192 = 1 with remainder 78
             270 = 192 * 1 + 78
             GCD(270, 192) = GCD(192, 78)
Now,
             x = 192
             y = 78
             192 / 78 = 2 with remainder 36
             192 = 78 * 2 + 36
             GCD(192, 78) = GCD(78, 36)
Now, 
              x = 78
              y = 36
              78 / 36 = 2 with remainder 6
              78 = 36 * 2 + 6
              GCD(78, 36) = GCD(36, 6)
Now, 
               x = 36
               y = 6
               36 / 6 = 6 with remainder 0
               36 = 6 * 6 + 0
               GCD(36, 6) = GCD(6, 0)
Now, 
               x = 6
               y = 0        
y is a zero, so GCD(6, 0) = 6

GCD(270, 192) = GCD(192, 78) = GCD(78, 36) = GCD(36, 6) = GCD(6, 0) = 6
GCD(270, 192) = 6

Algorithm of GCD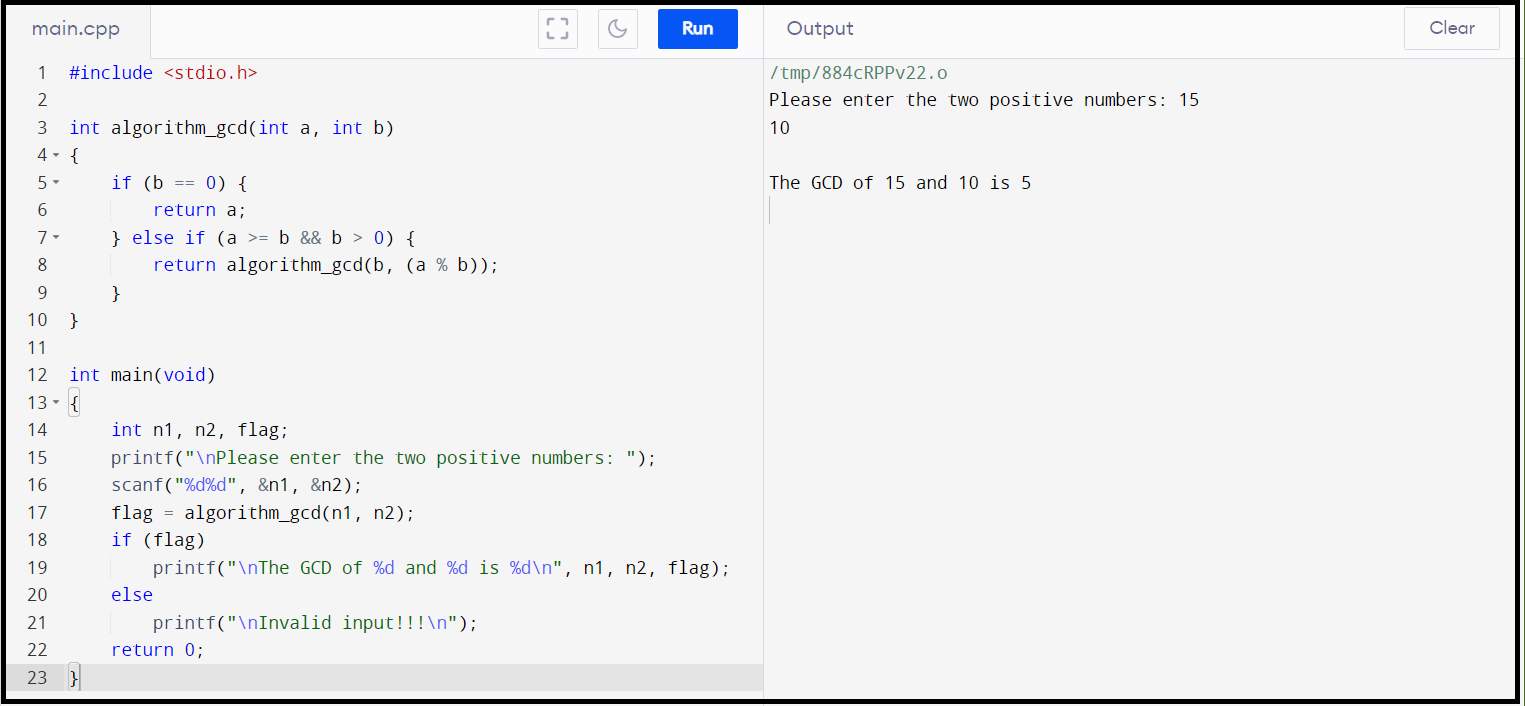

GCD (x, y)
Step 1: if y = 0, return the value of x as the answer and exit, otherwise proceed to step 2.
Step 2: Divide x by y and assign the value of the remainder to r (i.e. r = x mod y).
Step 3: Replace x with y and y with r (i.e. x = y and y = r ? GCD(y, r)), and go to step 1. 

Program

#include <stdio.h>
 
int algorithm_gcd(int a, int b)
{
    if (b == 0) {
        return a;
    } else if (a >= b && b > 0) {
        return algorithm_gcd(b, (a % b));
    }
}
 
int main(void)
{
    int n1, n2, flag;
    printf("\nPlease enter the two positive numbers: ");
    scanf("%d%d", &n1, &n2);
    flag = algorithm_gcd(n1, n2); 
    if (flag)
        printf("\nThe GCD of %d and %d is %d\n", n1, n2, flag);
    else
        printf("\nInvalid input!!!\n");
    return 0;
}

Output:

/tmp/884cRPPv22.o
Please enter the two positive numbers: 15
10

The GCD of 15 and 10 is 5

Next TopicAngular Material (MAT) Form-Field

← prev next →

For Videos Join Our Youtube Channel: Join Now

Feedback

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Splunk

SPSS

Swagger

Transact-SQL

Tumblr

ReactJS

Regex

Reinforcement Learning

R Programming

RxJS

React Native

Python Design Patterns

Python Pillow

Python Turtle

Keras

Preparation

Aptitude

Reasoning

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

AWS

Selenium

Cloud Computing

Hadoop

ReactJS

Data Science

Angular 7

Blockchain

Git

Machine Learning

DevOps

B.Tech / MCA

DBMS

Data Structures

DAA

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

Automata

C Programming

C++

Java

.Net

Python

Programs

Control System

Data Mining

Data Warehouse

^{Like/Subscribe us for latest updates or newsletter}

Blog