Heron's formulaHeron's formula is also known as Hero's formula. It was named after the Greco-Egyptian engineer and mathematician named Hero of Alexandria. It is used to calculate the triangle area when the three sides of a triangle are known. Heron's formula is given by: 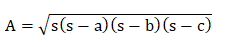
OR 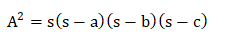
Where, S =Semi-perimeter of the triangle It is given by s = (a + b + c) /2 Semi - perimeter: It is called semi-perimeter because its value is one-half the perimeter of the triangle. Perimeter is defined as the sum of all sides of a given figure. In the case of a triangle, perimeter is equal to the sum of its three sides. The variables a, b, and c are the sides of the triangle. Heron's formula is different from other formulas because it does not require any angle measurements. We can also write the formula in the terms of the sides of the triangle. We need to use s = (a + b + c) /2 in the formula. It is given by: 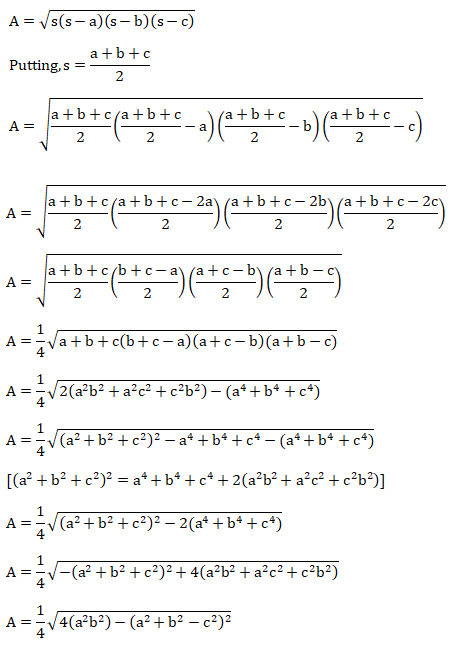
The above formula is also the Heron's formula, but without the semi-perimeter (s). It is specified in the terms of the three sides of the triangle (a, b, and c). Practical problemsLet's solve some practical problems related to Heron's formula. Example 1: Find the area of the triangle with sides a = 4m, b = 5m, and c = 3m. Solution: The triangle semi-perimeter = s = (a + b + c)/2 S = 4 + 5 + 3/2 = 12/2 = 6m The area of triangle A = (6 (6 - 4) (6 - 5) (6 - 3))^1/2 A = (6 x 2 x 1 x 3)^1/2 A = (36)^1/2 A = 6m^2 Hence, the area of triangle is 6 meters square. Example 2: Find the area of the triangle, if the two sides of the triangle are 4m and 3m. The semi-perimeter of the triangle is 5m. Solution: Here, we will first find the third side of the triangle using the semi-perimeter formula. After that, we will find the area of the triangle. We know, S = (a + b + c)/2 5 = (4 + 3 + c)/2 5 x 2 = 4 + 3 + c 10 = 7 + c 3 = c Hence, the third side of the triangle is 3 cm. Area of triangle is given by: 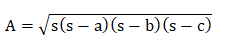
A = [5 (5 - 4) (5 - 3) (5 - 3) ]^1/2 A = [5 x 1 x 2 x 2] ^1/2 A = (20)^1/2 A = 4.47 meter square Thus, the area of triangle is 4.47 meters square. Example 3: Find the area of an equilateral triangle with side of 4m. Solution: The three sides of an equilateral triangle are equal. It means, a = b = c = 4m We can write its semi-perimeter as: S = a + b + c / 2 S = 4 + 4 + 4 /2 S = 12/2 = 6m The area can be expressed as: A = (6 (6 - 4) (6 - 4) (6 - 4))^1/2 A = (6 x 2 x 2 x 2)^1/2 A = 4 (3)^1/2 A = 6.93 m^2 Hence, the area of triangle is 6.93 meters square. Hero of AlexandriaHeron's formula was named after the Hero of Alexandria. He was born around 10AD and died around 70AD. He was the representative of the Roman scientific tradition. His works include Metrica, Mechanica, Automata, etc. Let's discuss a short description of his famous works.
Trigonometric proof of Heron's formulaLet's discuss three trigonometric methods that act as proof for the Heron's formula.
Law of cosinesLet's discuss the first proof using the law of cosines. It means that we use the law of cosines formula to derive the Heron's formula. Heron's has provided the proof of formula in his book Metrica. The trigonometric proof is quite different from that proof discussed in the geometrical formulas book Metrica. According to the law of cosines, 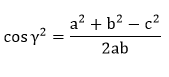
Where, a, b, and c are the sides of the triangle. Alpha, beta, and Gamma are the angles opposite to the sides of the triangle. The triangle with three sides and angles is shown in the below image: 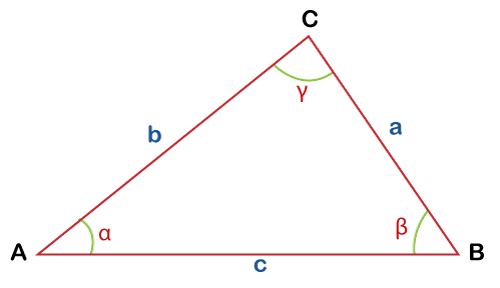
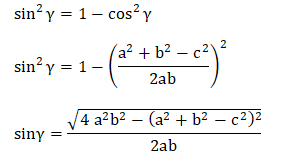
The area of the triangle is given by: ½ x base x altitude Where, siny is the altitude of the triangle. Hence, we can represent the area of the triangle as: 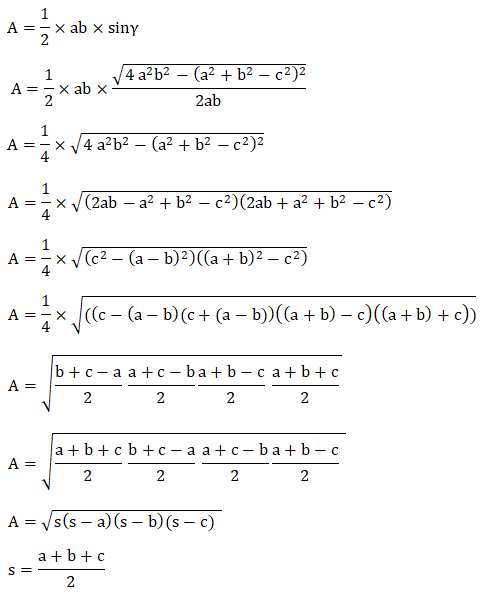
Hence, Heron's formula is proved using the law of cosines. Law of cotangents proofIt is also called as Cot Theorem. It includes the circle inscribed in the triangle, as shown below: 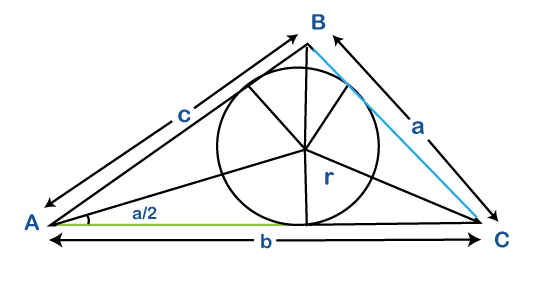
Where, a, b, and c are the sides of the triangle. Alpha, beta, and Gamma are the angles opposite to the sides of the triangle. 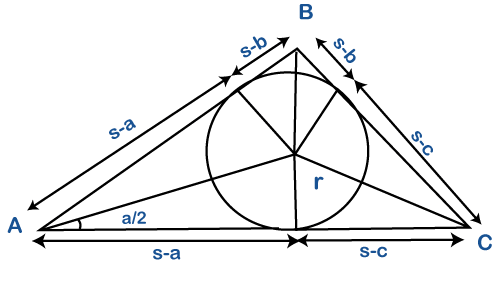
S is the semi-perimeter, which is given by: S = (a + b + c)/2 The area can be computed as: 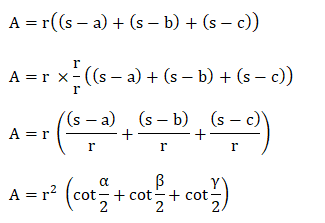
From the above figure, we can easily compute the value of the angle. Cot = base of the triangle/ perpendicular Cot alpha = s - a/r Similarly, other angles can be computed. We know that the sum of half angles is 90 degrees. Thus, we can also compute the area as: A = rs 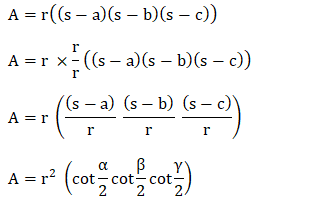
Combining the two different equations of area, we get: 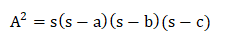
It is the required heron's formula. Law of Pythagorean TheoremA right triangle is shown below: 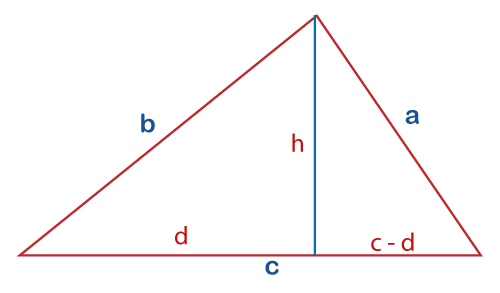
Pythagorean Theorem applies to the right angle triangle, where the square of hypotenuse is equal to the sum of the other two sides of triangle (base and perpendicular). The hypotenuse is considered as the longest side of the triangle. According to the theorem, (Hypotenuse)^2 = (base)^2 + (perpendicular)^2 The above figure comprises two right angle triangles. One triangle is represented by sides' b, d, and h. Another triangle is represented by three sides a, h, and (c - d). The Pythagorean equation for both the triangles can be written as: 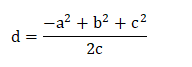
The height of the triangle using the Pythagorean equation is: (Perpendicular)^2 = (Hypotenuse)^2 - (base)^2 Substituting the value of d and h in the Pythagorean equation, we get: 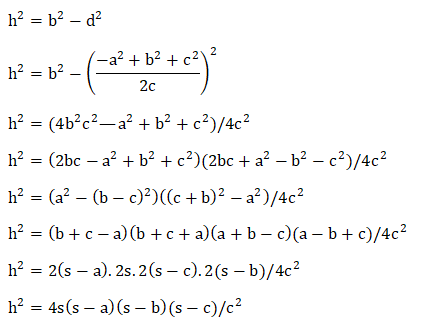
We know that the area of the triangle is given by: A = ½ x base x height A = ½ ch Thus, we can compute the value of the area as: 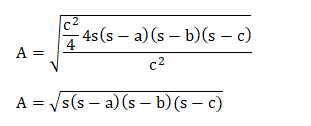
It is the heron's formula, thus proved.
Next TopicGeneral Science MCQ
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









