What is t-Test?

A t-test is a type of inferential statistic used to determine the significant difference between the means of two groups, which may be related to certain features. A t-test is used as a hypothesis testing tool, which allows testing an assumption applicable to a population.

A t-test looks at the t-statistic, the t-distribution values, and the degrees of freedom to determine the statistical significance. A t-test allows us to compare the two data sets' average values and determine if they came from the same population.

For example, if we take a sample of students from class A and another sample of students from class B, we don't get the same mean and standard deviation. Similarly, samples taken from the placebo-fed control group and those taken from the drug prescribed group should have a slightly different mean and standard deviation.

Mathematically, the t-test takes a sample from each of the two sets and establishes the problem statement by assuming a null hypothesis that the two means are equal. Based on the applicable formulas, certain values are calculated and compared against the standard values, and the assumed null hypothesis is accepted or rejected.

If the null hypothesis qualifies for rejection, it indicates that data readings are strong and not due to chance. The t-test is just one of many tests used for this purpose. Statisticians must additionally use tests other than the t-test to examine more variables and tests with larger sample sizes. Statisticians use a z-test for a large sample size. Other testing options include the chi-square test and the f-test.

T-Test Assumptions

1. The first assumption regarding t-tests concerns the scale of measurement. A t-test assumes that the measurement scale applied to the data collected follows a continuous or ordinal scale, such as the IQ test scores.
2. The second assumption is that of a simple random sample that the data is collected from a representative, randomly selected portion of the total population.
3. The third assumption is the data, when plotted, results in a normal distribution, bell-shaped distribution curve.
4. The final assumption is the homogeneity of variance. Homogeneous or equal variance exists when the standard deviations of samples are approximately equal.

When to Use a T-Test?

A t-test is only used when comparing the means of two groups' also known as a pairwise comparison. If you want to compare more than two groups or make multiple pairwise comparisons, use an ANOVA test or a post-hoc test.

The t-test is a parametric test of difference, which means it makes the same assumptions about your data as other parametric tests.

1. The t-test assumes your data are independent.
2. The t-test assumes your data are (approximately) normally distributed.
3. The t-test assumes your data have a similar amount of variance within each group than the homogeneity of variance.

If your data do not fit these assumptions, you can try a non-parametric alternative of the t-test, such as the Wilcoxon Signed-Rank test for data with unequal variances.

Types of T-Tests

There are three types of t-tests we can perform based on the data, such as:

1. One-Sample t-test

In a one-sample t-test, we compare the average of one group against the set average. This set average can be any theoretical value, or it can be the population mean.

In a nutshell, here's the formula to calculate or perform a one-sample t-test:

Where,

• t = t-statistic
• m = mean of the group
• µ = theoretical value or population mean
• s = standard deviation of the group
• n = group size or sample size

Note: As mentioned earlier in the assumptions, a large sample size should be taken for the data to approach a normal distribution. Although t-test is essential for small samples as their distributions are non-normal.

2. Unpaired or Independent t-test

The unpaired t-test is used to compare the means of two different groups of samples.

For example, we want to compare the male employees' average height to their average height. Of course, the number of males and females should be equal for this comparison. This is where an unpaired or independent t-test is used.

Here's the formula to calculate the t-statistic for a two-sample t-test:

Where,

• m_Aand m_B are the means of two different groups
• n_Aand n_B are the sample sizes
• S²is an estimator of the common variance of two samples, such as:

Here, the degree of freedom is n_A + n_B - 2.

We will follow the same logic we saw in a one-sample t-test to check if one group's average is significantly different from another group. That's right - we will compare the calculated t-statistic with the t-critical value.

3. Paired t-test

The paired sample t-test is quite intriguing. Here, we measure one group at two different times. We compare different means for a group at two different times or under two different conditions.

A certain manager realized that the productivity level of his employees was trending significantly downwards. This manager decided to conduct a training program for all his employees to increase their productivity levels. The formula to calculate the t-statistic for a paired t-test is:

Where,

• t = t-statistic
• m = mean of the group
• µ = theoretical value or population mean
• s = standard deviation of the group
• n = group size or sample size

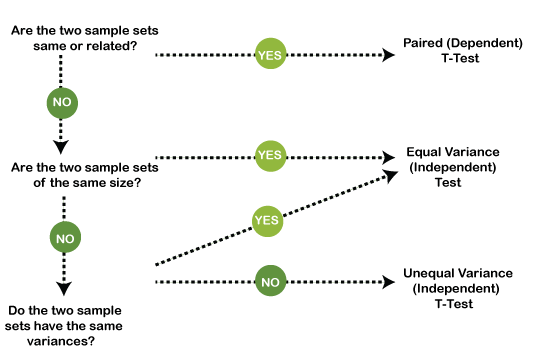
Calculating T-Tests

Calculating a t-test requires three key data values. They include the difference between the mean values from each data set called the mean difference, the standard deviation of each group, and the number of data values of each group.

The outcome of the t-test produces the t-value. This calculated t-value is then compared against a value obtained from a critical value table called the T-Distribution Table. This comparison helps determine the effect of chance alone on the difference and whether it is outside that chance range.

The t-test questions whether the difference between the groups represents a true difference in the study or possibly a meaningless random difference.

1. T-Distribution Tables
   The T-Distribution Table is available in one tail and two tail formats. The former is used to assess cases with a fixed value or range with a clear direction (positive or negative).
   For example, what is the probability of output value remaining below -3 or getting more than seven when rolling a pair of dice? The latter is used for range-bound analysis, such as asking if the coordinates fall between -2 and +2.
   The calculations can be performed with standard software programs that support the necessary statistical functions, like those found in MS Excel.
2. T-Values and Degrees of Freedom
   The t-test produces two values as its output, t-value and degrees of freedom.
   The t-value is a ratio of the difference between the mean of the two sample sets and the variation within the sample sets. While the numerator value (the difference between the mean of the two sample sets) is straightforward to calculate, the denominator (the variation within the sample sets) can become a bit complicated depending upon the type of data values involved. The denominator of the ratio is a measurement of the dispersion or variability. Higher values of the t-value, also called t-score, indicate a large difference between the two sample sets. The smaller the t-value, the more similarity exists between the two sample sets.
   • A large t-score indicates that the groups are different.
   • A small t-score indicates that the groups are similar.
   Degrees of freedom refers to the values in a study that can vary and are essential for assessing the null hypothesis's importance and validity. The computation of these values usually depends upon the number of data records available in the sample set.