Hall Effect

Hall Effect is defined as the phenomenon of the generation of a small voltage due to the deflection of charge carriers in a direction perpendicular to the direction of the electric filed and magnetic field.

The charge carriers are the electrons and holes. The electrons possess a negative charge, while holes possess a positive charge.

Hall Effect is generally observed in the conductor. Under the electric field (E) application, the electrons and holes drift and constitute a current. The magnetic field perpendicular to this electric field causes the deflection of the electrons and holes. Such deflection produces a small voltage in a direction perpendicular to the direction of the electric field and magnetic field.

The Hall Effect was discovered in 1879 by the physicist Edwin Hall.

Let's discuss how the electrons and holes result in the deflection under the electric and magnetic fields.

Drift of charge carriers in Electric and Magnetic fields

Let us consider the effect of the Electric field on an electron with charge q and mass m. We know that the electrons in a conductor are constantly moving in the absence of any field. Such movement is known as random motion. The same case applies to holes. Hence, we generally use the term 'charge carriers' for both the electrons and holes.

The energy for the movement of charge carriers in random motion comes from the temperature of the body. Thus, random motion is also called as thermal motion.

The movement of charge carriers in the random motion causes them to collide with each other. The collision occurs between the atoms of the lattice, impurities in the sample, and charge carriers themselves. But, the net average velocity is zero.

When the Electric field is applied, the charge carriers move in the x-direction with an average velocity in the same direction. There are large numbers of charge carriers and all are moving in the x-direction. The name given to such a motion with the collisions is termed as drift velocity. It is given by:

Jx=qnVx…(1)

Where,

Jxisthecurrentdensity
Vxisthedriftvelocity
qisthechargeofthecarrier
nisthenumberofchargecarriers

It can also be written as:

Jx=σEx
σistheconductivityofthematerial

It can be expressed as: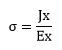

Hall Effect Experiment

As discussed, Hall Effect is generally carried on conductors. It is due to the presence of random charge carriers in the conductor.

Let's take a p-type semiconductor and apply a voltage between the two points (C and D) in the x-direction. It is shown below: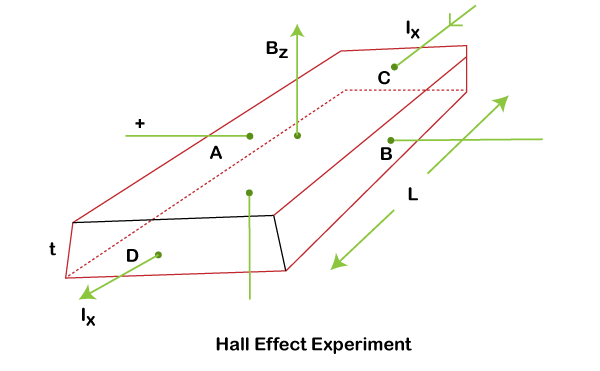

The p-type semiconductor consists of majority carriers' holes and minority carriers electrons. The application of voltage results in the drift of hole and the flow of current Ix. If a magnetic field B is applied in the z-direction, the holes in the x-direction are deflected. Such deflecting force due to the magnetic field experienced by a single hole can be written as: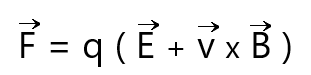

The above notation is expressed in the vector form. The force in the y-direction is:

Fy=(Ey-vxBz)…(2)

The impact of force on the hole causes it to gather the acceleration in the y-direction. The hole will no longer be able to move in the x-direction. A force in the y-direction needs to be applied so that the total force in the y-direction equals zero. It means that:

Ey=vxBz…(3)

The establishment of such electric field Ey is known as the 'Hall Effect.' The electric field can be calculated as: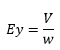

Here, V is called 'Hall Voltage.'

We know that Vx is the drift voltage, as discussed in equation 1. It is given by: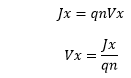

Putting the value of Vx in equation 3, we get: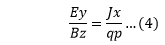

p is called as the carrier concentration of the semiconductor.

We have replaced n with p because we are considering the case of holes of a p-type semiconductor. If the semiconductor bar is n-type, the parameters will be -q and n instead of q and p.

We can write equation 4 as: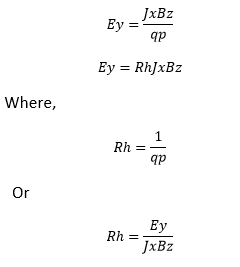

Here, Rh is called the Hall Coefficient.

Ey is called as the Hall Field.

Let's define other parameters using the above equations.

The number of holes can be calculated as: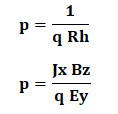

Putting the value of Ey = V/w and Jx = Ix / bw, we get: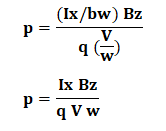

Here, bw is the area of the conductor.

Applications of Hall Effect

The Hall Effect is used to indicate the magnitude and presence of the magnetic field. Hence, it is preferred is various applications, such as sensors, DC motors, magnetometers, disk drives, speed detection, etc. Let's discuss some of the most common applications of the Hall Effect.

The applications of Hall Effect are listed below:

• Multiple sensors functioning
  The Hall sensors are used to detect the direction of the movement. When a rectangular semiconductor slab is placed in a magnetic field, the force causes by the field deflects the charge carriers. Such deflection helps to determine the movement of charge carriers in a particular direction.
  Some of the Hall Effect sensors come with a built-in voltage regulator and DC Amplifiers that improve the device's output voltage and hysteresis.
• Magnetometers
  The Hall Effect mechanism is used to find the magnetic field through the magnetometers. It is also a type of sensor that produces a voltage which is proportional to the applied magnetic field. But, it is used in applications where the presence of magnetic field strength is large.
• DC Motors
  The Hal Effect sensors are used in the brushless type DC motors. It is used instead of the brushes. The role of such sensors is to detect the position of the rotor or the permanent magnet.
• Disk Drives
  The Hall Effect sensors are used to detect the magnetic flux lines orthogonal to the Hard Disk Drive (HDD).

Advantages of Hall Effect

• Measures the magnetic field
  Hall Effect is used to determine the large magnetic fields. It can be measured with the help of the Hall Effect equation discussed above. The equation is:
  If the other parameters in the above equation (Voltage, the density of charge carriers) are known, we can easily calculate the magnetic field.
• Measures the carrier density
  By using other parameters (I, B, and q) and measuring the Hall voltage, the carrier density can be calculated using the Hall equation.
• Detection of the magnetic flux lines
  The Hall Effect sensors are various applications to detect the magnetic flux line, such as HDD.
• Charge Differentiation
  The Hall Effect parameters (Hall voltage) help us differentiate between the positive and negative charges. If the Hall Voltage is positive, it means that the mobile charge carriers are holes. Similarly, the negative Hall voltage depicts the presence of negative charge carriers.