How to calculate the square root?

In this article, we will discuss how to calculate the square root.

First, understand what square root is. So square root of a number is defined as a value, which on multiplication by itself gives the original number.

If the square of a number is x, the square root of that number will be the number multiplied by itself. For example, the square root of 625 is 25. If we multiply 25 two times, we get 625. It is easy to find the square root of such numbers, but it is tricky to find the square root for an imperfect square like 3, 5, 7, etc.

Mathematically, the square root of a number can be written as y = √a, which means 'y' is equal to the square root of a, where a is any natural number. It can also be expressed as y² = a.

The '√' symbol is called as the 'radical symbol' that is used to represent the root of numbers. The number or expression under it is called the radicand.

Properties

The properties of square root are listed as follows:

• The values of two square roots can be multiplied together, such as if we multiply √2 with √3, then we will get √6.
• If a number is a perfect square, then there exists a perfect square root.
• If a number ends with 2, 3, 7, or 8, i.e., if the mentioned digits are at the unit place of a number, then the perfect square root does not exist.
• The square root of any negative number is not defined.
• If a number ends with 1, 4, 5, 6, or 9, i.e., if the mentioned digits are at the unit place of a number, then the corresponding number will have a square root.
• On multiplying two square roots, the result should be a radical number. As an instance, if √7 is multiplied by √7, the obtained result will be 7.
• If a number is ending with an even number of zero's (0's), then the corresponding number can have a square root.

How to find the square root

There are various methods to calculate the square root of a number. Some are listed as follows -

• Prime factorization method
• Long division method
• Number line method
• Repeated subtraction method
• Average method
• Guess and check method

To calculate the square root of any number, first, we have to find whether the specific number is a perfect square or an imperfect square. We can use the prime-factorization method to calculate the square root, if the given number is a perfect square, i.e., 4, 9, 16, 25, 36, 49, 81, etc.

But if the given number is an imperfect square, i.e., 11, 13, 14, 15, etc., then we have to use the long division method to calculate the square root.

Now, let's understand the methods of calculating the square root.

Calculating square root by Prime-factorization method

It is easy to calculate the square root of a perfect square number. There are some examples of calculating the square root of some perfect square numbers shown below -

As shown above, we can calculate the square roots of perfect square numbers by the prime-factorization method.

Calculating square root by repeated subtraction method

This method is also used to find the square root of perfect square numbers. In this method, we have to continuously subtract the number (whose square root is to be calculated) by the consecutive odd number until the difference is zero.

The number of subtractions gives the square root of the number.

Let's understand it with some examples.

Example1: Suppose we have to find the square root of 25, which is a perfect square number. Then the process of finding the square root of 25 using the repeated subtraction method is given as follows -

25 - 1 = 24
24 - 3 = 21
21 - 5 = 16
16 - 7 = 9
9 - 9 = 0
So, the number of subtractions is 5. Therefore, the square root of 25 is 5.

Example2: Suppose we have to find the square root of 16, which is a perfect square number. Then the process of finding the square root of 16 using the repeated subtraction method is given as follows -

16 - 1 = 15
15 - 3 = 12
12 - 5 = 7
7 - 7 = 0
So, the number of subtractions is 4. Therefore, the square root of 16 is 4.

This method is easy but long for large numbers. This method is time-consuming to find square root for large numbers as there will be multiple steps required.

Calculating square root by average method

This method can be used to find the square root of whole numbers upto a few decimal places. In this method, the average concept is used to find the square root of the given decimal number. Now let's understand it using some examples.

Example: Find the square root of 5 by the average method.

Solution: The process of finding the square root of 5 using the average method is given as follows -

Step1: First, we have to check the perfect squares just below 5 and above 5. So, in this case, the perfect square above 5 is 9, and the perfect square just below 5 is 4.

Step2: Now, we have to write the square root of the perfect square of both numbers. So,
√4 =2, and
√9 = 3

Step3: Number 5 lies between 4 and 9, so it is clear that the square root of 5 will lie in between the square root of 4, i.e., 2, and the square root of 9, i.e., 3.
2² < 5 < 3²
Or, 2 < square root of 5 < 3

Step4: Now, divide 5 by 2. So,

5/2 = 2.5

Step5: Now, find the average of quotient and divisor in step 4. Here, the divisor is 2, and the quotient is 2.5.

So, (2 + 2.5)/2 = 4.5/2 = 2.25

Check whether the square of 2.25 is equal to 5 or not.

So, 2.25 * 2.25 = 5.062. If it is accurate for you, then you can stop it. Otherwise, you can repeat steps 4 and 5.

Value 2.25 is almost closer to the square root of 5, so we can select the same.

Calculating square root by Guess and check method

In this method, a number's square root is determined by finding the square numbers between which the given number lies. Here, the trial and error method is used to determine the square root. Now, let's understand it with an example.

Example: Find the square root of 7 with the Guess and check method.

Solution: The process of finding the square root of 7 using the Guess and check method is given as follows -

Number 7 lies between two square numbers that are 4 and 9, where the square root of 4 is 2, and the square root of 9 is 3. Therefore, the square root of 7 will be in between 2 and 3.

Let's assume 2.5 as the square root of 7, then
2.5 x 2.5 = 6.25, which is smaller than 7.

Assume 2.6 as the square root of 7, then
2.6 x 2.6 = 6.76, which is also smaller than 7.

Now, take 2.7 as the square root of 7, then
2.7 x 2.7 = 7.29, which is more than 7.

So, from the above calculations and results, it is clear that the square root of 7 will lie between 2.6 and 2.7
So, let's assume 2.65 as the square root of 7,
2.65 x 2.65 = 7.022, Which is approximately equal to 7
Therefore, from the above calculations, the square root of 7 is approximately 2.65. We can continue the process for the expected results.

Calculating square root by Long division method

To find the square root of imperfect squares is little tricky. The long division method can be used to calculate the square root of imperfect numbers. The long division method is little long but easy. It is the most suitable method to find the square root.

Example1: Find the square root of 529 with the help of the Long division method.

Solution: The step by step process of finding the square root of 529 is given as follows:

Step1: First, place the bar over the pairs of the given number starting from the right-hand side or unit place of the number. In case, as given, the total number of digits is 3, i.e., odd, so we also have to place the bar over the leftmost digit. For example: If the number is 7469, then it will be written as 74 69. In our case, 529 will be written as 5 29 as shown below -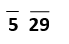

Step2: In the second step, we have to take the largest number as the divisor whose square is less than or equal to the number at the extreme left. The digit on the extreme left is considered a dividend, we have to divide and write the quotient.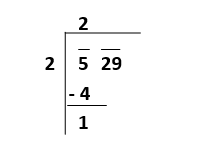

In this case, 2 is the divisor, 5 is the dividend, the quotient is 2, and the remainder is 1.

Step3: In this step, now we bring down the number under the bar and place it to the remainder's right side. In this case, we have to bring down the 29, and now 29 is our new dividend.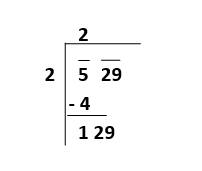

Step4: Now, in this step, we have to double the value of the quotient, and the new value will be our next divisor. We have to write this value together with an empty blank space on its right side. The process is shown below: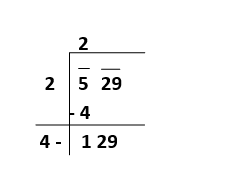

Step5: In this step, we have to take a number succeeding 4 to get a two-digit number such that when the two-digit number is multiplied by the number taken, the product is less than the new dividend. We can understand it via an example. Suppose if we take digit 3, then the new number will be 43. Now, 43 will be the divisor, and when it is multiplied by the number taken that is 3, we will get 43 x 3 = 129, which is equal to the given dividend.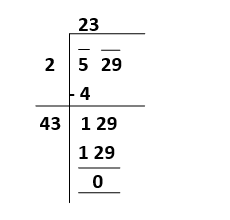

As the remainder is 0, and we have no number left for division. So, the square root of 529 is 23. To understand it more clear, let's see another example.

Example2: Find the square root of 2025 with the help of the Long division method.

Solution: In this example, we are not stating any step and showing the direct process of the problem.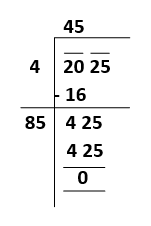

So the remainder is 0, and we have no number left for division. So, the square root of 2025 is 45.

Values of squares and square roots from 1 to 15

We are showing the values of the squares and square roots of the numbers from 1 to 15. The values are tabulated as follows: