Map Coloring in PrologIn mathematics, the famous problem was coloring adjacent planar regions. Two adjacent regions cannot have the same color no matter whatever color we choose. Two regions which share some boundary line are considered adjacent to each other. In the following map, the region is shown by some numerical names. 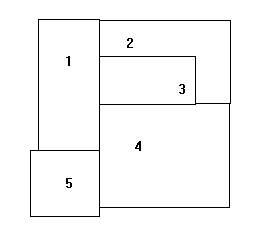
The above numerical name shows which regions are adjacent. Now we are going to consider the following graph: 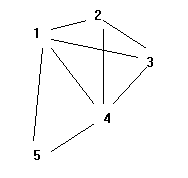
In the above graph, the original boundaries are erased. Now, we have an arc between the two regions name. The arc shows that both regions are adjacent in the original drawing. All the original adjacency information is conveyed by the adjacency graph. Using the following facts or unit clause, the adjacent information can represent in Prolog. In prolog, if we load these clauses, we will get the following behavior for some goals. In prolog, one could declare coloring for the regions. It will also use unit clauses. Here 'x' and 'y' colorings are encoded. In prolog, two adjacent regions which have the same color show the definition of conflictive coloring. The following example shows the prolog rule or clause to that effect. Prolog distinguishes the two definitions of 'conflict'. 1st definition defines 1 logical parameter. The 2nd definition defines 3 parameters. Now we have, The above example shows that region 2 and region 4 both are adjacent. It also shows that regions 2 and 4 both are blue. The consequences of prolog program are shown by grounded instance conflict(2, 4, y). One way to demonstrate such a consequence is to draw a program clause tree. In which, root of the tree contains the consequence, to branch the tree, it uses the clause of the program, and lastly, it will produce a finite tree which has all true leaves. Using the fully grounded instance of the clause, we can construct the clause tree, which is shown as follows: 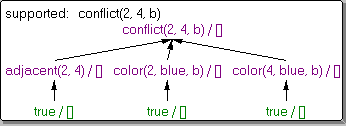
In the above tree, the bottom leftmost branch corresponds to the unit clause. adjacent(2,4) In prolog, this branch is equivalent to the clauseadjacent(2,4) :- true In prolog, the consequence of the program is not shown by 'conflict(1, 3, b)' because we can construct a finite clause tree using grounded clauses of P, which contains all 'true' leaves. Likewise, a consequence of the program is shown by 'conflict(a)'. To compute all possible colorings, we will develop a program in prolog. The famous four-color conjecture states that to color regions of the tree, we don't require more than four colors. The following example shows that we require at least four colors: 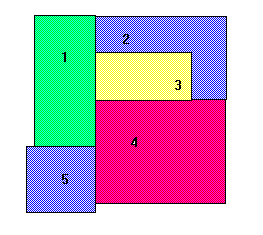
Next TopicTwo Factorial Definitions
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









