Unification in PrologWe will give a goal to evaluate and Prolog will work through the clauses in the database. In this, Prolog attempts to match the goal with each clause. The matching process works from left to right. The goal will fail if no match is found. If a match is found, the action will take. Prolog uses the unification technique, and it is a very general form of matching technique. In unification, one or more variables being given value to make the two call terms identical. This process is called binding the variables to values. For example, Prolog can unify the terms cat(A), and cat(mary) by binding variable A to atom mary that means we are giving the value mary to variable A. Prolog can unify person(Kevin, dane) and person(L, S) by binding L and S to atom kevin and dane, respectively. In starting, all variables have no value. In unification, once a variable bound to the value, it can be made unbound again and then perhaps be bound to a new value using the backtracking. Unifying Call TermsIn the following, flowchart can summarize the process. 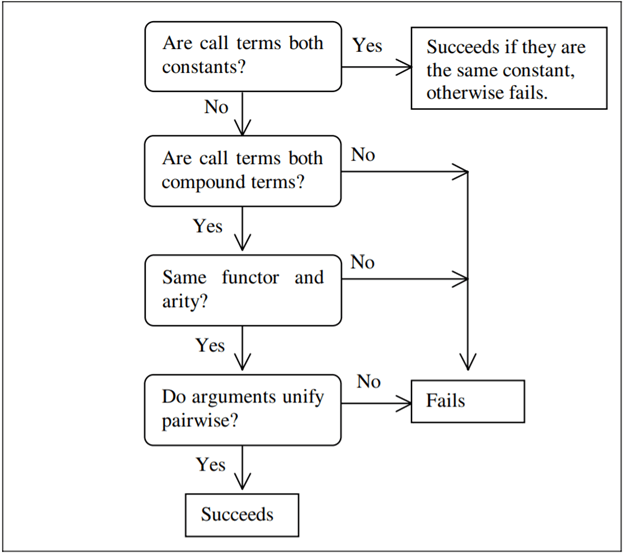
To consider this, we have three cases. In the first case, an atom is unified with another atom, and it is the easiest way. If two atoms are same, this will only succeed, so
In the second case, an atom is unified with a compound term like dane with likes(Kevin, henry). This second case always fails. In the third case, the two compound terms are unified, and it the most common case. For example dog(A) with likes(kevin, B) or likes(A, B) with likes(Kevin, henry). In two compound terms, if functor and arity are same, then the unification fails. Predicate is the same, so unifying dog(A) and likes(Kevin, B) fail. Same Functor and arity unify the two compound terms like parent(A, B, C) with the head parent(Kevin, tom, 30). It requires the head and clause arguments, which are unified 'pairwise', and it will work from left to right. In the two compound terms, the first arguments are unified, and then their second arguments are unified as so on. So, variable A is unified with atom kevin, then variable B with tom, and then C with 30. If all pairs of arguments in the two compound terms unify the unification, it will succeed just like in this case. It fails if not. The compound term has any kind of argument like variables, list, numbers, atoms, and compound terms. The following example shows some typical unification: Repeated VariablesIn a compound term, if a variable appears more than once, it will become the slightly more complicated case. The above has two compound terms in which the first argument is unified successfully. So, the A bound to canada. In the first compound term, all other values of A are also bound to canada. When the two second arguments are examined by Prolog, they are no longer A and cat but canada and cat. These atoms are different, and Prolog fails to unify. All bound variables are replaced by their value before Prolog unified any pair of arguments. A successful unification is shown by the following example, and it involves repeated variables. The following example describes a repeated variable in one of the arguments in the compound term. The variable L unifies with atom male, and variable S unifies with atom female. Now the two third arguments are unified by the Prolog, i.e., mypred(A, A, B) and mypred( no, yes, maybe). Firstly variable A unifies with atom no. The variable A successfully bound to no so it will succeed. Now, Prolog compares the two second arguments. As A is bound to no, instead of A and yes the second arguments are now no and yes, so unification fails. In the following example, unification succeeds because the second argument mypred is now no rather than yes.
Next TopicEvaluating Goals
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









