Towers of Hanoi Puzzle in Prolog

We can move the disks to another rod, using the tower of Hanoi puzzle. The movement goes left to right using the center peg. This center peg is like an auxiliary holding peg.

It contains three rods and the different sizes of disks. In this puzzle, at a time, only one disk can be moved. These disks are placed in ascending order that means the smallest disk places upon the largest disk.

The following image contains 3 disks. In 7 moves, the following puzzle can be solved.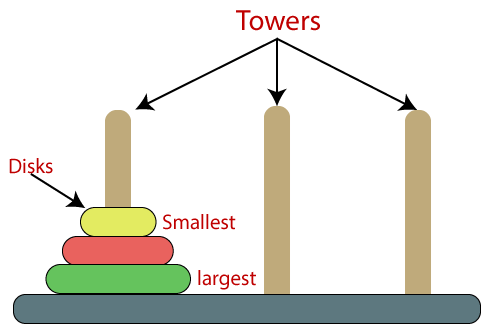

To solve the puzzle, the following recursive prolog program is as follows. This program contains two clauses.

The variables which begin with an underscore or filled in by '_' are known as 'don't care' variables. In prolog, any structure can freely match by these variables.

The following steps are shown when case N=3 is solved by the prolog.

In the program, the movement of a single disk can be described by the first clause. How the solution will recursively obtain is declared by the second clause. In the second clause, N=3, A=left, B=right, and C=center accounts.

The reading of this declarative clause is correct. The declarative interpretation of recursive clause is closely related to the procedural reading. The following code shows the procedural interpretation:

The declarative readings for N=2 are as follows:

In the above code, the body of last two implications is substituted for the heads. The prolog goal generates the solution, and one can see it.

In prolog, the three major operations are described as follows:

1. The head of a goal matches against the goals.
2. A new sequence of goals becomes the body of the rule repeatedly. Until
3. We take some simple action, or some condition is satisfied.