Types of Triangles

In mathematics, a triangle is one of the basic shapes used for educational purposes. In simple terms, a triangle refers to a polygon or a particular structure that has three sides. However, it can be of different shapes, and hence there are different types of triangles.

Here, we are discussing various types of triangles along with their definitions. Before discussing triangle types, let us first understand the definition of a triangle, including the general properties:

What is the Triangle?

As the name suggests, a triangle refers to a 2D (two-dimensional) shape closed by joining the three sides. In other words, a triangle is defined as a polygon containing three angles, three corners, and three vertices connected to create a closed shape.

The term 'triangle' is derived from the Latin word 'triangulus' that means 'three-cornered'. A triangle sign (∆) is used for denoting a triangle while solving or calculating relevant questions.

The following diagrams, A and B, are the basic examples of triangles:

Note: A triangle always has three sides and three angles, independent of its shape. Also, the sum of the three angles (inner angles) of any triangle will always add up to 180 degrees, known as the 'angle sum property of the triangle'.

Properties of Triangle

A triangle has many properties. Some of the common properties of a triangle are listed below:

• Every triangle includes three angles, three sides, and three vertices.
• A triangle is a two-dimensional polygon.
• The addition of any two sides' lengths in a triangle is always more than the third side's length.
• The perimeter of a triangle is equal to the addition of the length of the three sides.
• The product of the triangle base and the height gives the area of a triangle.

Types of Triangles

In particular, triangles are shapes that join three sides and three corresponding angles. However, there are generally six types of triangles, and each type has a specific name and characteristics. The type of triangle is defined based on the length of its sizes and different angles. Therefore, triangles are mainly divided into the following two types:

• Triangles based on sides
• Triangles based on angles

Let us discuss each type in detail:

Classification of Triangles based on their Sides

According to the length of the triangles' sizes, they are classified into the following three types:

• Scalenes
• Isosceles
• Equilaterals

Let us now understand each type:

Scalene Triangle

A scalene triangle refers to a triangle in which all sides are of different lengths. In such triangles, the length of each side is not equal to any other side. Also, there will be different interior angles in this type of triangle.

The following diagram is an example of the scalene triangle, where all side lengths and interior angles seem to be unequal.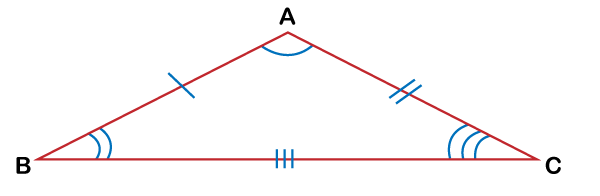

Isosceles Triangle

An isosceles triangle refers to a type of triangle in which the lengths of any two sides are equal. Additionally, the angles that lie in the opposite of the equal sides are of equal lengths. This means a triangle typically contains two equal sides and two equal angles.

The following diagram is an example of the isosceles triangle where two side lengths and opposite angles are equal.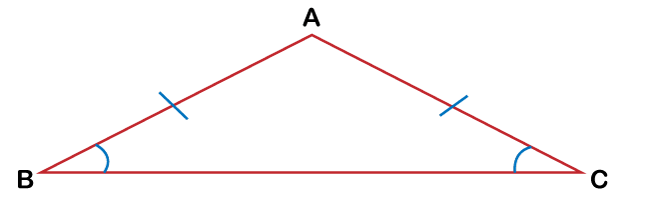

Equilateral Triangle

An equilateral triangle refers to a type of triangle that has all equal sides. Additionally, the three interior angles are also equal. In this triangle, each interior angle is equal to 60 degrees. Because all three angles of an equilateral triangle are equal, this triangle type is also called an equilateral triangle.

It is important to note that an equilateral triangle's lengths do not relate or depend on the interior angles and vice versa.

The following diagram is an example of the equilateral triangle where all three sides are of equal lengths, and all three interior angles have a measure of 60 degrees, i.e., AB = BC = CA and ∠ ABC =∠ ACB = ∠ BAC.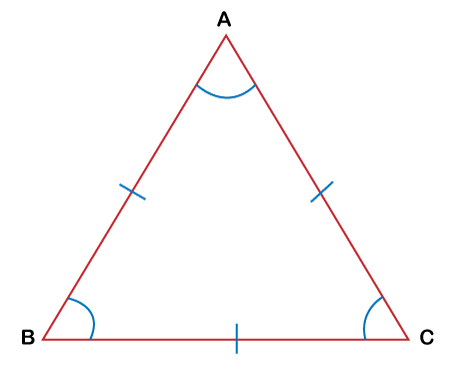

Classification of Triangles based on their Angles

According to the interior angles of the triangles, they are classified into the following three types:

• Acute-angled Triangle
• Obtuse-angled Triangle
• Right-angled Triangle

Let us now understand each type separately:

Acute-angled Triangle

A triangle that contains all three interior angles as acute is known as an acute-angled triangle or acute triangle. In simple terms, an acute triangle is a triangle with each interior angle less than 90 degrees that include all three angles.

The following diagram is an example of an acute-angled triangle in which all interior angles (a, b, and c) are below 90 degrees.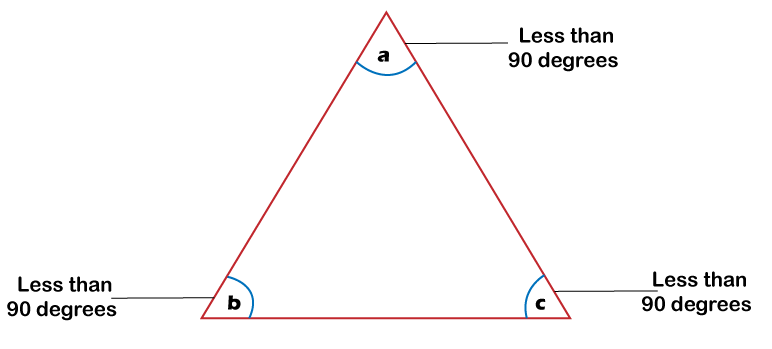

Obtuse-angled Triangle

A triangle with an obtuse angle at one of the three interior angles is defined as an obtuse-angled triangle (also called an obtuse triangle). In other words, the obtuse triangle is the triangle in which one of the three interior angles is above 90 degrees.

The following diagram is an example of the obtuse-angled triangle where one angle (a) is more than 90 degrees (obtuse) while the others (b and c) are less than 90 degrees (acute).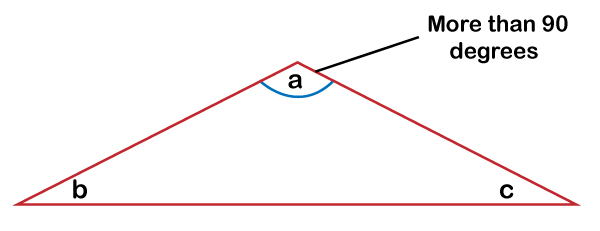

Right-angled Triangle

The right-angled triangle refers to the triangle with one of three interior angles equal to 90 degrees. Additionally, the side that lies at the opposite of the right angle (90-degree angle) is the longest side of all three sides. This longest side is referred to as the 'hypotenuse'.

It should be noted that the right-angled triangle is different from the isosceles triangle. A right-angled triangle always has one of the three interior angles equal to 90 degrees, while the isosceles triangle has no such condition.

The following diagram is an example of the right-angled triangle where one angle (a) among all three angles is 90 degrees while the other two angles (b and c) are acute.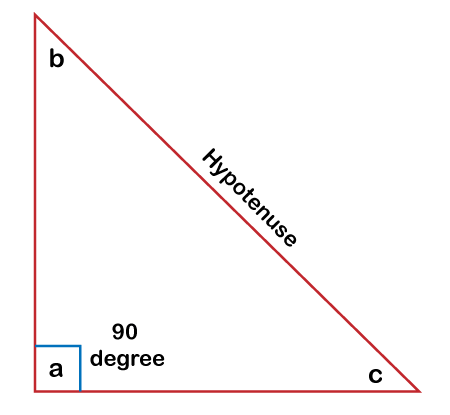

Examples of Triangles

We all know that triangles are one of the most important shapes in trigonometry and geometric study. Apart from this, triangles also have many general-life applications. Some of the real-life examples of triangles are as follows:

• When pyramids are drawn on paper or seen from a distance, they form like a triangle shape.
• The Eiffel Tower forms a triangular shape in photos and drawn structures.
• The trusses of roofs and bridges are generally constructed in a triangle shape because they are considered the strongest type of shape.
• Sandwiches are the most common real-life examples of triangles.
• The Bermuda Triangle is a very popular triangular region located in the Atlantic Ocean. Any aircraft or ship passing through this area is swallowed. It is a mysterious triangular area.