Difference between Circle and Sphere

What is a Circle?

A circle is a closed, two-dimensional shape or figure in which every intersection of the plane is equally spaced out from a central point or dot. Additionally, the center of a circle ejects a rotational symmetry for each angle.

A particular kind of line is drawn to create a circle. Every point along a circular line must be evenly spaced out from a fixed point on a plane for the line to be considered round. The plains are divided into inner and outer parts by a closed circle that forms the structure. One of the numerous features of a circle is its radius, diameter, chord, center, circumference, and tangent.

The letter "r", which stands for the radius of that circular line, is used to designate the lines that join the lines from a particular circular line to its center. A circle having a number of points and a constant sum of the separation between two fixed points in a plane is referred to as an ellipse. The terms "focus" and "center", which refer to these two fixed positions, are the same in the case of a circle. The edges of a triangle are defined by three groups of points in the inner circle that are not present in the same direction. Clocks, discs, and wheels are some instances of circles.

A circle, when used literally, is a ring; the word "circle" is derived from the Greek word "Kirkos". A circle is a collection of points with the property that each point is at a constant distance from a certain position on the planar surface. This loop divides the plains into two sections with closed ends and separates the inner and outer sectors.

A circle is one of the most basic geometric shapes, and it is commonly used in mathematics and everyday life. The circle has a few key properties that make it unique, including its circumference, diameter, radius, and area.

The circumference of a circle is its perimeter which means a boundary enclosing a figure. It is calculated using the formula C = 2?r, where ? (pi) is a mathematical constant approximating 3.14. The diameter of a circle is the distance across its widest point, passing through its center. The radius is essentially half the size of the diameter. The distance from a circle's center to any point on its periphery is its radius, to sum things up. The formula A = ?r^2 is used to compute the area of a circle, which is the amount of space enclosed in the circle itself.

There are many real-world applications of circles, such as the wheels on a car or the shape of a pizza. They are also used in many mathematical formulas, such as trigonometry and calculus. In addition, circles are used in art and design, such as in creating mandalas or designing logos.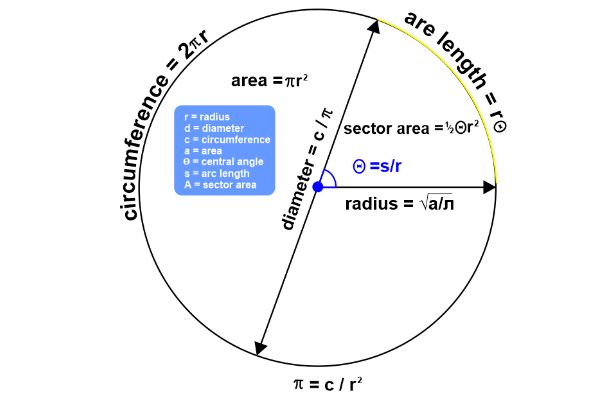

Properties of a Circle

A circle is a two-dimensional geometric shape consisting of points equidistant from a single point known as the center. The radius of a circle is the gap between its center and any point along its circumference. The diameter is the distance across the circle through its center, which is twice the size of the radius. One of the fundamental properties of a circle is that it has constant curvature. This means that no matter where you measure the curvature of a circle, it will always be the same. Another property of a circle is that the circumference, which is the distance around the circle, is proportional to the diameter, and the ratio of the circumference to the diameter is always the same, approximately 3.14, known as pi.

Another property of a circle is that it has an infinite number of tangents. A tangent is a line that only crosses (or touches) the circle at its circumference once and is perpendicular to the radius at that location. In addition, at the point of tangency, a 90-degree angle exists between the tangent line and the radius. Another important property of a circle is that the chords are equidistant from the center. A line segment that joins two locations on the circumference of the circle is known as a chord.

What is a Sphere?

A sphere is a three-dimensional geometrical thing with surface points that are equally spread out from one another. The radius is the distance between the surface and the common point, also known as the sphere's center of mass.

A sphere has three dimensions instead of two dimensions, as in a circle. At any axes, every point on a sphere is equal in distance from its center. The sphere's volume, surface area, and radius are simple to determine. The line connecting the farthest edge points is called the sphere's diameter. The spherical has absolutely no circumference. Little circles and hemispheres can be found inside the sphere. A few typical instances of spheres include water droplets, marbles, and soccer balls. A sphere, as opposed to a circle, is a typical three-dimensional shape. A sphere's points will all have centers that are equal in size. It is frequently used to quickly determine the radius, surface area, and surface area's dimensions. A sphere's diameter is a straight line that connects the two opposing ends of the circumference and runs through the object's center. A sphere is created by joining together numerous smaller circles and hemispheres. Spheres include things like footballs, oranges, eyeballs, and many others.

A sphere is considered to be a three-dimensional version of a circle, and it has many unique properties that make it a fascinating shape to study.

Like a circle, a sphere has a few key properties that make it unique. The surface area of a sphere is the total area of its outer surface, and it is calculated using the formula A = 4?r�, where r is the sphere's radius. The formula V = ????r� is used to compute the volume of a sphere, which is the amount of space engulfed inside the sphere. The diameter of a sphere is the distance across its widest point, passing through its center. Finally, the radius of a sphere is the distance from its center to any point on its outer edge.

Spheres are used in many real-world applications, such as creating ball bearings, designing mirrors, and modeling planets. They are also used in mathematical formulas, such as calculating a planet's volume or the amount of air in a balloon.

Another interesting property of spheres is their symmetry. A sphere has infinite rotational symmetry, meaning it looks the same no matter how much it is rotated around its center.

Types of Spheres

Solid Sphere: A solid sphere is a solid object shaped like a sphere. The same substance that makes up a solid spherical also fills it.
Hollow Sphere: A hollow sphere is created when a solid sphere has large solid parts removed from the center, leaving a spherical shell behind.

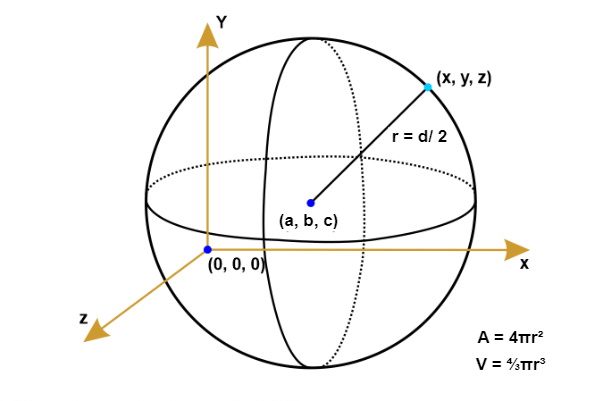
Properties of a Sphere

A sphere is a three-dimensional geometric shape generated by continuously rotating a circle around its diameter. Like circles, spheres have a center point, equidistant from all points on the sphere's surface. A radius of a sphere is exactly one-half of the size of its diameter. One of the fundamental properties of a sphere is that it has constant curvature, just like a circle. This means that any individual section of a sphere is a circle when considering a two-dimensional shape.

The surface area of a sphere is the total area that the surface of the sphere covers, and it is given by the formula 4?r�, where r is the sphere's radius. Another important property of a sphere is its volume, which is the space inside it. The volume of a sphere is calculated using the formula ????r�. This means that if you double the radius of a sphere, its surface area and volume will increase by a factor of 4.

Similar to circles, spheres also have an infinite number of tangents. The tangent line and radius at the point of tangency form a 90-degree angle, much like in circles. In addition to tangents, spheres also have great circles. A great circle is a circle that intersects the sphere in such a way that the circle's center coincides with the center of the sphere. Great circles are also the largest ones drawn on a sphere.

A sphere ejects a rotational symmetry enclosing the axis that goes through the center. This means that if you rotate a sphere around its axis, it will look the same from any angle. This symmetry property of spheres is why they are used in many real-world applications, such as optics, where lenses and mirrors are designed using spherical shapes.

Another interesting property of a sphere is its ability to roll smoothly without slipping. This is because, as the sphere rolls, each point on its outer surface moves at the same speed. As a result, there is no sliding friction, which makes it easier for the sphere to roll smoothly. This property makes spheres ideal for creating objects that need to be symmetrical, such as creating crystal balls or designing sports equipment.

Key Differences between a Circle and a Sphere

Circle	Sphere
A circle is a 2-d figure.	A sphere is a 3-d object.
A circle has an area and a circumference as its boundary.	A sphere has an area and a volume instead of a circumference.
A circle's circumference is equal to 2?r, and the area of a circle is equal to ?r ^2.	A sphere's volume is equal to (4/3)?r ^3, and the surface area of a sphere is 4?r ^2
The standard equation for a circle is (x-a) ^2 + (y-b) ^2 = r ^2. Here, the center of a circle is at (a, b).	The standard formula for a sphere is (x-a) ^2 + (y-b) ^2 + (z-c) ^2 = r ^2. Here, the center of a sphere is at (a, b, c).
All of the points on a circle are equally spaced apart from the center along a plane.	All of the points on a sphere are equally spaced apart from the center along any axes.
In the case of a circle, we can only calculate the area but not the volume.	For a sphere, we can compute both the surface area and the volume.
A circle is a figure.	A sphere is an object.
A circle is a flat shape that lies entirely on a plane. It has no thickness, and all its points are equidistant from the center.	The three-dimensional shape of a sphere, on the other hand, is round and has a curved surface. It is symmetrical in all directions and has a fixed center.
A circle does not have an axis of rotation since it is a two-dimensional shape.	In contrast, a sphere has an axis of rotation, which is the line passing through the sphere's center and perpendicular to its surface.
A line that only touches a circle once is said to be tangent. A tangent can be drawn at any point on its circumference in a circle.	In contrast, in a sphere, a tangent can only be drawn at any single point where the tangent plane intersects the sphere's surface.

Conclusion

Circles and spheres are the most basic and important shapes in mathematics and the real world. Circles are two-dimensional shapes that are perfectly round and have a set of points that are equidistant from their center. They have unique properties such as circumference, diameter, radius, and area and are used in many real-world applications, such as in creating wheels or designing logos. Spheres, on the other hand, are three-dimensional shapes that are perfectly round and have a set of points equidistant from their center. They have unique properties such as surface area, volume, diameter, and radius and are used in many real-world applications, such as in creating ball bearings or modeling planets. Both shapes have interesting properties that make them ideal for various applications, such as the ability of spheres to roll smoothly without slipping and their infinite rotational symmetry.

Studying circles and spheres is important for mathematical and scientific purposes and practical applications in various fields, such as engineering, architecture, and design. Understanding the properties and behaviors of these shapes can help us create better and more efficient products, structures, and systems.

From the circular motifs in Islamic art to the use of spheres in modern sculpture, these shapes have been used to create visually stunning works of art and design.

Overall, the circle and sphere are fundamental shapes that are both simple and complex simultaneously. Their unique properties and behaviors make them essential in mathematics, science, and the real world. Understanding these shapes and their properties can help us solve problems, design better products and structures, and appreciate their beauty and symmetry in art and design.

Next TopicDifference between

← prev next →