Difference Between Mean and Median

Mathematics frequently makes use of terms such as mean and median. Mean is similar to an average of a particular number. The Mean is calculated by putting all the numbers together and dividing the result by the total number of digits. However, the median delivers, if ever, the median value from the whole data collection.

The median is calculated by combining the two intermediate values and dividing the result by two. The three average metrics of mean, median, and mode illustrate how much the data differs from the Mean or the average. These approaches are frequently employed in statistics, with the data mean value approach being the most popular.

Mean of Definition

The Mean is calculated by dividing the total number of observations in the collection by the total number of all the data points. When discussing the mean or average height of a group of five people, for instance, we would total the five individuals' heights and divide that amount by five to get at the Mean. Utilizing statistics is one of the most widely used methods of measuring a central pattern.

The mean value in a data collection is determined by dividing the total number of values by the aggregate of all the values in the data collection.

• It is frequently described as "average."
• It is represented by the letter "x?."
• Mean is a critical concept in finance and is utilized in several financial areas, including business assessment.

The Formula for the Mean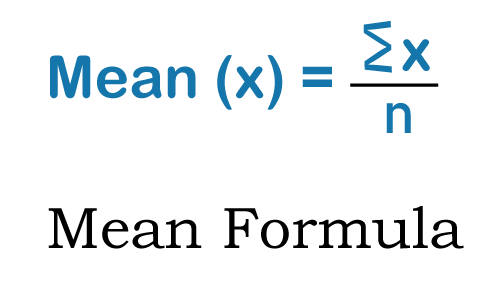

The average number of observations is calculated by dividing the total observations by their aggregate. It will be useful in resolving a majority of arithmetic mean-related problems. It is possible to describe the mean formula of the provided observations as,

Formula for the Mean = (Sum of Observations) ÷(Total Numbers of Observations)

We also have a mean formula for data that has been grouped. This is written as

x? = Σ fx/N

where,

• x stands for the data collection's mean value.
• F stands for the frequency of the specific data.
• N stands for the Sum of Frequency.
• As a result, the average of all data points is what is meant by the term "Mean."

Type of Mean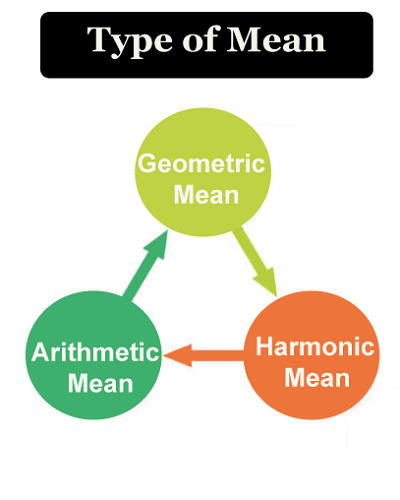

There are three main categories in which Mean can be categorized

• Geometric Mean
• Arithmetic Mean
• Harmonic Mean

Depending on the circumstances or problem presented, Statistics will use a different formula to calculate these three means.

1. Geometric Mean (GM)

The average number calculated by taking the nth root of the product of the n values in the data collection is the geometric mean. It's a term used to describe proportionate growth.

2. Arithmetic Mean (AM)

Common names for arithmetic Mean include Mean, simply an arithmetic average. All observations added together and divided by all observations equals the arithmetic mean.

3. Harmonic Mean (HM)

The harmonic Mean is the opposite of the numerical mean of the reciprocals.

Median of Definition

The median value in the data array set, known as the median, distinguishes the higher collection of data from the lower stage. Consequently, the data must be organized in ascending order before computing the median.

The Mean of the middle two digits in the data set must be determined once the data set has cardinality. However, these two techniques are frequently applied in combination. The median, together with the Mean and mode, is one of three measurements of central tendency.

• After organizing the data in ascending sequence, the median is the outcome.
• It is described as the location where half the data is more significant, and half the data is minor.
• It is a positional average since the median is determined using the data in the sequence's center.
• The median is considered to be the most detailed statistical statistic to determine.

The Formula for the Median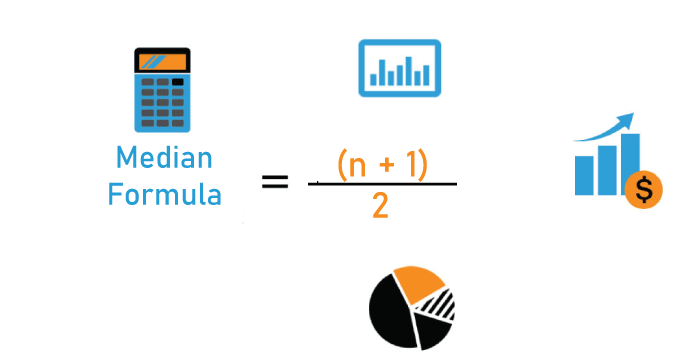

For the median to be computed, the data must be arranged in increasing or decreasing order. Obtain the total number of observations in the data after organizing it. If the number is odd, the median equals (n+1)/2.

If the integer is even, the two center values can be obtained using n/2 and (n/2) + 1. These two central words should be averaged out. The median method is presented below for even numbers.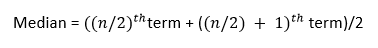

Difference Between Mean and Median

• Mean is straightforward and may be used with any even or odd data array collection. The median requires the data set to be organized in a descending or ascending sequence before calculation because it is a relatively sophisticated statistic.
• The median is typically used for data sets with skewed distribution, whereas the mean is generally used for normal distributions.
• The mean is easy to understand but needs more sturdiness since it occasionally fails to provide the user with accurate results for interpreting data and can sometimes contain outliers in the distributions. In contrast, the robustness of the median approach makes it more suitable for skewed distributions to determine the data set's central tendency, and it will provide the user with many more accurate findings than the mean.
• The total amount split by the number of observations is the only known formula for calculating the mean. Two distinct procedures are used to determine the median. One peculiar case is that the dataset's middle integers determine the median. The median of an even data set is obtained by choosing the central value between the two and dividing it by two. The following table explains the distinction between the mean and median.

Properties of Mean and Median

Mean's Properties

• For every collection of numerical data, the mean may be computed.
• When it comes to numerical data, there is only one mean.
• Because it considers every item in the data set, the mean is the most trustworthy indicator of central tendency.
• Exceptionally big or tiny data values influence the mean.
• The sum of the standard deviations between each observation is zero.
• The mean product with the number of things it is based on equals the total number of items provided.
• A collection of values' squared deviation from the mean is at its smallest.
• The actual mean may be used to replace each item from the original series, and the total of all those replacements will equal the sum of the individual things.
• The mean is not unaffected by the scale and origin changes.

Median's Properties

• Every data collection has a different median.
• While exceptionally big or tiny values occur, it is still a useful measure of central tendency since it is unaffected by them.
• It is not possible to use data with a qualitative component.
• If the data are ordinal, the median is utilized.
• A graphic method can be used to determine the median.
• Compared to the actual absolute deviations from any other observation in the data, the overall absolute deviations from the median are lower.

Use the Mean

When both of the following circumstances are met, the mean is applied

1. Data is scaled

Weight, height, temperature, and speed are examples of data with regular intervals.

2. Distribution is normal

Since the mean is susceptible to outliers in skewed distributions, you should only use it when the distribution is generally normal.

Use the Median

When one of two requirements is met, the median is utilized. When the

• Data is ordinal.
• The distribution is unusual or skewed.

Conclusion

The mode is an additional metric frequently employed to measure central tendency in addition to the mean and median. Using the three data collection techniques, an intelligent analyst will measure the central tendency. The analyses' discrepancies should be carefully studied for the data set to produce better and more accurate findings.

Even though the mode and median perform better analyses and discover better results than the mean, the mean is still the most appropriate indicator of central tendency, especially if the data set has a normal distribution and the data are typically skewed.