Difference Between Rectangle and Parallelogram

Mathematics is a fundamental area of science that deals with numbers, quantities, and forms. It is a global language that allows us to comprehend and catalog all aspects of the natural world, from the tiniest subatomic particles to the grandest cosmic architecture. Mathematical figures are geometrical shapes that are studied in mathematics. These shapes have properties described by mathematical formulas and equations, and they play a significant role in fields such as geometry, trigonometry, calculus, and physics.

Some of the most common mathematical figures include:

1. Circle: A circle is a closed shape with all points on its boundary equal to its center. Its properties include its radius, diameter, circumference, and area.
2. Triangle: A triangle is a three-sided polygon with three angles. Its properties include its side lengths, angles, perimeter, and area.
3. Square: A square is a four-sided polygon with all sides of equal length and all angles of 90 degrees. Its properties include its side length, perimeter, and area.
4. Rectangle: A rectangle is a four-sided polygon with opposite sides parallel and all angles of 90 degrees. Its properties include its length, width, perimeter, and area.
5. Trapezoid: A trapezoid is a four-sided polygon with one pair of parallel sides. Its properties include its bases, height, perimeter, and area.
6. Sphere: A sphere is a three-dimensional object with all points on its surface at an equal distance from its center. Its properties include its radius, diameter, surface area, and volume.
7. Cone: A cone is a three-dimensional object with a circular base and a curved surface that tapers to a point. Its properties include its height, radius, slant height, surface area, and volume.
8. Cylinder: A cylinder is a three-dimensional object with two parallel circular bases connected by a curved surface. Its properties include its height, radius, surface area, and volume.
9. Cube: A cube is a three-dimensional object with six square faces of equal size. Its properties include its side length, surface area, and volume.

These mathematical figures are not only crucial in mathematics, but they are also helpful in various fields such as architecture, engineering, and design. By understanding their properties and how they relate to each other, mathematicians and professionals can make more informed decisions and create more efficient and practical designs.

Geometric shapes offer various valuable applications in daily life, from specific activities like calculating distances to intricate engineering designs. We shall look at some of the most typical applications of geometric shapes in this post.

• First, basic geometric shapes like points, lines, and angles are employed to determine directions and measure distances. Geometric figures are used, for instance, to calculate the distance between two spots and the direction we need to travel when using a map or GPS. Similarly, geometric figures like angles and lines in construction and architecture determine the proportions and design of buildings and structures.
• Second, various disciplines like engineering, physics, and computer science employ geometric figures. For instance, engineers utilize geometric shapes to create buildings and bridges that endure various pressures and forces. Geometric shapes are used in physics to depict and compute the behavior of particles and waves. In computer science, image and form recognition algorithms, computer graphics, and animation all employ geometric shapes.
• Thirdly, geometric shapes are a subject of study and a tool for production in art and design. From complex geometric patterns in Islamic art to straightforward geometric forms in contemporary graphic design, artists and designers employ geometric shapes and patterns to produce visually attractive compositions.
• Finally, games and sports also make use of geometrical figures. For instance, the field is a rectangle in football, and the ball is spherical. Players must understand these forms' geometrical characteristics to move the ball and score goals. Similarly to this, the movement and positioning of pieces in games like chess and checkers are determined by geometric forms.

History of Study Geometry

When geometry initially became a discipline of study in antiquity, the study of rectangles and parallelograms began. Babylonia was one of the earliest civilizations to apply geometry to address construction and land measurement issues, followed by ancient Egypt.

The circle, probably discovered and used by the ancient Egyptians in approximately 2500 BCE, is the first known use of a geometric figure. The circle served as both a standard for measuring time and a representation of the sun for them.

Through the work of mathematicians like Euclid and Pythagoras, the Greeks made essential contributions to studying rectangles and parallelograms. One of the most important books in the history of geometry, Euclid's Elements, from the third century BCE, contains numerous crucial theorems on parallelograms and rectangles.

Islamic mathematicians played a significant role in developing trigonometry and applying algebraic techniques to studying geometry throughout the Middle Ages. Al-Khwarizmi's and Al-Kindi's writings had a significant impact on this.

Rectangle and parallelogram studies have remained a significant field of study in geometry even in the present day. The advent of analytic geometry in the 17th century opened up new directions for study in this area by enabling the use of algebra to solve geometric issues.

Rectangles and parallelograms are still important topics to master in geometry today since they are frequently used in the architecture, engineering, and computer graphics industries. Mathematicians worldwide continue to research and study the characteristics of these forms, and new findings and understandings are continually being discovered.

Rectangle

A rectangle is a four-sided polygon with opposite sides parallel and equal in length. The word "rectangle" comes from the Latin word "rectangular," which means "a right angle." The concept of a rectangle has been used in mathematics for thousands of years, and it is one of the most basic shapes studied in geometry.

The concept of a rectangle can be traced back to ancient civilizations such as the Babylonians, who used rectangles in their architectural designs. The Egyptians also used rectangles in their constructions, particularly in the design of their pyramids. In ancient Greece, the rectangle was studied extensively by mathematicians such as Euclid, who included it in his Elements, a textbook of geometry that is still used today.

The properties of a rectangle have been used in various fields throughout history. For example, rectangles are used in architecture to design buildings and structures. Many buildings, such as houses and offices, have rectangular floor plans. In art, rectangles are used as the basis for creating images, such as paintings and photographs. Rectangles are also commonly used in graphic and web design, as they provide a simple and clean shape that is easy to work with.

One of the most practical uses of rectangles is in furniture construction. Many pieces of furniture, such as tables and bookshelves, are designed with rectangular shapes. This is because rectangles provide a stable and balanced foundation for the furniture, making it easier to use and more aesthetically pleasing.

In mathematics, rectangles are studied extensively because of their many valuable properties. For example, the area of a rectangle is calculated by multiplying its length and width, which is a simple and widely used formula. Additionally, the perimeter of a rectangle is calculated by adding the length and width of the rectangle multiplied by two.

In conclusion, the rectangle is a simple yet essential shape used in various fields throughout history. Its practical uses, as well as its mathematical properties, make it a fundamental shape that is studied extensively in geometry and other related fields.

Parallelogram

A quadrilateral with two sets of parallel sides is a parallelogram. The Greek terms "para" and "gramma," which both mean "beside" and "line" or "letter," respectively, are the origin of the word "parallelogram." Parallelograms were initially employed in building constructions in ancient Egypt, where they were first discovered.

Parallelograms were frequently used to construct temples and other sacred buildings in ancient Egypt. Also, they were employed in constructing the pyramids and other imposing structures. The Egyptians were adept mathematicians who calculated the areas and volumes of various forms using parallelograms.

Parallelograms were a standard geometry tool among the Greeks, and Euclid explored them in great detail in his work "Elements." Parallelograms are described in this book by Euclid as quadrilaterals with opposing sides that are parallel and congruent. Also, he established other characteristics of parallelograms, including the unity of opposing angles and the diagonals' intersection.

Several ancient civilizations, including the Chinese and the Babylonians, also investigated parallelograms. They employed them to solve real-world engineering, architecture, and land surveying issues. Parallelograms are still employed in several disciplines, such as mathematics, geometry, physics, and engineering. In addition to calculating areas and volumes, they are frequently employed to address issues with force and motion. They are also used in planning bridges, buildings, and others.

A quadrilateral with two sets of parallel sides is called a parallelogram. It has the following mathematical characteristics:

• The opposing sides are parallel and congruent.
• Congruent angles are opposite angles.
• Diagonals cut each other in half.
• Three hundred sixty degrees are made up of all internal angles.

Parallelograms are helpful in a wide range of applications due to their characteristics, including:

• Calculating Area: Multiplying the base and the height will give you the area of a parallelogram.
• Calculating Volume: Parallelograms determine the volume of several objects, including prisms and cylinders.
• Engineering: Parallelograms design bridges and other structures to distribute weight and stress equally.

A specific kind of parallelogram with four right angles is a rectangle. They also possess different qualities like:

• The opposing sides are parallel and congruent.
• Right angles exist in every angle.
• The opposites are equivalent.

Rectangles are advantageous due to these characteristics in a wide range of contexts, including:

• Calculating Area: Finding the area of a rectangle involves multiplying its length by its width.
• Calculating Perimeter: The total of all a rectangle's sides, which can be computed using the formula 2(length + width), is the perimeter.
• Engineering: Rectangles are utilized to develop robust, sturdy structures such as windows, doors, and buildings.

Parallelograms and rectangles are employed in mathematics for geometric proofs and to teach students about ideas like angles, area, and volume, in addition to their practical uses.

Difference Between Rectangle and Parallelogram

Parallelograms and rectangles are both varieties of quadrilaterals, although they differ significantly in a few key ways.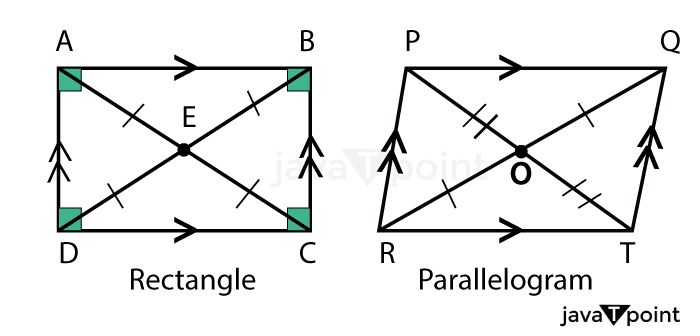

Which Is a Better "Shape": Rectangle or Parallelogram

Determining whether a rectangle or a parallelogram is a superior form is challenging because each has distinct qualities and applications. We must first define what we mean by "better "to analyze which form is superior.

When deciding which form is best for a particular work or goal, such as building a structure or creating a brand, the answer will rely on the details of that task. For instance, a rectangle would be preferable if we were developing a logo that must be instantly recognizable and symmetrical. On the other hand, a parallelogram may be a more helpful form if we create a structure with sloping walls.

Each of the two forms has a different set of attributes that make them distinct mathematically. In contrast to a parallelogram, which has four opposite sides that are parallel and congruent, a rectangle has four right angles on its four sides. Despite having the same number of sides and angles, the two shapes have different symmetry and congruency characteristics.

Rectangles are advantageous in many situations due to their extraordinary degree of symmetry. An easy way to make visually appealing layouts, for instance, is to divide a rectangle into halves or quarters in graphic design. Due to a rectangle's characteristics, determining its area and perimeter in mathematics is simple.

A parallelogram does, however, have certain benefits. It may be used to create geometric shapes and calculate area and perimeter due to its congruent sides and opposing angles. A diamond shape, for instance, may be made from a parallelogram and is frequently utilized in ornamental patterns.

Graphical Representation of The Figures

In geometry, the shapes of a rectangle and a parallelogram on a graph show various characteristics and connections between points and lines in the plane.

Rectangles and parallelograms can also depict regions or areas in the plane in coordinate geometry. A rectangular area of height h and width w, for instance, is represented by a rectangle with vertices at (0, 0), (0, h), (w, h), and (w, 0). This rectangle's area may be computed using the formula h x w. A parallelogram region with base length a and height b is represented as a parallelogram region with vertices at (0, 0), (a, b), (a+c, b+d), and (c, d). The base times the height of this parallelogram, or |a x b|, may be used to compute its area.

Conclusion

To summarize, parallelograms and rectangles are two kinds of quadrilaterals with similarities and significant distinctions. Parallelograms have opposing sides that are parallel and congruent, whereas rectangles have four right angles. Opposite angles and one pair of opposite sides are both parallelograms congruent. Whereas all the sides and angles of a rectangle are congruent.

Several applications in various domains, including architectural design, furniture design, engineering, and mathematics, result from the variation in geometric figures. Parallelograms are used to calculate the areas and volumes of three-dimensional objects, whereas rectangles are frequently utilized as a base for constructing structures and producing stable, perpendicular designs. Both forms are beneficial in various situations due to their distinctive qualities and uses. For studying geometry and utilizing these forms in various disciplines, it is crucial to comprehend the differences between rectangles and parallelograms.