Bellman-Ford Algorithm Java

In dynamic programming, there are many algorithms to find the shortest path in a graph. Some of them are Dijkstra's algorithm, BFS, DFS, Floyd, all-pair shortest path problem, and bidirectional algorithm. The most commonly used algorithm is Dijkstra's algorithm. The limitation of the algorithm is that it cannot be applied if the graph has negative edge weights. Another difference is that the Dijkstra algorithm looks only to the immediate neighbors of a vertex, Bellman-Ford goes through each edge in every iteration.

To overcome this problem, the Bellman-Ford algorithm can be applied. It deals with the negative edge weights. In this section, we will understand the Bellman-Ford algorithm with example and also implement the Bellman ford algorithm in a Java program.

Bellman-Ford Algorithm

It is a single-source shortest path (minimum weight) algorithm very similar to Dijkstra's algorithm. It can be applied in a graph if we want to find the shortest path. Note that it deals with the negative edge weights. The limitation of the algorithm is that there should not be negative cycles (a cycle whose sum of edges produces a negative value) in the graph. Consider the following graph with cycle.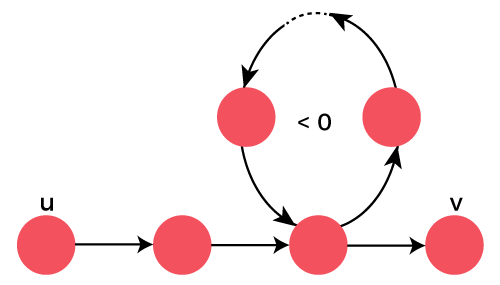

The runtime complexity of the algorithm is O(v*e) and space complexity is O(v). One should use the algorithm if the graph has negative edge weights. Therefore, the Bellman-Ford algorithm can be applied in the following situations:

Negative Edge Weights
Positive Edge Weights > 1
Undirected Cycles

The algorithm is slower than Dijkstra's algorithm when all arcs are negative.

Working of The Bellman-Ford Algorithm

The working of the Bellman-Ford algorithm is the same as Dijkstra's algorithm. The only difference is that it does not use the priority queue. It repetitively loops over all the edges and updates the distances at the start node, the same as in Dijkstra's algorithm.

If a graph G=(V, E) contains a negative weight cycle, then some shortest paths may not exist. Bellman-Ford algorithm finds all shortest path lengths from a source s ϵ V to all v ϵ V or determines that a negative weight cycle exists.

Given a weighted directed graph G(V, E) with source (s) and weight function w: E -> R, the algorithm returns a boolean value TRUE if and only if the graph contains no negative-weight cycles that are reachable from the source. The algorithm produces the shortest path and its weights. If there is such a cycle, the algorithm indicates that no solution exists.

Algorithm

INITIALIZE-SINGLE-SOURCE (G, s)
for i <- 1 to |V[G]|-1
do for each edge (U, V) ϵ E[G]
do RELEAX (U, V, W)
for each edge (U, V) ϵ E[G]
do if d[V] > d[U] + w (U, V)
then return FALSE
return TRUE

Bellman Ford Pseudo Code

BellamanFord (G, V, E, S)
Step 1:
for each vertex v ϵ G do
dist[v] = ∞
dist[source] = 0

Step 2:
Relax (u, v, w)
for i = 1 to |v|-1
           for each edge (u, v) ϵ G do
           (dist[v] > dist[u]+w(u, v))
           (dist[v] <- dist[u]+w(u, v))
Step 3:
for each edge (u, v) ϵ G
if (dist[u]+w(u, v)< dist[v])
return "Graph contains negative weight cycle"
return distance

Complexity

Time Complexity	Best Case	O(E)
	Average Case	O(VE)
	Worst Case	O(VE)
Space Complexity		O(V)

Let's understand the algorithm with an example.

Bellman-Ford Example

Consider the following directed graph (G).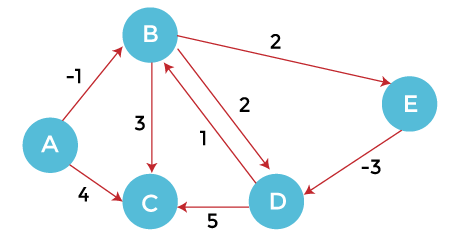

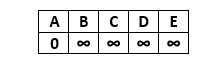
Order of edges: (B, E), (D, B), (B, D), (A, B), (A, C), (D, C), (B, C), (E, D)

In the above graph (G), A is the vertex node for all other vertexes.

In order to find the shortest path, first, we will initialize the source vertex (A) as 0 and other vertices with infinity (∞). After that, we will traverse towards each vertex from the source node. Update the value of the node during the traversal. We have created the following table for distance updation.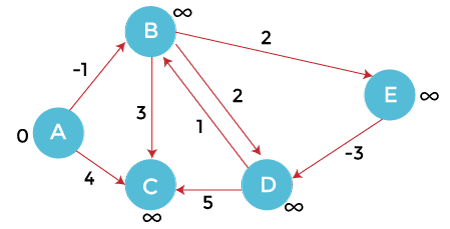

From the source vertex A, we can move to vertex B and C.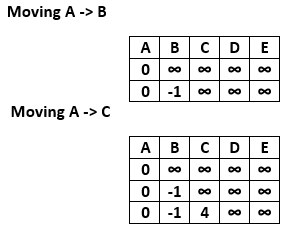

After updating the distances, we get the following graph.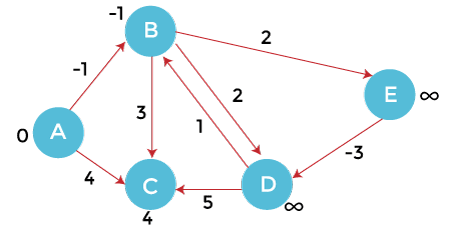

From vertex B, we can move to vertex C, D and E. Calculate the distance from B to other vertices, we get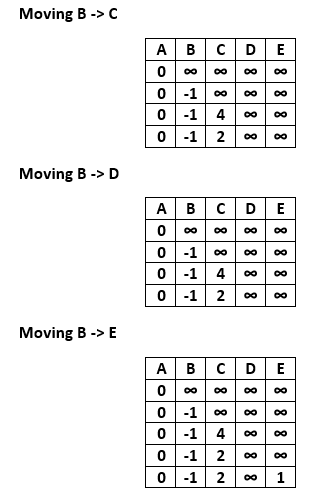

After updating the distances, we get the following graph.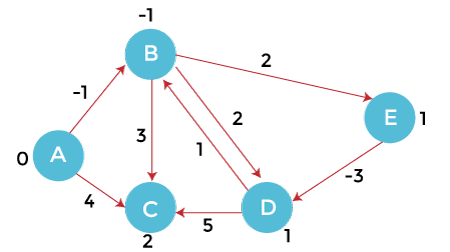

From vertex C we cannot move to any vertex, so we will visit the next vertex i.e. D.

From vertex D, we can move to vertex B and C. Calculate the distance from vertex D to other vertices.

Moving D -> B, we observe that the vertex B is already has the minimum distance, so we will not update the distance at this time.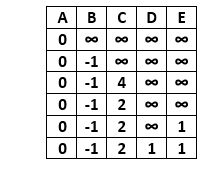

Moving D-> C, we observe that the vertex C already has the minimum distance, so we will not update the distance at this time.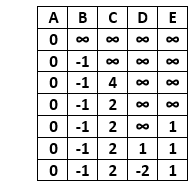

After updating the distances, we get the following graph.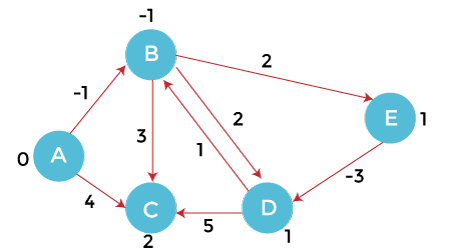

From vertex E, we can move to vertex D only. Calculate the distance from vertex E to D.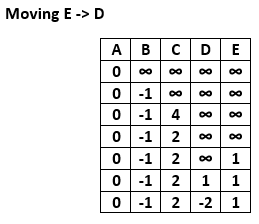

After updating the distances, we get the following graph.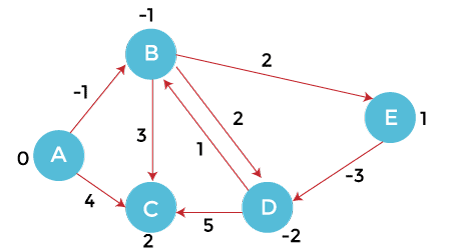

We observe that values decrease monotonically.

Bellman-Ford Implementation in Java

BellmanFordExample1.java

import 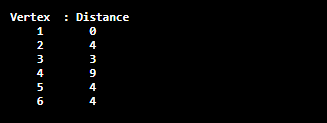java.util.ArrayList;
import java.util.List;
class Graph 
{
//vertices of the graph
private int V;  
//edges in the graph
private List<Edge> edges; 
//creating a constructor of the Graph class and generating getters and setters
public Graph(int v) 
{
V = v;
edges = new ArrayList<Edge>();
}
public int getV() 
{
return V;
}
public void setV(int v) 
{
V = v;
}
public List<Edge> getEdges() 
{
return edges;
}
public void setEdges(List<Edge> edges) 
{
this.edges = edges;
}
public void addEdge(int u, int v, int w) 
{
Edge e = new Edge(u, v, w);
edges.add(e);
}
}
class Edge 
{
//it is the source vertex    
private int u; 
//it is the destination vertex
private int v; 
//it denotes the weight on edge
private int w; 
//generating getters and setters
public int getU() 
{
return u;
}
public void setU(int u) 
{
this.u = u;
}
public int getV() 
{
return v;
}
public void setV(int v) 
{
this.v = v;
}
public int getW() 
{
return w;
}
public void setW(int w) 
{
this.w = w;
}
//creating constructor of the Edge class
public Edge(int u, int v, int w) 
{
this.u = u;
this.v = v;
this.w = w;
}
}
public class BellmanFordImplementation
{
public static void main(String args[]) 
{
Graph g = createGraph();
int distance[] = new int[g.getV()];
boolean hasNegativeCycle = getShortestPaths(g, 1, distance);
if(!hasNegativeCycle) 
{
System.out.println("Vertex \t: Distance");    
for(int i = 1; i < distance.length; i++)
System.out.println("\t"+i + " " + "\t\t"+(distance[i] == Integer.MAX_VALUE ? "-" : distance[i]));
} 
else 
{
System.out.println("Negative cycle exists in the graph, no solution found!!!");
}
}
private static Graph createGraph() 
{
int v = 7;
//creating a graph having 7 vertices
Graph g = new Graph(v);
//adding edges to the graph
g.addEdge(1, 2, 4);
g.addEdge(1, 4, 9);
g.addEdge(2, 3, -1);
g.addEdge(3, 6, 3);
g.addEdge(4, 3, 2);
g.addEdge(4, 5, -5);
g.addEdge(5, 6, 0);     
//returns graph
return g;
}
//Bellman-Ford logic
public static boolean getShortestPaths(Graph g, int source, int[] distance) 
{
int V = g.getV();
//initializing distances from source to other vertices
for(int i = 1; i < V; i++) 
{
distance[i] = Integer.MAX_VALUE;
}
//source vertex initialize to 0
distance[source] = 0;
//relaxing edges
for(int i = 1; i < V; i++) 
{
//iterate over edges    
for(Edge e: g.getEdges()) 
{
int u = e.getU(), v = e.getV(), w = e.getW();
if(distance[u] != Integer.MAX_VALUE && distance[v] > distance[u] + w) 
{
//calculates distance    
distance[v] = distance[u] + w;
}
}
}
//checks if there exist negative cycles in graph G
for(Edge e: g.getEdges()) 
{
int u = e.getU(), v = e.getV(), w = e.getW();
if(distance[u] != Integer.MAX_VALUE && distance[v] > distance[u] + w) 
{
return true;
}
}
return false;
}
}

Output:

Conclusion

Find the shortest path in a graph having non-negative edges weight is an NP-hard problem. For solving such problems, there is no polynomial-time algorithm exists. Consider a scenario, in which each edge has a negative edge weight, we can apply the Bellman-Ford algorithm.

There might be a negative-weight cycle that is reachable from the source. In such a case the algorithm will be terminated. In the same way, if we want to find the longest simple path from source (s) to vertex (v) and the graph has negative cycles, we cannot apply the Bellman-Ford algorithm.

Next TopicBigDecimal toString() in Java

← prev next →