Binary Tree Java

Binary tree is a tree type non-linear data structure that are mainly used for sorting and searching because they store data in hierarchical form. In this section, we will learn the implementation of binary tree data structure in Java. Also, provides a short description of binary tree data structure.

Binary Tree

A tree in which each node (parent) has at most two-child nodes (left and right) is called binary tree. The top most node is called the root node. In a binary tree a node contains the data and the pointer (address) of the left and right child node.

The height of a binary tree is the number of edges between the tree's root and its furthest (deepest) leaf. If the tree is empty, the height is 0. The height of the node is denoted by h.

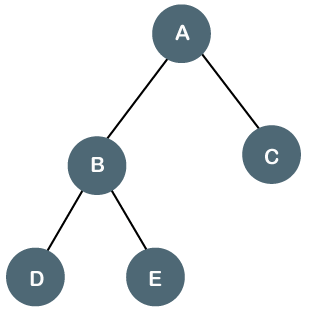
The height of the above binary tree is 2.

We can calculate the number of leaves and node by using the following formula.

Maximum number of leaf nodes is a binary tree: 2^h
Maximum number of nodes is a binary tree: 2^h+1-1

Where, h is the height of binary tree.

Example of Binary Tree

Types of Binary Tree

There are the following types of binary tree in data structure:

Full/ Strictly Binary Tree
Complete Binary Tree
Perfect Binary Tree
Balance Binary Tree
Rooted Binary Tree
Degenerated/ Pathological Binary Tree
Extended Binary Tree
Skewed Binary Tree
1. Left-skewed Binary Tree
2. Right-skewed Binary Tree
Threaded Binary Tree
1. Single Threaded Binary Tree
2. Double Threaded Binary Tree

Binary Tree Implementation in Java

There are many ways to implement binary tree. In this section, we will implement binary tree using LinkedList data structure. Along with it, we will also implement the traversal orders, searching a node and insert a node in a binary tree.

Implementation of Binary Tree Using LinkedList

Algorithm

Define Node class that contains three attributes namely: data left and right. Here, left represents the left child of the node and right represents the right child of the node.

When a node is created, data will pass to data attribute of the node and both left and right will be set to null.
Define another class that has an attribute root.
Root represents the root node of the tree and initialize it to null.

insert() will add a new node to the tree:
- It checks whether the root is null, which means the tree is empty. It will add the new node as root.
- Else, it will add root to the queue.
- The variable node represents the current node.
- First, it checks whether a node has a left and right child. If yes, it will add both nodes to queue.
- If the left child is not present, it will add the new node as the left child.
- If the left is present, then it will add the new node as the right child.
inorder() will display nodes of the tree in inorder fashion.
- It traverses the entire tree then prints out left child followed by root then followed by the right child.

BinarySearchTree.java

public class BinarySearchTree {  
    //Represent the node of binary tree  
    public static class Node{  
        int data;  
        Node left;  
        Node right;  
        public Node(int data){  
            //Assign data to the new node, set left and right children to null  
            this.data = data;  
            this.left = null;  
            this.right = null;  
            }  
        }  
    //Represent the root of binary tree  
    public Node root;  
    public BinarySearchTree(){  
        root = null;  
    }  
    //factorial() will calculate the factorial of given number  
    public int factorial(int num) {  
        int fact = 1;  
        if(num == 0)  
            return 1;  
        else {  
            while(num > 1) {  
                fact = fact * num;  
                num--;  
            }  
            return fact;  
        }  
    }  
    //numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key  
    public int numOfBST(int key) {  
        int catalanNumber = factorial(2 * key)/(factorial(key + 1) * factorial(key));  
        return catalanNumber;  
    }  
    public static void main(String[] args) {  
        BinarySearchTree bt = new BinarySearchTree();  
        //Display total number of possible binary search tree with key 5  
        System.out.println("Total number of possible Binary Search Trees with given key: " + bt.numOfBST(5));  
      }  
}  

Output:

Binary tree after insertion
1 
Binary tree after insertion
2 1 3 
Binary tree after insertion
4 2 5 1 3 
Binary tree after insertion
4 2 5 1 6 3 7

Binary Tree Operations

The following operations can be performed on a binary tree:

Insertion
Deletion
Search
Traversal

Java Program to Insert a Node in Binary Tree

BinaryTreeInsert.java

public class BinaryTreeInsert 
{
    public static void main(String[] args) 
    {
        new BinaryTreeInsert().run();
    }
    static class Node 
    {
        Node left;
        Node right;
        int value;
        public Node(int value) 
        {
            this.value = value;
        }
    }
    public void run() 
    {
        Node rootnode = new Node(25);
        System.out.println("Building tree with root value " + rootnode.value);
        System.out.println("=================================");
        insert(rootnode, 11);
        insert(rootnode, 15);
        insert(rootnode, 16);
        insert(rootnode, 23);
        insert(rootnode, 79);
    }
    public void insert(Node node, int value) 
    {
        if (value < node.value) 
        {
            if (node.left != null) 
            {
                insert(node.left, value);
            } else 
            {
                System.out.println("  Inserted " + value + " to left of Node " + node.value);
                node.left = new Node(value);
            }
        } 
        else if (value > node.value) 
        {
            if (node.right != null) 
            {
                insert(node.right, value);
            } else 
            {
                System.out.println("  Inserted " + value + " to right of Node " + node.value);
                node.right = new Node(value);
            }
        }
    }
}

Output:

Building tree with root value 25
=================================
  Inserted 11 to left of Node 25
  Inserted 15 to right of Node 11
  Inserted 16 to right of Node 15
  Inserted 23 to right of Node 16
  Inserted 79 to right of Node 25

Java Program to Delete a Node in Java

Algorithm

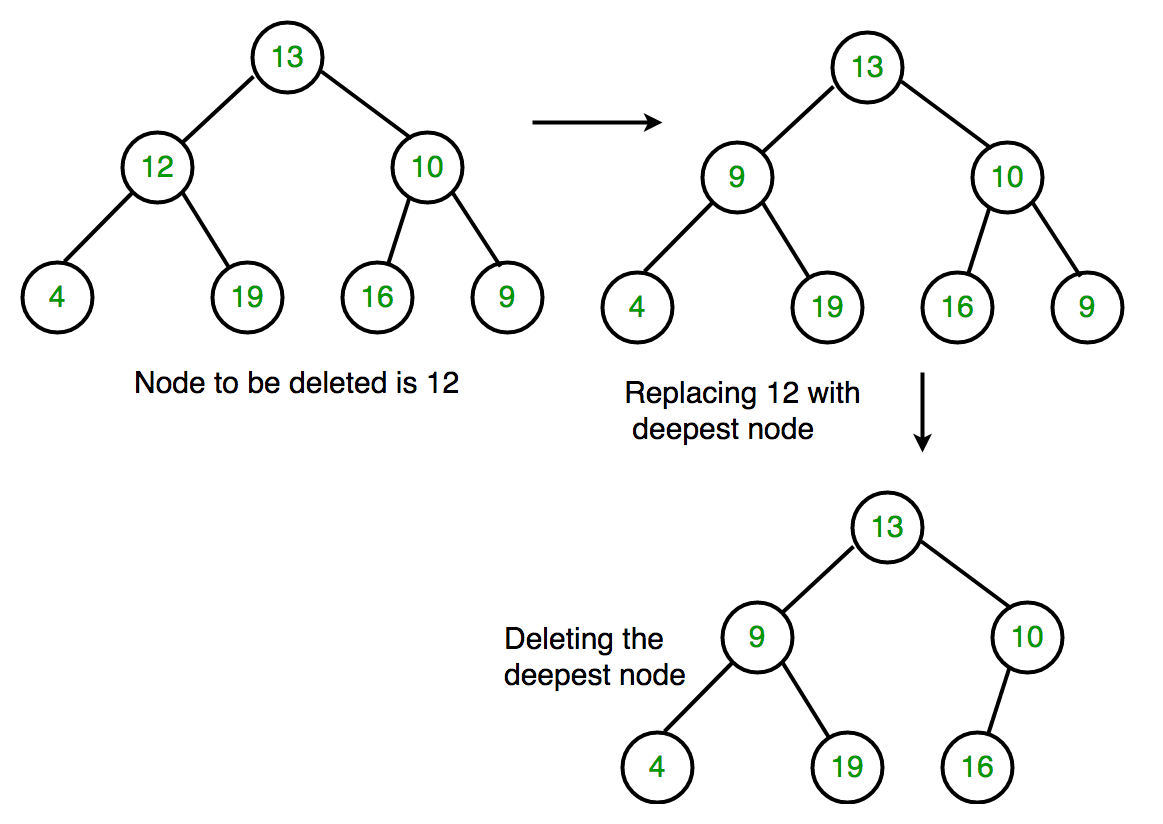
Starting at the root, find the deepest and rightmost node in binary tree and node that we want to delete.
Replace the deepest rightmost node's data with the node to be deleted.
Then delete the deepest rightmost node.

Consider the following figure.

DeleteNode.java

import java.util.LinkedList;
import java.util.Queue;
public class DeleteNode 
{
// A binary tree node has key, pointer to
// left child and a pointer to right child
static class Node
{
	int key;
	Node left, right;
	
	// Constructor
	Node(int key)
	{
		this.key = key;
		left = null;
		right = null;
	}
}
static Node root;
static Node temp = root;
// Inorder traversal of a binary tree
static void inorder(Node temp)
{
	if (temp == null)
		return;
	inorder(temp.left);
	System.out.print(temp.key + " ");
	inorder(temp.right);
}
// Function to delete deepest
// element in binary tree
static void deleteDeepest(Node root, Node delNode)
{
	Queue<Node> q = new LinkedList<Node>();
	q.add(root);
	Node temp = null;
	// Do level order traversal until last node
	while (!q.isEmpty())
	{
		temp = q.peek();
		q.remove();
		
		if (temp == delNode)
		{
			temp = null;
			return;
		}
		if (temp.right!=null)
		{
			if (temp.right == delNode)
			{
				temp.right = null;
				return;
		}
		else
			q.add(temp.right);
	}
	if (temp.left != null)
	{
		if (temp.left == delNode)
		{
			temp.left = null;
			return;
		}
		else
			q.add(temp.left);
	}
}
}
// Function to delete given element
// in binary tree
static void delete(Node root, int key)
{
	if (root == null)
		return;
		
	if (root.left == null &&
	root.right == null)
	{
		if (root.key == key)
		{
			root=null;
			return;
		}
		else
			return;
	}
	Queue<Node> q = new LinkedList<Node>();
	q.add(root);
	Node temp = null, keyNode = null;
	// Do level order traversal until
	// we find key and last node.
	while (!q.isEmpty())
	{
		temp = q.peek();
		q.remove();
		if (temp.key == key)
			keyNode = temp;
		if (temp.left != null)
			q.add(temp.left);
		if (temp.right != null)
			q.add(temp.right);
	}
	if (keyNode != null)
	{
		int x = temp.key;
		deleteDeepest(root, temp);
		keyNode.key = x;
	}
}
// Driver code
public static void main(String args[])
{
	root = new Node(10);
	root.left = new Node(11);
	root.left.left = new Node(7);
	root.left.right = new Node(12);
	root.right = new Node(9);
	root.right.left = new Node(15);
	root.right.right = new Node(8);
	System.out.print("Inorder traversal before deletion: ");
	inorder(root);
	//node to delete
	int key = 7;
	delete(root, key);
	System.out.print("\nInorder traversal after deletion: ");
	inorder(root);
}
}

Output:

Inorder traversal before deletion: 7 11 12 10 15 9 8 
Inorder traversal after deletion: 8 11 12 10 15 9

Java Program to Search a Node in Binary Tree

Algorithm

Define Node class which has three attributes namely: data left and right. Here, left represents the left child of the node and right represents the right child of the node.
When a node is created, data will pass to data attribute of the node and both left and right will be set to null.
Define another class which has two attribute root and flag.
1. Root represents the root node of the tree and initializes it to null.
2. The Flag will be used to check whether the given node is present in the tree or not. Initially, it will be set to false.

searchNode() will search for a particular node in the binary tree:
- It checks whether the root is null, which means the tree is empty.
- If the tree is not empty, it will compare temp's data with value. If they are equal, it will set the flag to true and return.
- Traverse left subtree by calling searchNode() recursively and check whether the value is present in left subtree.
- Traverse right subtree by calling searchNode() recursively and check whether the value is present in the right subtree.

SearchBinaryTree.java

public class SearchBinaryTree 
{  
      //Represent a node of binary tree  
      public static class Node
{  
        int data;  
        Node left;  
        Node right;  
        public Node(int data)
        {  
          //Assign data to the new node, set left and right children to null  
          this.data = data;  
          this.left = null;  
          this.right = null;  
        }  
      }  
      //Represent the root of binary tree  
      public Node root;  
      public static boolean flag = false;  
      public SearchBinaryTree()
      {  
        root = null;  
      }  
      //searchNode() will search for the particular node in the binary tree  
      public void searchNode(Node temp, int value)
      {  
        //Check whether tree is empty  
        if(root == null)
        {  
          System.out.println("Tree is empty");  
        }  
        else
        {  
          //If value is found in the given binary tree then, set the flag to true  
          if(temp.data == value)
          {  
            flag = true;  
               return;  
          }  
          //Search in left subtree  
          if(flag == false && temp.left != null)
          {  
          searchNode(temp.left, value);  
          }  
          //Search in right subtree  
          if(flag == false && temp.right != null)
          {  
          searchNode(temp.right, value);  
          }  
        }  
      }  
      public static void main(String[] args) 
      {  
        SearchBinaryTree bt = new SearchBinaryTree();  
        //Add nodes to the binary tree  
        bt.root = new Node(11);  
        bt.root.left = new Node(8);  
        bt.root.right = new Node(12);  
        bt.root.left.left = new Node(78);  
        bt.root.right.left = new Node(23);  
        bt.root.right.right = new Node(36);  
        //Search for node 5 in the binary tree  
           bt.searchNode(bt.root, 23);  
        if(flag)  
          System.out.println("Element is present in the binary tree.");  
        else  
          System.out.println("Element is not present in the binary tree.");  
      }  
    }  

Output:

Element is present in the binary tree.

Binary Tree Traversal

Traversal Order	First Visit	Second Visit	Third Visit
Inorder	Visit left subtree in inorder	Visit root node	Visit right subtree in inorder
Preorder	Visit root node	Visit left subtree in preorder	Visit right subtree in preorder
Postorder	Visit left subtree in postorder	Visit right subtree in postorder	Visit root node

Note: Except the above three traversals, there is another traversal order is called boundary traversal.

Java Program to Traverse Inorder, Preorder, and Postorder Traversal

BinaryTree.java

public class BinaryTree 
{
  // first node
  private Node root;
  BinaryTree()
  {
    root = null;
  }
  // Class representing tree nodes
  static class Node
  {
    int value;
    Node left;
    Node right;
    Node(int value)
    {
      this.value = value;
      left = null;
      right = null;        
    }
    public void displayData()
    {
      System.out.print(value + " ");
    }
  }
    
  public void insert(int i)
  {
    root = insert(root, i);
  }
  //Inserting node - recursive method
  public Node insert(Node node, int value)
  {
    if(node == null){
      return new Node(value);
    }
    // Move to the left if passed value is 
    // less than the current node
    if(value < node.value)
    {
      node.left = insert(node.left, value);
    }
    // Move to the right if passed value is 
    // greater than the current node
    else if(value > node.value)
    {
      node.right = insert(node.right, value);
    }
    return node;
  }
  // Search node in binary search tree
  public Node find(int searchedValue)
  {
    Node current = root;
    while(current.value != searchedValue)
    {
      if(searchedValue < current.value)
        // Move to the left if searched value is less
        current = current.left;
      else
        // Move to the right if searched value is >=
        current = current.right;
      if(current == null)
      {
        return null;
      }
    }
    return current;
  }
  // For traversing in order
  public void inOrder(Node node)
  {
    if(node != null)
    {
      inOrder(node.left);
      node.displayData();
      inOrder(node.right);
    }
  }
  // Preorder traversal
  public void preOrder(Node node)
  {
    if(node != null){
      node.displayData();
      preOrder(node.left);           
      preOrder(node.right);
    }
  }
  // Postorder traversal
  public void postOrder(Node node)
  {
    if(node != null)
    {
      postOrder(node.left);
      postOrder(node.right);
      node.displayData();          
    }
  }
  public static void main(String[] args) 
  {
    BinaryTree bst = new BinaryTree();
    bst.insert(34);
    bst.insert(56);
    bst.insert(12);
    bst.insert(89);
    bst.insert(67);
    bst.insert(90);
    System.out.println("Inorder traversal of binary tree");
    bst.inOrder(bst.root);
    System.out.println();
    System.out.println("Preorder traversal of binary tree");
    bst.preOrder(bst.root);
    System.out.println();
    System.out.println("Postorder traversal of binary tree");
    bst.postOrder(bst.root);
    System.out.println();
  }
}

Output:

Inorder traversal of binary tree
12 34 56 67 89 90 
Preorder traversal of binary tree
34 12 56 89 67 90 
Postorder traversal of binary tree
12 67 90 89 56 34

Besides the above operations, we can also perform the operations such as large node, smallest node, and sum of all nodes.

Java Program to Find the Largest Node in Binary Tree

LargestNode.java

public class LargestNode 
{  
    //Represent the node of binary tree  
    public static class Node
    {  
        int data;  
        Node left;  
        Node right;  
        public Node(int data)
        {  
            //Assign data to the new node, set left and right children to null  
            this.data = data;  
            this.left = null;  
            this.right = null;  
        }  
     }  
      //Represent the root of binary tree  
      public Node root;  
      public LargestNode()
      {  
        root = null;  
      }  
      //largestElement() will find out the largest node in the binary tree  
      public int largestElement(Node temp)
      {  
          //Check whether tree is empty  
           if(root == null) 
           {  
               System.out.println("Tree is empty");  
               return 0;  
            }  
           else
           {  
               int leftMax, rightMax;  
               //Max will store temp's data  
               int max = temp.data;  
               //It will find largest element in left subtree  
               if(temp.left != null){  
                   leftMax = largestElement(temp.left);  
                   //Compare max with leftMax and store greater value into max  
                   max = Math.max(max, leftMax);  
                }  
                //It will find largest element in right subtree  
                if(temp.right != null){  
                    rightMax = largestElement(temp.right);  
                    //Compare max with rightMax and store greater value into max  
                    max = Math.max(max, rightMax);  
                }  
                return max;  
           }  
      }  
      public static void main(String[] args) 
      {  
        LargestNode bt = new LargestNode();  
        //Add nodes to the binary tree  
        bt.root = new Node(90);  
        bt.root.left = new Node(99);  
        bt.root.right = new Node(23);  
        bt.root.left.left = new Node(96);  
        bt.root.right.left = new Node(45);  
        bt.root.right.right = new Node(6);  
         bt.root.right.left = new Node(13);  
         bt.root.right.right = new Node(77);  
        //Display largest node in the binary tree  
        System.out.println("Largest element in the binary tree: " + bt.largestElement(bt.root));  
      }  
}  

Output:

Largest element in the binary tree: 99

Java Program to Find the Smallest Node in Binary Tree

Algorithm

Define Node class which has three attributes namely: data, left and right. Here, left represents the left child of the node and right represents the right child of the node.
When a node is created, data will pass to data attribute of node and both left and right will be set to null.
Define another class which has an attribute root.
1. Rootrepresent root node of the tree and initialize it to null.

smallestElement() will find out the smallest node in binary tree:
1. It checks whether root is null, which means tree is empty.
2. If tree is not empty, define a variable min that will store temp's data.
3. Find out the minimum node in left subtree by calling smallestElement() recursively. Store that value in leftMin. Compare the value of min with leftMin and store the minimum of two to min.
4. Find out the minimum node in right subtree by calling smallestElement() recursively. Store that value in rightMin. Compare the value of min with rightMin and store the maximum of two to min.
5. At the end, min will hold the smallest node in the binary tree.

SmallestNode.java

public class SmallestNode 
{  
      //Represent the node of binary tree  
      public static class Node
      {  
        int data;  
        Node left;  
        Node right;  
        public Node(int data)
        {  
            //Assign data to the new node, set left and right children to null  
            this.data = data;  
            this.left = null;  
            this.right = null;  
        }  
      }  
      //Represent the root of binary tree  
      public Node root;  
      public SmallestNode()
      {  
          root = null;  
      }  
      //smallestElement() will find out the smallest node in the binary tree  
      public int smallestElement(Node temp)
      {  
          //Check whether tree is empty  
          if(root == null) 
          {  
              System.out.println("Tree is empty");  
              return 0;  
          }  
          else 
          {  
                int leftMin, rightMin;  
                //Min will store temp's data  
                int min = temp.data;  
                //It will find smallest element in left subtree  
                if(temp.left != null)
                {  
                  leftMin = smallestElement(temp.left);  
                  //If min is greater than leftMin then store the value of leftMin into min  
                  min = Math.min(min, leftMin);  
                }  
                //It will find smallest element in right subtree  
                if(temp.right != null)
                {  
                  rightMin = smallestElement(temp.right);  
                  //If min is greater than rightMin then store the value of rightMin into min  
                  min = Math.min(min, rightMin);  
                }  
                return min;  
          }  
      }  
      public static void main(String[] args) {  
        SmallestNode bt = new SmallestNode();  
        //Add nodes to the binary tree  
        bt.root = new Node(9);  
        bt.root.left = new Node(5);  
        bt.root.right = new Node(7);  
        bt.root.left.left = new Node(1);  
        bt.root.right.left = new Node(2);  
        bt.root.right.right = new Node(8);  
        bt.root.right.left = new Node(4);  
        bt.root.right.right = new Node(3);  
        //Display smallest node in the binary tree  
        System.out.println("Smallest element in the binary tree: " + bt.smallestElement(bt.root));  
      }  
}  

Output:

Smallest element in the binary tree: 1

Java Program to Find the Maximum Width of a Binary Tree

Algorithm

Define Node class which has three attributes namely: data left and right. Here, left represents the left child of the node and right represents the right child of the node.
When a node is created, data will pass to data attribute of the node and both left and right will be set to null.
Define another class which has an attribute root.
1. Root represents the root node of the tree and initializes it to null.
findMaximumWidth() will find out the maximum width of the given binary tree:
1. Variable maxWidth will store the maximum number of nodes present in any level.
2. The queue is used for traversing binary tree level-wise.
3. It checks whether the root is null, which means the tree is empty.
4. If not, add the root node to queue. Variable nodesInLevel keeps track of the number of nodes in each level.
5. If nodesInLevel > 0, remove the node from the front of the queue and add its left and right child to the queue. For the first iteration, node 1 will be removed and its children nodes 2 and 3 will be added to the queue. In the second iteration, node 2 will be removed, its children 4 and 5 will be added to the queue and so on.
6. MaxWidth will store max(maxWidth, nodesInLevel). So, at any given point of time, it will represent the maximum number of nodes.
7. This will continue till all the levels of the tree is traversed.

BinaryTree.java

import java.util.LinkedList;  
import java.util.Queue;  
   
public class BinaryTree 
{  
    //Represent the node of binary tree  
      public static class Node
      {  
        int data;  
        Node left;  
        Node right;  
        public Node(int data)
        {  
          //Assign data to the new node, set left and right children to null  
          this.data = data;  
          this.left = null;  
          this.right = null;  
        }  
      }  
      //Represent the root of binary tree  
      public Node root; 
      public BinaryTree()
      {  
        root = null;  
      }  
//findMaximumWidth() will find out the maximum width of the given binary tree  
      public int findMaximumWidth() 
      {  
          int maxWidth = 0;  
          //Variable nodesInLevel keep tracks of number of nodes in each level  
          int nodesInLevel = 0;  
          //queue will be used to keep track of nodes of tree level-wise  
          Queue<Node> queue = new LinkedList<Node>();  
          //Check if root is null, then width will be 0  
          if(root == null) {  
              System.out.println("Tree is empty");  
              return 0;  
          }  
          else 
          {  
              //Add root node to queue as it represents the first level  
              queue.add(root); 
              while(queue.size() != 0) 
              {  
                  //Variable nodesInLevel will hold the size of queue i.e. number of elements in queue  
                  nodesInLevel = queue.size();  
                  //maxWidth will hold maximum width.   
                  //If nodesInLevel is greater than maxWidth then, maxWidth will hold the value of nodesInLevel  
                  maxWidth = Math.max(maxWidth, nodesInLevel);  
                  //If variable nodesInLevel contains more than one node   
                  //then, for each node, we'll add left and right child of the node to the queue  
                  while(nodesInLevel > 0) 
                  {  
                     Node current = queue.remove();  
                     if(current.left != null)   
                         queue.add(current.left);  
                     if(current.right != null)   
                         queue.add(current.right);  
                     nodesInLevel--;  
                  }  
              }  
          }  
          return maxWidth;  
      }  
      public static void main(String[] args) 
      {  
          BinaryTree bt = new BinaryTree();  
          //Add nodes to the binary tree  
          bt.root = new Node(1);  
          bt.root.left = new Node(2);  
          bt.root.right = new Node(3);  
          bt.root.left.left = new Node(4);  
          bt.root.left.right = new Node(5);  
          bt.root.right.left = new Node(6);  
          bt.root.right.right = new Node(7);  
          bt.root.left.left.left = new Node(8);  
          //Display the maximum width of given tree  
          System.out.println("Maximum width of the binary tree: " + bt.findMaximumWidth());  
      }  
}  

Output: