Branching Statements in Java

Branching statements are used to change the flow of execution from one section of a program to another. Branching statements are typically utilized within control statements. Java includes three types of branching statements: continue, break, and return. When a given condition is met, we can depart from a control statement using branching statements.

In Java, the continue and break statements are two key branching statements that are used in conjunction with the control statements. The break statement ends or breaks the loop and moves control outside of it. The continue command skips the current execution and returns control to the loop's beginning. The return statement returns a value from a method and does so openly.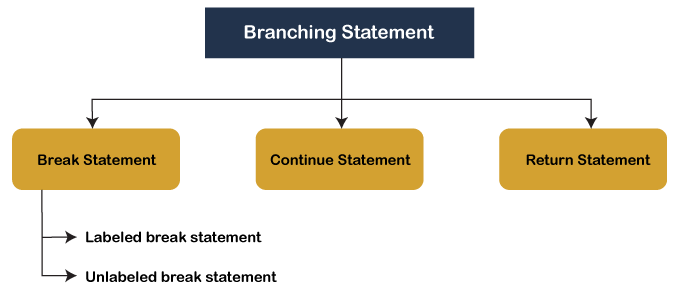

The break Statement

The break statement is used to abruptly exit a loop or switch statement.

In a for, while, or do-while loop: It ends the loop's execution instantly, enabling the program to proceed with the code after the loop.

In a switch statement, it quits the switch block, preventing further case blocks from being executed.

Syntax

while (true) {
    // Code here
    if (condition) {
        break; // Exit the loop
    }
}

Example1:

BranchingStatements.java

public class BranchingStatements {
    public static void main(String[] args) {
        int[] numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
        for (int num : numbers) {
            if (num == 5) {
                break; // Exit the loop when num is 5
            }
            System.out.println(num);
        }
    }
}

Output:

Example2:

BranchingStatements.java

public class BranchingStatements {
    public static void main(String[] args) {
        int[] numbers = {10, 20, 30, 40, 50};
        int target = 30;
        boolean found = false;
        for (int num : numbers) {
            if (num == target) {
                found = true;
                break; // Exit the loop when the target element is found
            }
        }
        if (found) {
            System.out.println("Element found!");
        } else {
            System.out.println("Element not found.");
        }
    }
}

Output:

Element found!

Explanation

This program in Java searches an array of integers for a specified target element. It sets a boolean variable discovered to false to indicate whether or not the target element was found. It then uses a for-each loop to run through each element of the array. If it finds an element that matches the target, it sets found to true and exits the loop early using the break statement. Following the loop, it examines the value of found to see if the target element was discovered. It prints "Element found!" if found is true; else, it publishes "Element not found." This software stops searching as soon as it finds the target element, which improves speed for huge arrays.

The continue Statement

The continue statement is used to skip the current loop iteration and go to the next.

It is commonly used within loops such as for, while, or do-while.

When this happens, it skips the remaining code in the current iteration and moves on to the next.

Syntax

control-flow-statement;      
continue;  

for (int i = 0; condition; increment) {
    if (condition) {
        continue; // Skip this iteration and go to the next one
    }
    // Code here
}

Example1:

BranchingStatements.java

public class BranchingStatements {
    public static void main(String[] args) {
        for (int i = 1; i <= 10; i++) {
            if (i % 2 == 0) {
                continue; // Skip even numbers
            }
            System.out.println(i);
        }
    }
}

Output:

Example2:

BranchingStatements.java

public class BranchingStatements {
    public static void main(String[] args) {
        int[] data = {5, -2, 10, -8, 15};
        int sum = 0;
        for (int num : data) {
            if (num < 0) {
                continue; // Skip negative numbers
            }
            sum += num;
        }
        System.out.println("Sum of positive numbers: " + sum);
    }
}

Output:

Sum of positive numbers: 30

Explanation

A data array holding integers is defined in the corresponding Java application. The program then sets the variable sum to zero. Using a for-each loop, it iterates through each member of the data array. It verifies whether the current element is less than zero throughout each iteration. If num is negative, the continue statement is executed, which skips the remaining code in that iteration and moves on to the next array element. This essentially bypasses the handling of negative values. It adds the value of num to the sum variable for positive values, aggregating the sum of positive numbers. Finally, the program displays the total of the positive numbers as "Sum of positive numbers: [sum]."

The return Statement

The return statement is used to quit a method and, if desired, return a value to the caller.

It defines the value that the method should return (if the method has a return type).

It also causes the function to quit instantly, bypassing any code that comes after the method's return statement.

Syntax

return value;  

public int add(int a, int b) {
    return a + b; // Return the result and exit the method
}

Example1:

BranchingStatements.java

public class BranchingStatements {
    public static void main(String[] args) {
        int result = add(5, 3);
        System.out.println("The sum is: " + result);
    }
    public static int add(int a, int b) {
        int sum = a + b;
        return sum; // Return the result to the caller
    }
}

Output:

The sum is: 8

Example2:

BranchingStatements2.java

public class BranchingStatements2 {
    public static void main(String[] args) {
        int n = 5;
        long factorial = calculateFactorial(n);
        System.out.println("Factorial of " + n + " is " + factorial);
    }
    public static long calculateFactorial(int n) {
        if (n == 0 || n == 1) {
            return 1; // Base case: factorial of 0 and 1 is 1
        } else {
            return n * calculateFactorial(n - 1); // Recursive call
        }
    }
}

Output:

Factorial of 5 is 120

Explanation

The Java program "Main" computes the factorial of a given number "n" using a recursive function. The calculateFactorial() function looks for a base case in which if "n" is 0 or 1, it returns 1 because the factorial of these integers is specified as 1. For other values of "n," a recursive call is made to determine the factorial by multiplying "n" by the factorial of "n-1." In the "main" technique, this computation is demonstrated by calculating the factorial of 5 and reporting the answer, which is "Factorial of 5 is 120." Recursive functions are well-suited for issues involving recurring subtasks, and it efficiently calculates the factorial in this example.

Next TopicCircuit Breaker Pattern Java

← prev next →