Dijkstra Algorithm Java

Dijkstra algorithm is one of the prominent algorithms to find the shortest path from the source node to a destination node. It uses the greedy approach to find the shortest path. The concept of the Dijkstra algorithm is to find the shortest distance (path) starting from the source point and to ignore the longer distances while doing an update.

In this section, we will implement the Dijkstra algorithm in Java program. Also, we will discuss its usage and limitations.

Dijkstra Algorithm Steps

Step1: All nodes should be marked as unvisited.

Step2: All the nodes must be initialized with the "infinite" (a big number) distance. The starting node must be initialized with zero.

Step3: Mark starting node as the current node.

Step4: From the current node, analyze all of its neighbors that are not visited yet, and compute their distances by adding the weight of the edge, which establishes the connection between the current node and neighbor node to the current distance of the current node.

Step5: Now, compare the recently computed distance with the distance allotted to the neighboring node, and treat it as the current distance of the neighboring node,

Step6: After that, the surrounding neighbors of the current node, which has not been visited, are considered, and the current nodes are marked as visited.

Step7: When the ending node is marked as visited, then the algorithm has done its job; otherwise,

Step8: Pick the unvisited node which has been allotted the minimum distance and treat it as the new current node. After that, start again from step4.

Dijkstra Algorithm Pseudo Code

Method Dijkstra(G, s): // G is graph, s is source
distance[s] -> 0               // Distance from the source to source is always 0
for every vertex vx in the Graph G: // doing the initialization work
{
if vx ? s
{
// Unknown distance function from source to each node set to infinity
distance[vx] -> infinity 
}
add vx to Queue Q   // Initially, all the nodes are in Q
}

// The while loop
Untill the Q is not empty:                  
{
// During the first run, this vertex is the source or starting node
vx = vertex in Q with the minimum distance[vx] 
delete vx from Q 
}
// where the neighbor ux has not been deleted yet from Q.
for each neighbor ux of vx:           
              alt = distance[vx] + length(vx, ux)
              // A path with lesser weight (shorter path), to ux is found
              if alt < distance[ux]:               
                  distance[ux] = alt            // updating the distance of ux 

      return dist[]
  end Method

Implementation of Dijkstra Algorithm

The following code implements the Dijkstra Algorithm using the diagram mentioned below.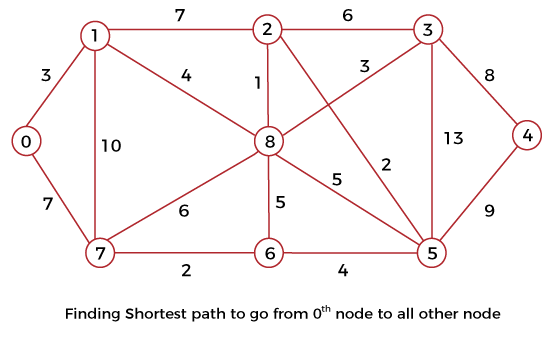

FileName: DijkstraExample.java

// A Java program that finds the shortest path using Dijkstra's algorithm.
// The program uses the adjacency matrix for the representation of a graph 

// import statements
import java.util.*;
import java.io.*;
import java.lang.*;

public class DijkstraExample 
{
// A utility method to compute the vertex with the distance value, which is minimum
// from the group of vertices that has not been included yet 
static final int totalVertex = 9;
int minimumDistance(int distance[], Boolean spSet[])
{
// Initialize min value
int m = Integer.MAX_VALUE, m_index = -1;

for (int vx = 0; vx < totalVertex; vx++)
{
if (spSet[vx] == false && distance[vx] <= m) 
{
m = distance[vx];
m_index = vx;
}
}
return m_index;

}

// A utility method to display the built distance array
void printSolution(int distance[], int n)
{
System.out.println("The shortest Distance from source 0th node to all other nodes are: ");
for (int j = 0; j < n; j++)
System.out.println("To " + j + " the shortest distance is: " + distance[j]);
}

// method that does the implementation of Dijkstra's shortest path algorithm
// for a graph that is being represented using the adjacency matrix representation
void dijkstra(int graph[][], int s)
{
int distance[] = new int[totalVertex]; // The output array distance[i] holds the shortest distance from source s to j

// spSet[j] will be true if vertex j is included in the shortest
// path tree or the shortest distance from the source s to j is finalized
Boolean spSet[] = new Boolean[totalVertex];

// Initializing all of the distances as INFINITE 
// and spSet[] as false
for (int j = 0; j < totalVertex; j++) 
{
distance[j] = Integer.MAX_VALUE;
spSet[j] = false;
}

// Distance from the source vertex to itself is always 0
distance[s] = 0;

// compute the shortest path for all the given vertices
for (int cnt = 0; cnt < totalVertex - 1; cnt++) 
{
// choose the minimum distance vertex from the set of vertices
// not yet processed. ux is always equal to source s in the first
// iteration.
int ux = minimumDistance(distance, spSet);

// the choosed vertex is marked as true
// it means it is processed
spSet[ux] = true;

// Updating the distance value of the neighboring vertices 
// of the choosed vertex.
for (int vx = 0; vx < totalVertex; vx++)

// Update distance[vx] if and only if it is not in the spSet, there is an
// edge from ux to vx, and the total weight of path from source s to
// vx through ux is lesser than the current value of distance[vx]
if (!spSet[vx] && graph[ux][vx] != -1 && distance[ux] != Integer.MAX_VALUE && distance[ux] + graph[ux][vx] < distance[vx])
{
distance[vx] = distance[ux] + graph[ux][vx];
}
}

// display the build distance array
printSolution(distance, totalVertex);
}

// main method
public static void main(String argvs[])
{
// A 9 * 9 matrix is created. 
// arr[x][y] = - 1 means, there is no any edge that connects the nodes x and y directly
int grph[][] = new int[][] { { -1, 3, -1, -1, -1, -1, -1, 7, -1 },
	{ 3, -1, 7, -1, -1, -1, -1, 10, 4 },
	{ -1, 7, -1, 6, -1, 2, -1, -1, 1 },
	{ -1, -1, 6, -1, 8, 13, -1, -1, 3 },
	{ -1, -1, -1, 8, -1, 9, -1, -1, -1 },
	{ -1, -1, 2, 13, 9, -1, 4, -1, 5 },
	{ -1, -1, -1, -1, -1, 4, -1, 2, 5 },
	{ 7, 10, -1, -1, -1, -1, 2, -1, 6 },
	{ -1, 4, 1, 3, -1, 5, 5, 6, -1 } };
	
// creating an object of the class DijkstraExample
DijkstraExample obj = new DijkstraExample();
obj.dijkstra(grph, 0);
}
}

Output:

The shortest Distance from source 0th node to all other nodes are: 
To 0 the shortest distance is: 0
To 1 the shortest distance is: 3
To 2 the shortest distance is: 8
To 3 the shortest distance is: 10
To 4 the shortest distance is: 18
To 5 the shortest distance is: 10
To 6 the shortest distance is: 9
To 7 the shortest distance is: 7
To 8 the shortest distance is: 7

The time complexity of the above code is O(V²), where V is the total number of vertices present in the graph. Such time complexity does not bother much when the graph is smaller but troubles a lot when the graph is of larger size. Therefore, we have to do the optimization to reduce this complexity. With the help of the priority queue, we can decrease the time complexity. Observe the following code that is written for the graph depicted above.

FileName: DijkstraExample1.java

// Java Program shows the implementation Dijkstra's Algorithm
// Using the Priority Queue

// import statement
import java.util.*;

// Main class DijkstraExample1
public class DijkstraExample1
{

// Member variables of the class
private int distance[];
private Set<Integer> settld;
private PriorityQueue<Node> pQue;

// Total count of the vertices
private int totalNodes;
List<List<Node> > adjacent;

// Constructor of the class
public DijkstraExample1(int totalNodes)
{

this.totalNodes = totalNodes;
distance = new int[totalNodes];
settld = new HashSet<Integer>();
pQue = new PriorityQueue<Node>(totalNodes, new Node());
}

public void dijkstra(List<List<Node> > adjacent, int s)
{
this.adjacent = adjacent;

for (int j = 0; j < totalNodes; j++)
{
// initializing the distance of every node to infinity (a large number)
distance[j] = Integer.MAX_VALUE;
}

// Adding the source node to pQue
pQue.add(new Node(s, 0));

// distance of the source is always zero
distance[s] = 0;

while (settld.size() != totalNodes) 
{

// Terminating condition check when
// the priority queue contains zero elements, return
if (pQue.isEmpty())
{
return;
}

// Deleting the node that has the minimum distance from the priority queue
int ux = pQue.remove().n;

// Adding the node whose distance is 
// confirmed
if (settld.contains(ux))
{
continue;
}

// We don't have to call eNeighbors(ux)
// if ux is already present in the settled set.
settld.add(ux);

eNeighbours(ux);
}
}

private void eNeighbours(int ux)
{

int edgeDist = -1;
int newDist = -1;

// All of the neighbors of vx
for (int j = 0; j < adjacent.get(ux).size(); j++) 
{
Node vx = adjacent.get(ux).get(j);

// If the current node hasn't been already processed
if (!settld.contains(vx.n)) 
{
    edgeDist = vx.price;
    newDist = distance[ux] + edgeDist;

    // If the new distance is lesser in the cost
    if (newDist < distance[vx.n])
    {
        distance[vx.n] = newDist;
    }

    // Adding the current node to the priority queue pQue
    pQue.add(new Node(vx.n, distance[vx.n]));
}
}
}

// Main method
public static void main(String argvs[])
{

int totalNodes = 9;
int s = 0;

// representation of the connected edges 
// using the adjacency list 
// by declaration of the List class object

// Declaring and object of the type List<Node>
List<List<Node> > adjacent = new ArrayList<List<Node> >();

// Initialize list for every node
for (int i = 0; i < totalNodes; i++) {
    List<Node> itm = new ArrayList<Node>();
    adjacent.add(itm);
}

// adding the edges
// The statement adjacent.get(0).add(new Node(1, 3)); means
// to travel from node 0 to 1, one has to cover 3 units of distance
// it does not mean one has to travel from 1 to 0
// To travel from 1 to 0, we have to add the statement 
// adjacent.get(1).add(new Node(0, 3));
// Note that the distance is the same i.e., 3 units in both the cases.
// Similarly, we have added other edges too.
 
adjacent.get(0).add(new Node(1, 3));
adjacent.get(0).add(new Node(7, 7));
adjacent.get(1).add(new Node(0, 3));
adjacent.get(1).add(new Node(2, 7));
adjacent.get(1).add(new Node(7, 10));
adjacent.get(1).add(new Node(8, 4));
adjacent.get(2).add(new Node(1, 7));
adjacent.get(2).add(new Node(3, 6));
adjacent.get(2).add(new Node(5, 2));
adjacent.get(2).add(new Node(8, 1));
adjacent.get(3).add(new Node(2, 6));
adjacent.get(3).add(new Node(4, 8));
adjacent.get(3).add(new Node(5, 13));
adjacent.get(3).add(new Node(8, 3));
adjacent.get(4).add(new Node(3, 8));
adjacent.get(4).add(new Node(5, 9));
adjacent.get(5).add(new Node(2, 2));
adjacent.get(5).add(new Node(3, 13));
adjacent.get(5).add(new Node(4, 9));
adjacent.get(5).add(new Node(6, 4));
adjacent.get(5).add(new Node(8, 5));
adjacent.get(6).add(new Node(5, 4));
adjacent.get(6).add(new Node(7, 2));
adjacent.get(6).add(new Node(8, 5));
adjacent.get(7).add(new Node(0, 7));
adjacent.get(7).add(new Node(1, 10));
adjacent.get(7).add(new Node(6, 2));
adjacent.get(7).add(new Node(8, 6));
adjacent.get(8).add(new Node(1, 4));
adjacent.get(8).add(new Node(2, 1));
adjacent.get(8).add(new Node(3, 3));
adjacent.get(8).add(new Node(5, 5));
adjacent.get(8).add(new Node(6, 5));
adjacent.get(8).add(new Node(7, 6));

// creating an object of the class DijkstraExample1
DijkstraExample1 obj = new DijkstraExample1(totalNodes);
obj.dijkstra(adjacent, s);

// Printing the shortest path to all the nodes
// from the source node
System.out.println("The shortest path from the node :");

for (int j = 0; j < obj.distance.length; j++)
{
    System.out.println(s + " to " + j + " is " + obj.distance[j]);
}
}
}

// The Node class implementing the Comparator interface
// The object of this class represents a node of the graph
class Node implements Comparator<Node> 
{

// Member variables of the Node class
public int n;
public int price;

// Constructors of this class

// Constructor 1
public Node() 
{
    
}

// Constructor 2
public Node(int n, int price)
{
this.n = n;
this.price = price;
}

@Override 
public int compare(Node n1, Node n2)
{

if (n1.price < n2.price)
{
return -1;
}
if (n1.price > n2.price)
{
return 1;
}

return 0;
}
}

Output:

The shortest path from the node:
0 to 0 is 0
0 to 1 is 3
0 to 2 is 8
0 to 3 is 10
0 to 4 is 18
0 to 5 is 10
0 to 6 is 9
0 to 7 is 7
0 to 8 is 7

The time complexity of the above implementation is O(V + E*log(V)), where V is the total number of vertices, and E is the number of Edges present in the graph.

Limitations of Dijkstra Algorithm

The following are some limitations of the Dijkstra Algorithm:

The Dijkstra algorithm does not work when an edge has negative values.
For cyclic graphs, the algorithm does not evaluate the shortest path. Hence, for the cyclic graphs, it is not recommended to use the Dijkstra Algorithm.