Display Unique Rows in a Binary Matrix in Java

In this section, we will discuss how one can display unique rows in a binary matrix in Java. In this problem, a binary matrix is given and we have to identify, and then print the unique rows of the given binary matrix.

Example 1: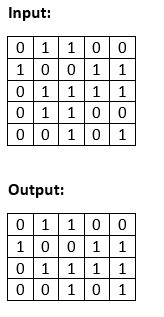

Explanation:

In the above input matrix, there are 5 rows:

R1 = {0, 1, 1, 0, 0}, and R2 = {1, 0, 0, 1, 1}, R3 = {0, 1, 1, 1, 1}, R4 = {0, 1, 1, 0, 0, 0}, and

R5 = {0, 0, 1, 0, 1}. In these 5 rows, rows R1 and R4 are identical, and the other rows are unique. Therefore, row R4 is discarded in the output.

Example 2: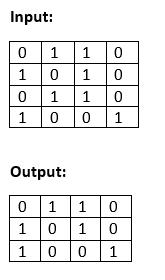

Explanation:

In the above input matrix, there are 4 rows:

R1 = {0, 1, 1, 0}, and R2 = {1, 0, 1, 0}, R3 = {0, 1, 1, 0}, and R4 = {1, 0, 0, 1}. In these 4 rows, row R1 and R3 are identical, and the rest other rows are unique. Therefore, the row R3 is discarded in the output.

Naive Approach

The naïve approach is simple. First, print the first row, then check the second-row matches with the printed row (first row) or not. If it matches, discard the second row; otherwise, print the second row. For the third row, check whether it matches the printed rows (first and second row) or not. If it does not match, do not print the third row; otherwise, print the third row. Treat the other rows in the same way.

Implementation Steps

The following are the steps that are required to implement the naïve approach.

Step 1: Traverse the elements of the matrix row-wise.

Step 2: For the current row, check whether it matches with any of the previous rows or not.

Step 3: If the current row matches with the previous rows, do not print the current row.

Step 4: Otherwise, display the current row.

Let's see the implementation of the above algorithm.

FileName: UniqueRowsMatrix.java

public class UniqueRowsMatrix
{
// method that prints all
// unique rows in a given matrix.
public void printUniqueRows(int matrix[][], int row, int col)
{
    // Traverse through the matrix
    for(int j = 0; j < row; j++)
    {
        // isUnqiue will get only 
        // two values, one is 0, and 
        // other is 1. 0 means the
        // row is not unique, and 1
        // means the row is unique
        int isUnqiue = 0;
        // Check whether there is a same column
        // that is already displayed, i.e if jth and
        // ith column match.
        for(int i = 0; i < j; i++)
        {
            isUnqiue = 0; 
            for(int k = 0; k < col; k++)
            {
                if (matrix[j][k] != matrix[i][k])
                {
                    isUnqiue = 1;
                }
            }
            if (isUnqiue == 0)
                break;
        } 
        // If the row is unique
        // or it is the first row
        if (isUnqiue == 1 || j == 0)
        {
            // display the row
            for(int p = 0; p < col; p++)
            {
                System.out.print(matrix[j][p] + " ");
            }
            System.out.println();
        }
    }
}
// main method
public static void main(String argvs[])
{
//creating an object of the class UniqueRowsMatrix
UniqueRowsMatrix obj = new UniqueRowsMatrix();

// input binary matrix
int matrix[][] = { { 0, 1, 1, 0, 0 },
                  { 1, 0, 0, 1, 1 },
                  { 0, 1, 1, 1, 1 },
                  { 0, 1, 1, 0, 0 },
                  { 0, 0, 1, 0, 1 }
                };
 
// row length of the matrix          
int row = matrix.length;

// column length of the matrix
int col = matrix[0].length;
System.out.println("For the following matrix: ");
for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
System.out.println();
System.out.println("The unique rows are: ");
obj.printUniqueRows(matrix, row, col);
System.out.println("\n");
// input binary matrix
int matrix1[][] = { { 0, 1, 1, 0 },
                  { 1, 0, 1, 0 },
                  { 0, 1, 1, 0 },
                  { 1, 0, 0, 1 }
                };
// row length of the matrix          
row = matrix1.length;
// column length of the matrix
col = matrix1[0].length;
System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(matrix1[i][j] + " ");
}
System.out.println();
}
System.out.println();
System.out.println("The unique rows are: ");
obj.printUniqueRows(matrix1, row, col);
 }
}

Output:

For the following matrix: 
0 1 1 0 0 
1 0 0 1 1 
0 1 1 1 1 
0 1 1 0 0 
0 0 1 0 1 

The unique rows are: 
0 1 1 0 0 
1 0 0 1 1 
0 1 1 1 1 
0 0 1 0 1 

For the following matrix: 
0 1 1 0 
1 0 1 0 
0 1 1 0 
1 0 0 1 

The unique rows are: 
0 1 1 0 
1 0 1 0 
1 0 0 1

Complexity Analysis: In the above program, we are comparing every row with the previously occurred row to check whether the row is unique or not. In the row comparison, we have to check every element of one row matches with the other row (column-size) or not. Therefore, the time complexity of the above program is O(R² x C), where R is the total rows present in the matrix and C is the total number of rows present in the matrix. As we are not using any auxiliary array in the program, therefore, the space complexity of the above program is constant, which is O(1).

If we observe the above program, we will find that there are many sub-problems that have been computed more than one time, leading to the exponential time complexity. Observe the following.

Approach: Using Binary Search Tree

In this approach, the first requirement is to compute the decimal equivalent of each row and push them into the binary search tree. Note that each node of the binary search tree fetches two fields: one for the decimal value, and the other for the row number.

Implementation Steps

The following are the steps required to implement the binary search tree approach.

Step 1: Create a Binary Search Tree where no duplicate node is stored.

Step 2: Create a method to change a row into the decimal and to change the decimal value into the binary array.

Step 3: Traverse the input matrix, and insert the row into the Binary Search Tree.

Step 4: Do an in-order traversal of the Binary Search Tree and change the decimal into the binary array, and then display it.

Let's see the implementation of the above algorithm.

FileName: UniqueRowsMatrix1.java

import java.util.*;
public class UniqueRowsMatrix1
{

  static class BST 
  {
    int val;
    BST lt, rt;
    BST(int val)
    {
      this.val = val;
      this.lt = this.rt = null;
    }
  }


  // converting array to decimal
  static int convertArr(int a[], int C)
  {
    int s = 0;
 
    for(int j = 0; j < C; j++)
    {
      s += Math.pow(2, j) * a[j];
    }
    
    return s;
  }
 
  // printing the column which is represented as the integers
  static void display(int p, int C)
  {
    for(int j = 0; j < C; j++)
    {
      System.out.print(p % 2 + " ");
      p = p / 2;
    }
    System.out.println();
  }
 
 
 
  // method that defines the insert.
  static BST Insert(BST rt, int val)
  {
    if(rt == null)
    {
      // Inserting the first node, if the root is null.
      return new BST(val);
    }
 
    //if the value is current
    if(val == rt.val)
    {
      return rt;
    }
 
    // Inserting the data.
    if(val > rt.val)
    {
      // Inserting the right node, if the 'value' that
      // has to be inserted is more than the 'rt' node value.
 
      // Processing the right nodes.
      rt.rt = Insert(rt.rt, val);
    }
    else
    {
      // Inserting the left node data, if the 'val' that
      // has to be inserted is more than the 'rt' node value.
 
      // Processing the left nodes.
      rt.lt = Insert(rt.lt, val);
    }
 
    // Returning 'rt' node, after the insertion.
    return rt;
  }
 
  // Inorder traversal of the BST.
  // It gives the data in sorted order.
  static void Inorder(BST rt, int C)
  {
    if(rt == null)
    {
      return;
    }
    Inorder(rt.lt, C);
    display( rt.val, C );
    Inorder(rt.rt, C);
  }
 
  // The main method that display
  // all the unique rows in the given matrix.
  static void printUniqueRows(int matrix[][], int R, int C)
  {
 
    BST b, rt = null;
 
    // Traversing the matrix
    for(int j = 0; j < R; j++)
    {
      // inserting the row into the BST
      rt = Insert(rt, convertArr(matrix[j], C));
    }
 
 
    //print
    Inorder(rt, C);
 
  }


// main method
public static void main(String argvs[])
{
//creating an object of the class UniqueRowsMatrix1
UniqueRowsMatrix1 obj = new UniqueRowsMatrix1();

// input binary matrix
int maxtrix[][] = { { 0, 1, 1, 0, 0 },
                  { 1, 0, 0, 1, 1 },
                  { 0, 1, 1, 1, 1 },
                  { 0, 1, 1, 0, 0 },
                  { 0, 0, 1, 0, 1 }
                };
 
// row length of the matrix          
int row = maxtrix.length;

// column length of the matrix
int col = maxtrix[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(maxtrix[i][j] + " ");
}
System.out.println();
}

System.out.println();
System.out.println("The unique rows are: ");
obj.printUniqueRows(maxtrix, row, col);
 
System.out.println("\n");


// input binary matrix
int matrix1[][] = { { 0, 1, 1, 0 },
                  { 1, 0, 1, 0 },
                  { 0, 1, 1, 0 },
                  { 1, 0, 0, 1 }
                };
 
// row length of the matrix          
row = matrix1.length;

// column length of the matrix
col = matrix1[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(matrix1[i][j] + " ");
}
System.out.println();
}

System.out.println();
System.out.println("The unique rows are: ");
obj.printUniqueRows(matrix1, row, col);
 


}
}

Output:

For the following matrix: 
0 1 1 0 0 
1 0 0 1 1 
0 1 1 1 1 
0 1 1 0 0 
0 0 1 0 1 

The unique rows are: 
0 1 1 0 0 
0 0 1 0 1 
1 0 0 1 1 
0 1 1 1 1

For the following matrix: 
0 1 1 0 
1 0 1 0 
0 1 1 0 
1 0 0 1 

The unique rows are: 
0 1 1 0 
1 0 1 0 
1 0 0 1

Complexity Analysis: In the above program, we are traversing each row and column of the matrix, which leads to the time complexity of O(R * C). Also, the time complexity of inserting a row in the binary search tree is O(R). As we are inserting each row, therefore the time consumed in insertion is R * O(log(R)). Thus, the overall time complexity of the above program is O(R * C + R * (log(R))). In the program, we are using the auxiliary space to store the binary search array leading to the space complexity of O(R), where R is the row size of the input matrix and C is the column size of the input matrix.

Approach: Using TRIE

In this approach, we will be using the TRIE data structure to find the unique rows. We know that the TRIE data structure is an efficient data structure for data retrieval. Using the TRIE data structure, the complexities of searching can be optimized. As we know that the input matrix is the binary matrix; therefore, we will be customizing the TRIE data structure a bit where each node will have two children one is for 1, and the other is for 0.

Implementation Steps

Step 1: Create a TRIE data structure for storing the row.

Step 2: Traverse through each row and insert it into the TRIE data structure created in the previous step. Since, TRIE can never contain any duplicate entries; therefore, when we traverse the duplicate row to insert it into the TRIE; it does not impact the TRIE data structure. Thus, whatever is present in the TRIE, after each row of the input matrix is traversed, are the unique rows.

Step 3: Traverse the TRIE data structure and display the rows.

Let's see the implementation of the above algorithm.

FileName: UniqueRowsMatrix2.java

// An implementation of the insert and search operations
// on the Trie Data structure
public class UniqueRowsMatrix2 {
	
	// The count is 2 as we are dealing in 1's and 2's
	static final int CNT = 2;
	
	// trie node
	static class TNode
	{
		TNode[] children = new TNode[CNT];
	
		// isEndOfRow is true if and only if the node represents
		// the end of the row
		boolean isEndOfRow;
		
		TNode(){
			isEndOfRow = false;
			for (int j = 0; j < CNT; j++)
				children[j] = null;
		}
	};
	
	static TNode rt;
	
	// If not present, inserts key into trie
	// If the key is prefix of trie node,
	// just marks leaf node
	static boolean insert(int row[])
	{
		int lvl;
		int size = row.length;
		int idx;

		TNode pCrawl = rt;
		
		boolean isUnique = false;
	
	    // from every node we have the two options to follow
	    // one to follow the 1's and the other is to 
	    // follow the 0's. What we are going to follow 
	    // is decided by the number present in the row[] array
		for (lvl = 0; lvl < size; lvl++)
		{
		    // idx will be always 0 and 1
			idx = row[lvl];
			
			
			// it is this if block that makes the TRIE to 
			// discard the redundant rows
			
			// the if block checks whether the path has been 
			// traversed earlier or not. If yes, then no any new
			// node is created. If not traversed, then a new node is created
			if (pCrawl.children[idx] == null)
			{
				pCrawl.children[idx] = new TNode();
				isUnique = true;
			}
	
			pCrawl = pCrawl.children[idx];
		}
	
		// marking the last node as the leaf node
		pCrawl.isEndOfRow = true;
		
		return isUnique;
	}
	
	// A utility method for displaying the unique rows
    void displayRow(int input[][], int row)
    {
        int j;
        int colSize = input[0].length;
        for(j = 0; j < colSize; ++j)
        {
            System.out.print(input[row][j] + " ");
        }
        System.out.println();
    }
    
    
    
    // it is the method that is being invoked
    // by the main() method. The method filters out the unique 
    // rows from the input matrix and displays it by invoking the 
    // displayRow() method
    void filterAndPrintUniqueRows(int input[][], int R, int C)
    {
        rt = new TNode(); // creating an empty Trie
        int j;
     
        // Iterating through all of the rows
        for (j = 0; j < R; ++j)
         
            // inserting row into the TRIE
            if (insert(input[j]))
            {
                // a unique row is found, display it
                displayRow(input, j);
            }
    }
	
	// main method
public static void main(String argvs[])
{
//creating an object of the class UniqueRowsMatrix2
UniqueRowsMatrix2 obj = new UniqueRowsMatrix2();

// input binary matrix
int maxtrix[][] = { { 0, 1, 1, 0, 0 },
                  { 1, 0, 0, 1, 1 },
                  { 0, 1, 1, 1, 1 },
                  { 0, 1, 1, 0, 0 },
                  { 0, 0, 1, 0, 1 }
                };
 
// row length of the matrix          
int row = maxtrix.length;

// column length of the matrix
int col = maxtrix[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(maxtrix[i][j] + " ");
}
System.out.println();
}

System.out.println();
System.out.println("The unique rows are: ");
obj.filterAndPrintUniqueRows(maxtrix, row, col);
 
System.out.println("\n");


// input binary matrix
int matrix1[][] = { { 0, 1, 1, 0 },
                  { 1, 0, 1, 0 },
                  { 0, 1, 1, 0 },
                  { 1, 0, 0, 1 }
                };
 
// row length of the matrix          
row = matrix1.length;

// column length of the matrix
col = matrix1[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(matrix1[i][j] + " ");
}
System.out.println();
}

System.out.println();
System.out.println("The unique rows are: ");
obj.filterAndPrintUniqueRows(matrix1, row, col);
 


}
}

Output:

For the following matrix: 
0 1 1 0 0 
1 0 0 1 1 
0 1 1 1 1 
0 1 1 0 0 
0 0 1 0 1 

The unique rows are: 
0 1 1 0 0 
0 0 1 0 1 
1 0 0 1 1 
0 1 1 1 1

For the following matrix: 
0 1 1 0 
1 0 1 0 
0 1 1 0 
1 0 0 1 

The unique rows are: 
0 1 1 0 
1 0 1 0 
1 0 0 1

Complexity Analysis: In the above program, we are traversing each row and column of the matrix, which leads to the time complexity of O(R * C). In the program, we are using the auxiliary space to store the TRIE data structure leading to the space complexity of O(R * C), where R is the row size of the input matrix and C is the column size of the input matrix.

Approach: Using HashSet

In this approach, we will use the HashSet data structure to find the unique rows. We know that the HashSet data structure implements the Set interface. Therefore, there cannot be any duplicate data present in the HashSet. The approach is to convert each row of the HashSet into String and insert it into the HashSet.

Implementation Steps

Step 1: Create a HashSet data structure for storing the row.

Step 2: Traverse through each row and insert it into the Hash data structure created in the previous step. Since, HashSet can never contain any duplicate entries; therefore, when we traverse the duplicate row to insert it into the HashSet, it does not impact the HashSet data structure. Thus, whatever is present in the HashSet, after each row of the input matrix is traversed, are the unique rows. Note that before inserting the row in the HashSet, convert it into the String. For Example,

For the following row: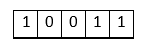

We will have the String as "10011".

Step 3: Traverse the HashSet data structure and display the rows.

Let's see the implementation of the above algorithm.

FileName: UniqueRowsMatrix3.java

// importing inbuilt HashSet
import java.util.HashSet;

public class UniqueRowsMatrix3 {
	
    public void filterAndPrintUniqueRows(int input[][], int R, int C)
    {
        // creating an obejct of the HashSet class
        HashSet<String> hs = new HashSet<String>();
         
        for(int j = 0; j < R; j++)
        {
            // for stroing the string generated from the row
            // of the input matrix
            String str = "";
             
             
            // loop for converting the row into a string 
            for(int i = 0; i < C; i++)
            {
                str = str + String.valueOf(input[j][i]);
            }
            
            
            if(!hs.contains(str)) 
            {
                hs.add(str);
                
                int size = str.length();
                
                // displaying the unique row
                for(int i = 0; i < size; i++)
                {
                    System.out.print(str.charAt(i) + " ");
                }
                
                System.out.println();
                 
            }
        }
    }
	
	// main method
public static void main(String argvs[])
{
//creating an object of the class UniqueRowsMatrix3
UniqueRowsMatrix3 obj = new UniqueRowsMatrix3();

// input binary matrix
int maxtrix[][] = { { 0, 1, 1, 0, 0 },
                  { 1, 0, 0, 1, 1 },
                  { 0, 1, 1, 1, 1 },
                  { 0, 1, 1, 0, 0 },
                  { 0, 0, 1, 0, 1 }
                };
 
// row length of the matrix          
int row = maxtrix.length;

// column length of the matrix
int col = maxtrix[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(maxtrix[i][j] + " ");
}
System.out.println();
}

System.out.println();
System.out.println("The unique rows are: ");
obj.filterAndPrintUniqueRows(maxtrix, row, col);
 
System.out.println("\n");


// input binary matrix
int matrix1[][] = { { 0, 1, 1, 0 },
                  { 1, 0, 1, 0 },
                  { 0, 1, 1, 0 },
                  { 1, 0, 0, 1 }
                };
 
// row length of the matrix          
row = matrix1.length;

// column length of the matrix
col = matrix1[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(matrix1[i][j] + " ");
}
System.out.println();
}

System.out.println();
System.out.println("The unique rows are: ");
obj.filterAndPrintUniqueRows(matrix1, row, col);
 


}
}

Output:

For the following matrix: 
0 1 1 0 0 
1 0 0 1 1 
0 1 1 1 1 
0 1 1 0 0 
0 0 1 0 1 

The unique rows are: 
0 1 1 0 0 
0 0 1 0 1 
1 0 0 1 1 
0 1 1 1 1

For the following matrix: 
0 1 1 0 
1 0 1 0 
0 1 1 0 
1 0 0 1 

The unique rows are: 
0 1 1 0 
1 0 1 0 
1 0 0 1

Complexity Analysis: In the above program, we are traversing each row and column of the matrix, which leads to the time complexity of O(R * C). In the program, we are using the auxiliary space to store the Hash data structure leading to the space complexity of O(R * C), where R is the row size of the input matrix and C is the column size of the input matrix.

Next TopicRotate A Matrix By 180 Degree in Java

← prev next →