Dyck Path in Java

In Java programming, Dyck paths are a way to explore grids in a specific manner. Consider a square grid in which you wish to reach the top-right corner while keeping above a diagonal line. The idea is to see how many different pathways you may utilize to get there.

Consider a n × n square grid with the top-left corner indexed as (0, 0). A Dyck path is a unique walk that begins in the bottom-left corner (n-1, 0) and ends in the top-right corner (0, n-1). The route must always stay above the diagonal line that runs from the grid's bottom left to the top right.

The objective here is to determine and count the total number of Dyck Paths that match these conditions, namely those that connect points (n-1, 0) to (0, n-1).

Example 1:

Input: n = 1

Output: 1

Example 2:

Input: n = 4

Output: 14

Example 3:

Input: n = 6

Output: 132

Example 4:

Input: n = 8

Output: 1430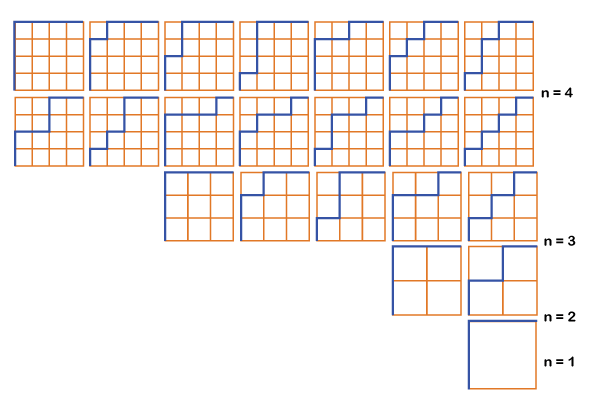

Approach: Using Catalan Number

The approach to counting Dyck paths is based on the Catalan number formula:

C_n = (2n)! / [(n + 1)! * n!]

The formula represents the count of Dyck paths with a length of 2n, originating from the point (n-1, 0) and concluding at the point (0, n-1). Another way to express this is through the product:

C_n = Π (n + k) / k, for k = 2 to n

Where n is a non-negative integer, and k iterates from the range of 2 to n. This formula efficiently calculates the count of valid Dyck paths by leveraging the properties of Catalan numbers

Algorithm

Step 1: Start with the main method.

Step 2: Initialize an integer variable n with the desired length of Dyck paths.

Step 3: Call the countDyckPaths method with n as the argument.

Step 4: Inside the countDyckPaths method:

Check if n is less than 0. If so, return 0 because Dyck paths cannot have negative lengths.
Call the calculateCatalanNumber method with n as the argument.
Return the calculated Catalan number as the count of Dyck paths.

Step 5: Inside the calculateCatalanNumber method:

Determine whether n is less than or equal to 1. If yes, because the 0th and 1st Catalan numbers are both 1, return 1.
Initialize a Catalan variable to 1.
Use a loop to calculate the numerator and denominator components of the Catalan number using the formula Cn = (2n)! / ((n + 1)! * n!).
- Multiply Catalan by (2 * n - i) in each iteration to calculate the numerator.
- Divide Catalan by (i + 1) in each iteration to calculate the denominator.
After the loop, divide Catalan by (n + 1) to get the final value of Cn.
Return the calculated Catalan number.

Step 6: Print the result obtained in the main method, indicating the number of Dyck paths of the specified length.

Implementation:

Filename: DyckPathsUsingCatalan.java

public class DyckPathsUsingCatalan {
    public static void main(String[] args) {
        int n = 4; // Replace with the specified value of n

        // Calculate the number of Dyck paths using Catalan numbers
        long count = countDyckPaths(n);

        // Print the result
        System.out.println("Number of Dyck paths of length " + n + ": " + count);
    }

    // Function to calculate the nth Catalan number
    public static long calculateCatalanNumber(int n) {
        if (n <= 1) {
            return 1;
        }

        long catalan = 1;
        for (int i = 0; i < n; i++) {
            // Calculate the numerator (2n)!
            catalan *= (2 * n - i);
            // Calculate the denominator ((n + 1)! * n!)
            catalan /= (i + 1);
        }

        return catalan / (n + 1); // Calculate Cn = (2n)! / ((n + 1)! * n!)
    }

    // Function to count Dyck paths of length n using Catalan numbers
    public static long countDyckPaths(int n) {
        if (n < 0) {
            return 0;
        }

        return calculateCatalanNumber(n); // Calculate the nth Catalan number
    }
}

Output:

Number of Dyck paths of length 4: 14

Time Complexity: The time complexity of the above code is O(n), where n is the input value for which you want to calculate the number of Dyck paths. It is because the calculateCatalanNumber method iterates over the range of values from 0 to n, performing constant time operations in each iteration.

Auxiliary Space: The auxiliary space complexity of the code is O(1), which means it uses a constant amount of additional space regardless of the input value n.

Approach: Direct Combinatorial

A direct combinatorial approach, as used in the provided code, calculates mathematical structures, such as Catalan numbers, without explicitly generating them. It directly computes the desired result using combinatorial formulas, avoiding the need to traverse or generate individual instances of the structures.

Algorithm:

Step 1: Start with the main method.

Step 2: Initialize an integer variable length with the desired length of Dyck paths.

Step 3: Call the countDyckPaths method with length as the argument.

Step 4: Inside the countDyckPaths method:

Define a variable numerator and calculate it by calling the calculateFactorial method with 2 * n as the argument.
Declare a variable named denominator and compute its value by performing the product of two separate function calls to calculateFactorial. One of these calls should have n + 1 as its argument, and the other should have n as its argument.
Calculate the result by dividing the numerator by the denominator.
Return the calculated result as the count of Dyck paths of length n.

Step 5: Inside the calculateFactorial method:

Initialize an integer variable result to 1.
Use a loop that iterates from 1 to the input number.
In each iteration, multiply the result by the loop variable i.
Return the final value of the result as the factorial of the input number.

Step 6: Print the result obtained in the main method, indicating the number of Dyck paths with the specified length.

Implementation:

Filename: DyckPathCounter.java

import java.util.*;

public class DyckPathCounter {

    // Function to calculate the factorial of a given number
    public static int calculateFactorial(int number) {
        int result = 1;
        for (int i = 1; i <= number; i++) {
            result *= i;
        }
        return result;
    }

    // Function to calculate the number of Dyck paths of length n using the second approach
    public static int countDyckPaths(int n) {
        // Calculate the numerator of the formula
        int numerator = calculateFactorial(2 * n);
        
        // Determine the denominator of the formula
        int denominator = calculateFactorial(n + 1) * calculateFactorial(n);
        
        // Divide the numerator by the denominator to obtain the result
        return numerator / denominator;
    }

    public static void main(String[] args) {
        int length = 4;

        // Display the number of Dyck paths of the given length
        System.out.println("The number of Dyck paths with a length of " + length + " is: " + countDyckPaths(length));
    }
}

Output:

The number of Dyck paths with a length of 4 is: 14

Time Complexity: The time complexity of the provided code is O(n) since the most time-consuming operation involves calculating factorials. The calculation is achieved through a loop that iterates from 1 to 'n'. As each iteration of the loop adds a proportional amount of work, the overall time complexity grows linearly with the input size 'n,' resulting in an O(n) time complexity.

Auxiliary space: The code's auxiliary space complexity is O(1) as it employs a fixed amount of extra memory to store variables, irrespective of the input value 'n'. Variables such as numerator, denominator, and result occupy a consistent amount of space, and this allocation remains constant regardless of the magnitude of 'n'. Consequently, the auxiliary space complexity does not rely on the input size.

Next TopicFind the last two digits of the Factorial of a given Number in Java

← prev next →