Fenwick Tree in Java

In this section, we are going to learn about the Fenwick tree in Java. Fenwick tree is also called Binary Indexed Tree (BIT).

Scenario Where Fenwick Tree is Used

Let's understand in which scenario a segment tree comes in handy.

Suppose, we have an array a[] = {0, 1, …, s - 1} and want to perform the following two tasks on the given array:

• Computing the sum of the array elements from the index m to n, where 0 <= m <= n <= s - 1
• Changing the value of an element of the array a[] to a new value nv, i.e., one is required to do a[j] = nv, where 0 <= j <= s - 1.

In order to find the solution of the above two tasks, we can use either Segment Tree or Fenwick tree. The Segment tree provides the optimized solution. Similar to the Segment tree, the Fenwick tree can also be represented using an array. The benefit of the Fenwick tree is that it is easy to code and acquires less space as compared to the Segment tree.

Note: It is advised to go through the topic Segment Tree in Java first for a better understanding of the Fenwick tree.

Representation of Fenwick Tree Using Array

As stated above, the Fenwick tree is represented using an array. Let the fenArr[] array does the representation of the Fenwick tree. Each and every node of the Fenwick tree contains the sum of some of the elements of the input array. The size of the Fenwick Tree is the same as the size of the input array (which is s in our case).

Construction of Fenwick Tree Using Array

First, we allocate the memory for the fenArr[] array and then initialize that array with the values as 0. After that, we can perform various operations on that array.

Operations on Fenwick Tree

Computing sum a sub-array of the given input array a[]: To achieve the sum of elements of the subarray, we implement the method getArrSum(y).

getArrSum(y): Returns the sum of the sub-array ar[0, …, y] using the fenArr[] that is constructed using the input array a[0, …, n].

Step 1: Do initialize the resultant total as 0 and the current index as y + 1.

Step 2: Repeat steps a & b until the current index is > 0.

1. Add fenArr[idx] to the sum.
2. Go to the parent of fenTree[idx]. The parent can be reached by truncating the last set bit from the current index, i.e., idx = idx - (idx & (-idx))

Step 3: Return the sum.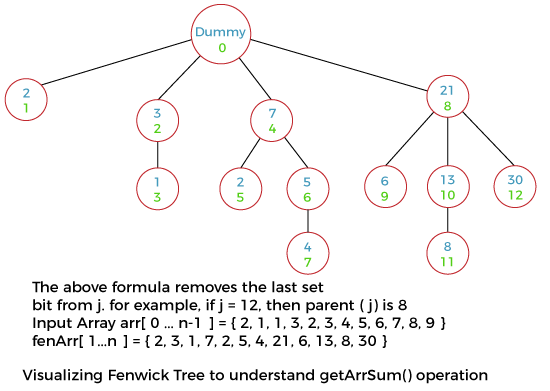

Updating the value at a particular index: To achieve the updation at a particular index, we implement the method updateFenwick(). Note that updating the value at a particular index does not create any impact on the input array a[]. It only creates an impact on the fenArr[] array.

updateFenwick(y, v): The method updates the value at the index y with the value u.

Step 1: Assign the value y + 1 to the current index.

Step 2: Repeat steps a and b until the current index is equal to or less than s.

1. Add the value v to the fenArr[idx].
2. Go to the next element of the fenArr[idx]. By setting the last set bit of the current index one can find the next element that is, idx = idx + (idx & (-idx)).

Working of a Fenwick Tree

We know that any positive number can be represented as a sum of powers of 2, and this idea has been used in the Fenwick tree. For example, 21 can be written as 2⁴ + 2² + 2⁰ = 16 + 4 + 1. Each node of the Fenwick tree contains the sum of p elements, where p is a power of 2. Consider the above diagram (the diagram for getArrSum() operation), the resultant sum of the first 12 elements can be achieved by the addition of the 4 elements from the last (from 9 to 12) plus the summation of the first 8 elements (from 1 to 8). In the binary representation, the total number of bits of a number n that are set is O(log(n)). Therefore, one needs to do the traversal of at-most O(log(n)) nodes in both getArrSum() and updateFenwick() operations. Thus, the time complexity of the construction is O(n * log(n)) as the updateFenwick() operation is invoked for all of the n elements.

Implementation of the Fenwick Tree

Let's implement the Fenwick Tree along with the operations defined above.

FileName: FenwickTreeExample.java

Output:

Sum of the elements in array a[0 ... 6] is: 161
Sum of the elements in array a[0 ... 6] after update is: 168