Figurate Number in Java

A figurate number is the classical source of number sequence. In this section, we will learn what is a figurate number and also create Java programs to check if the given number is a figurate number or not. The figurate number program is frequently asked in Java coding interviews and academics.

Figurate or figural numbers have a rich history with many applications. In general, a figurate number is a number that can be represented by regular and discrete geometric patterns with equally spaced points. It may be, a polygonal, polyhedral, or polytopic number if the arrangement of points forms a regular polygon, a regular polyhedron, or a regular polytope, respectively.

Figurate numbers can also form other geometric shapes such as centered polygons, L-shapes, three-dimensional (and multidimensional) solids, etc.

Figurate Number

It is the number of triangles (all of whose vertices lie inside the circle) formed when n points in general position on a circle are joined by straight lines.

A figurate number, also known as a figural number. It is a number that can be represented by a regular geometrical arrangement of equally spaced points. If the arrangement forms aregular polygon, the number is called apolygonal number. The following table describes the figurate numbers with their sequence.

Let' see their pictorial representation of the figurate number. The following figure illustrates the same.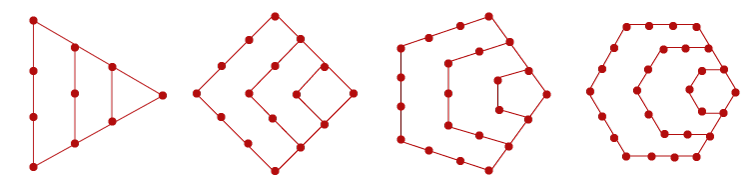

The polygonal numbers illustrated above are calledtriangular, square, pentagonal, and hexagonal numbers, respectively.

It is based on a 6-dimensional regular simplex. It is an OEIS sequence A000579. It is also known as binomial coefficient C(n, 6).

According to Hyun Kwang Kim, it appears that every non-negative integer can be represented as the sum of g = 13 of these numbers.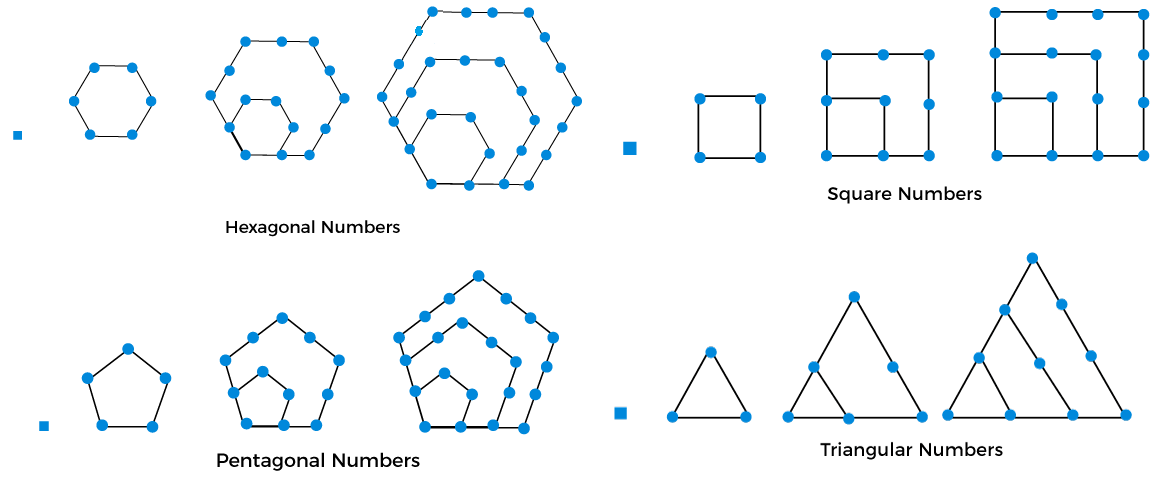

Properties

• a(n) is the number of terms in the expansion of (a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7)^n. The only prime in this sequence is 7.
• 6-dimensional triangular numbers, sixth partial sums of binomial transform of [1, 0, 0, 0, ...].
• a(n) = fallfac(n, 6)/6! is also the number of independent components of an antisymmetric tensor of rank 6 and dimension n >= 1. Here, fallfac is the falling factorial.
• Number of orbits of Aut(Z^7) as a function of the infinity norm n of the representative integer lattice point of the orbit, when the cardinality of the orbit is equal to 645120.
• For a set of integers {1,2,...,n}, a(n) is the sum of the 2 smallest elements of each subset with 5 elements that is 3*C(n+1,6) (for n>=5), hence a(n) = 3*C(n+1,6) = 3*A000579(n+1).
• a(n) = A000292(n-5)*A000292(n-2)/20

Formulas to Calculate Figurate Number

• General Formula: x^6/(1-x)^7
• Exponential Formula: exp(x)*x^6/720
• Conjecture: a(n+3) = Sum{0 <= k, l, m <= n; k + l + m <= n} k*l*m

Some other formulas are:

• a(n) = (n^6 - 15*n^5 + 85*n^4 - 225*n^3 + 274*n^2 - 120*n)/720.
• a(n) = 3*C(n+1, 6)

The above formulas lead to a conjecture a formula for a general N-agonal number:

Note: The above formula works only for N=2, 3, and 4.

Figurate Number Example

For example, consider a set of integers Z = {1, 2, 3, 4, 5, 6}. Let's apply the fifth property to find the figurate number.

From the given set Z, create subsets that must have five elements in each. We get:

{1, 2, 3, 4, 5}, {1, 2, 3, 4, 6}, {1, 2, 3, 5, 6}, {1, 2, 4, 5, 6}, {1, 3, 4, 5, 6}, {2, 3, 4, 5, 6}

From the above subsets, determine the smallest two numbers and add them together. That is:

a(6) = (1+2) + (1+2) + (1+2) + (1+2) + (1+3) + (2+3) = 21

Similarly, we can use the formula a(n) = 3*C(6+1,6) for the same. Let's put the values of n=6 in the formula, we get:

a(6) = 21 = 3*C(6+1,6)

Let's use another formula to check whether the number 84 is a figurate number or not.

a(9) = (1, 3, 3, 1). (1, 6, 15, 20) = (1 + 18 + 45 + 20) = 84

Hence, the 9^th figurate number is 84.

First few figurate numbers are:

0, 0, 0, 0, 0, 0, 1, 7, 28, 84, 210, 462, 924, 1716, 3003, 5005, 8008, 12376, 18564, 27132, 38760, 54264, 74613, 100947, 134596, 177100, 230230, 296010, 376740, 475020, 593775, 736281, 906192, 1107568, 1344904, 1623160, 1947792, 2324784, 2760681, 3262623

Using Successive Difference Method

We can calculate the figurate number using successive differences. For example, consider the following nonagonal numbers.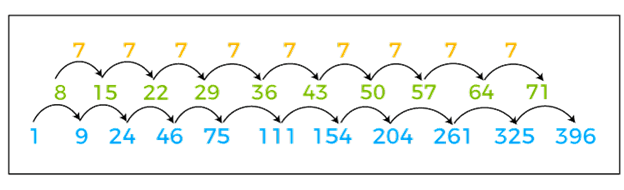

But the above method is not always helpful.

Types of Figurate Number

4-dimensional Figurate Numbers (A002417)

It can be calculated by using the following formulas:

It is an OEIS sequence A002417.

First few 4-dimesional figurate numbers are:

1, 8, 30, 80, 175, 336, 588, 960, 1485, 2200, 3146, 4368, 5915, 7840, 10200, 13056, 16473, 20520, 25270, 30800, 37191, 44528, 52900, 62400, 73125, 85176, 98658, 113680, 130355, 148800, 169136, 191488, 215985, 242760, 271950, 303696, 338143, 375440, 415740.

Properties

• a(n) is 1/6 the number of colorings of a 2 X 2 hexagonal array with n+2 colors.

• a(n) is the sum of all numbers that cannot be written as t*(n+1) + u*(n+2) for nonnegative integers t, u.
• a(n) is the total number of rectangles (including squares) contained in a stepped pyramid of n rows (or of base 2n-1) of squares.
• a(n) equals -1 times the coefficient of x^3 of the characteristic polynomial of the (n + 2) X (n + 2) matrix with 2's along the main diagonal and 1's everywhere else.
• a(n) is the n-th antidiagonal sum of the convolution array.
• Also, the number of 3-cycles in the (n+2)-triangular graph.

Formulas to Calculate 4-dimesional Figurate Number

• General Formula: x*(1+3*x)/(1-x)^5
• a(n) = C(n+2, 2)*n^2/3
• a(n) = C(n+3, n)*C(n+1, 1)
• a(n) = (binomial(n+3, n-1) - binomial(n+2,n-2))*(binomial(n+1,n-1) - binomial(n,n-2))
• a(n) = 5*a(n-1) -10*a(n-2) +10*a(n-3) -5*a(n-4) +a(n-5), n>5
• a(n) = A080852(4, n-1)
• a(n) = A000332(n+3) + 3*A000332(n+2)

4-Dimensional Figurate Number (A002418)

There is another formula to calculate 4-dimensional figurate number that is:

It is an OEIS sequence A002418.

First few figurate numbers of the sequence A002418 are:

0, 1, 9, 35, 95, 210, 406, 714, 1170, 1815, 2695, 3861, 5369, 7280, 9660, 12580, 16116, 20349, 25365, 31255, 38115, 46046, 55154, 65550, 77350, 90675, 105651, 122409, 141085, 161820, 184760, 210056, 237864, 268345, 301665, 337995.

Properties

• The sequence A002418 is the partial sum of A002413.
• Principal diagonal of the convolution array A213550, for n>0.
• Convolution of A000027 with A000566.

Formulas to Calculate Figurate Number of the Sequence A002418

• General Formula: x*(1+4*x)/(1-x)^5
• Exponential Formula: x*(24 + 84*x + 44*x^2 + 5*x^3)*exp(x)/4!

Other formulas are:

• a(n) = n*C((n+3),4)) - (n-1)*C((n+2),4)) or a(n) = A128064* A000332.
  For example, a(5) = 5*C(8,4) - 4*C(7,4) = 5*70 - 4*35 =210.
• a(0)=0, a(1)=1, a(2)=9, a(3)=35, a(4)=95 then a(n) = 5*a(n-1) - 10*a(n-2) + 10*a(n-3) - 5*a(n-4) + a(n-5)
• a(n) = A080852(5, n-1)

4-Dimensional Figurate Number (A002419)

There is another formula to calculate 4-dimensional figurate number of the sequence A002419. We can calculate it by using the following formula:

First few figurate numbers of the sequence A002419 are:

1, 10, 40, 110, 245, 476, 840, 1380, 2145, 3190, 4576, 6370, 8645, 11480, 14960, 19176, 24225, 30210, 37240, 45430, 54901, 65780, 78200, 92300, 108225, 126126, 146160, 168490, 193285, 220720, 250976, 284240, 320705, 360570, 404040, 451326

Properties

• a(n) is the n-th antidiagonal sum of the convolution array A213761.
• a(n) = the sum of all the ways of adding the k-tuples of A016777(0) to A016777(n-1).

Suppose, we have to calculate n=4. The terms are 1,4,7,10 giving (1)+(4)+(7)+(10)=22; (1+4)+(4+7)+(7+10)=33; (1+4+7)+(4+7+10)=33; (1+4+7+10)=22; on adding 22+33+33+22, we get 110 that is a figurate number.

Formulas to Calculate Figurate Number of the Sequence A002419

• a(n) = (3*n-1)*binomial(n+2, 3)/2
• General Formula: x*(1+5*x)/(1-x)^5
• Exponential Formula: x*(12 + 48*x + 26*x^2 + 3*x^3)*exp(x)/12.
• a(n) = (3*n^4 + 8*n^3 + 3*n^2 - 2*n)/12
• a(n) = A080852(6, n-1)

Regular Figurative Number (A090466)

The sorted k-gonal numbers of order greater than 2. If one were to include either the rank 2 or the 2-gonal numbers, then every number would appear. It is also known as polygonal numbers. It is an OEIS sequence A090466.

Number of terms less than or equal to 10^k for k = 1, 2, 3, ...: 3, 57, 622, 6357, 63889, 639946, 6402325, 64032121, 640349979, 6403587409, 64036148166, 640362343980, and so on.

For all squares (A001248) of primes p >= 5 at least one a(n) exists with p^2 = a(n) + 1. Thus the subset P_s(3) of rank 3 only is sufficient.

Proof:

For p >= 5, p^2 == 1 (mod {3,4,6,8,12,24}) and also P_s(3) + 1 = 3*s - 2 == 1 (mod 3). Thus the set {p^2} is a subset of {P_s(3) + 1}.

For all primes p > 5, at least one polygonal number exists with P_s(k) + 1 = p when k = 3 or 4, dependent on p mod 6.

Numbers m such that r = (2*m/d - 2)/(d - 1) is an integer for some d, where 2 < d < m is a divisor of 2*m. If r is an integer, then m is the d-th (r+2)-gonal number.

First few numbers of the sequence A090466 are:

6, 9, 10, 12, 15, 16, 18, 21, 22, 24, 25, 27, 28, 30, 33, 34, 35, 36, 39, 40, 42, 45, 46, 48, 49, 51, 52, 54, 55, 57, 58, 60, 63, 64, 65, 66, 69, 70, 72, 75, 76, 78, 81, 82, 84, 85, 87, 88, 90, 91, 92, 93, 94, 95, 96, 99, 100, 102, 105, 106, 108, 111, 112, 114, 115, 117, 118.

Figurate Number Java Program

The following Java program check whether the give number is a square number or not.

FigurateNumberExample1.java

Output:

Enter a number: 100
100.0 is a square number.

Let's create another Java program for a figurate number called nonagonal number.

NonagonalNumberExample.java

Output:

Enter the term you want to find: 4
The 4 rd/th nonagonal number is: 46