Find Saddle Point of a Matrix in Java

In this section, we will understand what is saddle point in a matrix, and how to find the saddle point of a matrix through a Java program.

What is the saddle point in a matrix?

In a matrix, an element is called the saddle point that is the minimum (or smallest) element row-wise and maximum (or largest) element column-wise. The term saddle point is widely used in game theory.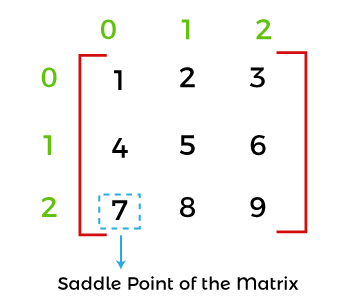

Note that a matrix may have more than one, and may not have saddle points. For example, consider the following matrix.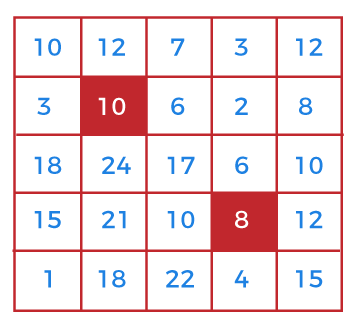

In the above matrix, 10 and 8 are the lowest in the respective column and highest in the respective row. Hence, the above matrix has two saddle points.

In the following matrix, there is no saddle point exists.

Algorithm

Traverse each row of the matrix one by one and find the minimum elements from each row.
Traverse the same column for finding the maximum element in which the minimum element is found.
If the minimum element in the row and maximum element in the column are the same, the element is the saddle point of the matrix.
If the minimum element in the row and maximum element in the column are not the same, there does not exist a saddle point.
Repeat the above steps until we do not get the saddle point.

How to find saddle point?

Consider the following matrix and find the saddle point.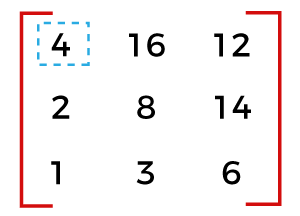

Let's find the saddle point.

Row 0: Minimum in row 0 is 4 (at index 0) and maximum in same column 0 is 7. Both elements are different, so row 0 does not contain any saddle point.

Row 1: Minimum in row 1 is 7 (at index 0) and maximum in same column 0 is 7. Both elements are the same, so 7 is the saddle point of the matrix.

Row 2: Minimum in row 2 is 1 (at index 1) and maximum in same column 1 is 8. Both elements are different, so row 2 does not contain any saddle point.

Java Program to Find the Saddle Point in a Matrix

FindSaddlePoint.java

public 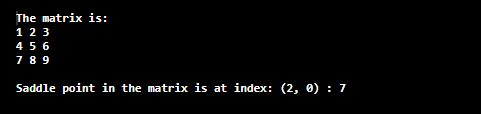class FindSaddlePoint
{
public static void main(String args[])
{
//initializing a matrix
int[][] matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
int m = 3, k;
//variables to store min and max elements 
int min = 0, max = 0;
int [][]index = new int[3][3];
System.out.print("The matrix is: \n");
int i,j;
//prints the given matrix
//outer loop for rows
for (i = 0; i < m; i++)
{
//inner loop for columns
for (j = 0; j < m; j++)
{
//prints the element of the matrix
System.out.print(matrix[i][j] + " " );
}
//throws cursor to the next line
System.out.println();
}
//logic to find the saddle points in the given matrix
//finds the minimum element in the row
for (i = 0; i < m; i++)
{
min = matrix[i][0];
for (j = 0; j < m; j++)
{
if (min >= matrix[i][j])
{
min = matrix[i][j];
index[0][0] = i;
index[0][1] = j;
}
}
//finds the maximum element in the same column
j = index[0][1];
max = matrix[0][j];
for (k = 0; k < m; k++)
{
if (max <= matrix[k][j])
{
max = matrix[i][j];
index[1][0] = k;
index[1][1] = j;
}
}
//saddle point is the minimum of a row and maximum of the column 
if (min == max) 
{
if (index[0][0] == index[1][0] && index[0][1] == index[1][1])
{
System.out.print("\nSaddle point in the matrix is at index: (" + index[0][0] + ", " + index[0][1] + ") : " + max + "\n");
}
}
}
}
}

Output:

Let's see another logic.

MatrixSaddlePoint.java

public class MatrixSaddlePoint
{
public static void main(String args[]) 
{
//creating a constructor of the class    
new MatrixSaddlePoint();
}
public MatrixSaddlePoint() 
{
//initializing an array    
int[][] matrix = {{4, 5, 6}, {7, 18, 9}, {5, 1, 3}};
//function calling 
findSaddlePoint(matrix);
}
//function to find the saddle point
private void findSaddlePoint(int[][] matrix) 
{
for (int i = 0; i < matrix.length; i++) 
{
boolean isSadlePointExist= true;
int minimum = matrix[i][0];
int colIndexOfRowMinimum = 0;
//finds minimum in row
for(int j=1; j< matrix[0].length; j++)
{
if(matrix[i][j] < minimum)
{
minimum = matrix[i][j];
colIndexOfRowMinimum = j; 
}
}
//find maximum in same column
for (int j = 0; j < matrix.length; j++) 
{
if(minimum < matrix[j][colIndexOfRowMinimum])
{
//if the above condition becomes true set saddle point to false    
isSadlePointExist = false;
break;
}
}
if(isSadlePointExist)
{
//prints the saddle point    
System.out.println("The saddle point of the matrix is: "+minimum);
}
}
}
}

Output: