Find the Good Matrix Problem in Java

Given a 2-dimensional array ARR with N rows and M columns, where each element contains a value of 0 or 1, convert the given matrix into a Good matrix. In a Good matrix, if an element is 0, all elements in its row and column should also be 0.

For example, if arr is the following matrix: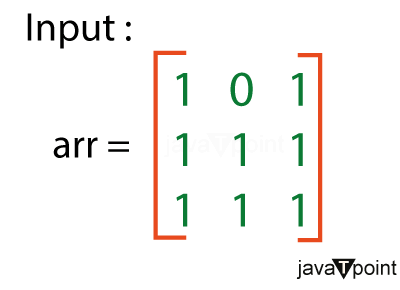

Input Format:

The first line of the input contains an integer, T, denoting the number of test cases. For each test case, the first line contains two integers, N and M, denoting the number of rows and columns in the array. The next N lines of each test case contain M space-separated integers denoting the elements of the array arr.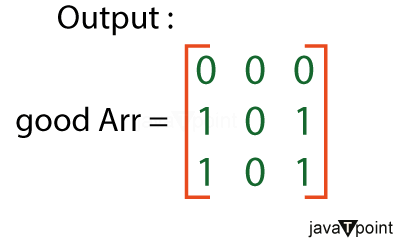

Output Format:

For each test case, return the updated matrix after updating the given matrix as described in the problem statement.

Algorithm

Make a two-dimensional array called "the answer" that has N rows and M columns.
Copy all elements from the matrix arr to the array answer.
Iterate over each element in the matrix arr.
- If the element ARR[row][col] is equal to 0, perform the following:
  - Set all elements in the entire row to 0 by iterating over the index from 0 to N-1 and setting answer[index][col] to 0.
  - Set all elements in the entire column to 0 by iterating over the index from 0 to M-1 and setting answer[row][index] to 0.
Return the matrix answer.
End the program.

Implementation:

Filename: GoodMatrix.java

public class GoodMatrix {
    public static void main(String[] args) {
        int t = 1; // Number of test cases

        for (int testCase = 0; testCase < t; testCase++) {
            int n = 4; // Number of rows
            int m = 4; // Number of columns

            int[][] arr = {
                {1, 1, 1, 1},
                {0, 1, 1, 1},
                {1, 1, 1, 1},
                {1, 1, 1, 0}
            };

            // Convert the matrix to a good matrix
            int[][] goodMatrix = convertToGoodMatrix(arr, n, m);

            // Print the good matrix
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    System.out.print(goodMatrix[i][j] + " ");
                }
                System.out.println();
            }
        }
    }

    public static int[][] convertToGoodMatrix(int[][] arr, int n, int m) {
        int[][] answer = new int[n][m];

        // Copy elements from the given matrix to the answer matrix
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                answer[i][j] = arr[i][j];
            }
        }

        // Iterate over each element in the given matrix
        for (int row = 0; row < n; row++) {
            for (int col = 0; col < m; col++) {
                if (arr[row][col] == 0) {
                    // Set all elements in the entire row to 0
                    for (int index = 0; index < n; index++) {
                        answer[index][col] = 0;
                    }

                    // Set all elements in the entire column to 0
                    for (int index = 0; index < m; index++) {
                        answer[row][index] = 0;
                    }
                }
            }
        }

        return answer;
    }
}

Output:

Complexity Analysis:

Time Complexity: The code iterates over each element in the given matrix, resulting in nested loops. The outer loop iterates 'row' from 0 to 'n - 1', where 'n' is the number of rows. Where'm' is the number of columns, the inner loop iterates 'col' from 0 to'm - 1'. Within the nested loops, there are additional loops for setting the row and column values to 0. As a result, the time complexity is denoted by the notation O(n * m * (n + m)), where n denotes the number of rows and m the number of columns.

Space Complexity: The code creates a new 2-dimensional array 'answer' to store the modified matrix. The space required for the 'answer' array is the same as the input matrix: ' n' rows and 'm' columns. Therefore, the space complexity is O(n * m).

Next TopicHow Streams Work in Java

← prev next →