Heap Implementation in Java

In Java, Heap is a special type of data structure where the root node or parent node is compared with its left and right children and arranged according to the order. Suppose, x is a root node and y is the child node, property key(x)<= key(y) will generate min-heap, and that relation is referred to as "Heap Property".

Based on the order of the parent and child nodes, Heap can be classified in two forms, i.e., Min heap and Max heap. Let's understand both of them one by one and implement the code in Java.

Operations of Heap

Insertion: Add the new element at the end of the heap (array) and then "heapify up" to maintain the heap property by comparing the added element with its parent and swapping if necessary until the correct position is found.

Deletion: Remove the root element (minimum for a min heap, maximum for a max heap), replace it with the last element in the heap, and then "heapify down" by comparing the new root with its children and swapping if necessary until the correct position is found.

Heapify: Adjust the heap to maintain the heap property. In heapify-up, the newly added element is compared with its parent and swapped if needed. In heapify-down, the root element is compared with its children and swapped if needed. This process ensures the heap remains a valid min or max heap.

Min heap

Min heap is a special type of heap data structure that is a complete binary tree in itself. Min heap has the following properties:

Root node value is always smaller in comparison to the other nodes of the heap.
Each internal node has a key value that is always smaller or equal to its children.

We can perform the following three operations in Min heap:

insertNode()

We can perform insertion in the Min heap by adding a new key at the end of the tree. If the value of the inserted key is smaller than its parent node, we have to traverse the key upwards for fulfilling the heap property. The insertion process takes O(log n) time.

extractMin()

It is one of the most important operations which we perform to remove the minimum value node, i.e., the root node of the heap. After removing the root node, we have to make sure that heap property should be maintained. The extractMin() operation takes O(Logn) time to remove the minimum element from the heap.

getMin()

The getMin() operation is used to get the root node of the heap, i.e., minimum element in O(1) time.

Example: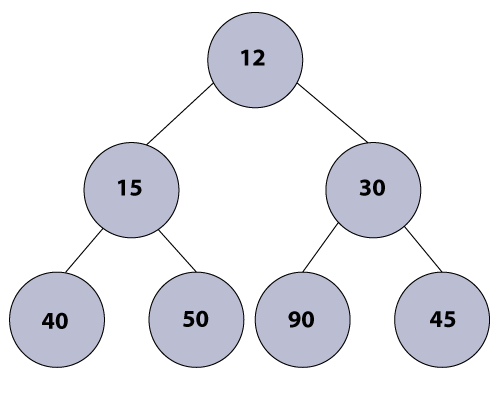

Min heap Algorithm

proceduredesign_min_heap
Array arr: of size n => array of elements
// call min_heapify procedure for each element of the array to form min heap
repeat for (k = n/2 ; k >= 1 ; k--)
	call procedure min_heapify (arr, k);
proceduremin_heapify (vararr[ ] , var k, varn)
{
varleft_child  = 2*k;
varright_child = 2*k+1;
var smallest;
if(left_child<= n and arr[left_child ] <arr[ k ] )
smallest = left_child;
else
smallest = k;
if(right_child<= n and arr[right_child ] <arr[smallest] )
smallest = right_child;
if(smallest != k)
    {
swaparr[ k ] and  arr[ smallest ]);
callmin_heapify (arr, smallest, n);
    } 
}

MinHeapJavaImplementation.java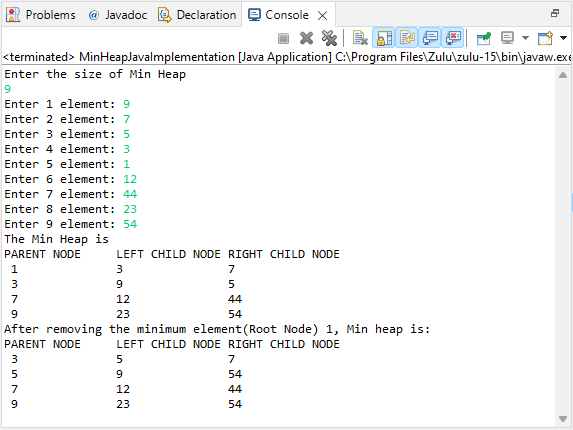

// import required classes and packages
packagejavaTpoint.javacodes;

importjava.util.Scanner;

// create class MinHeap to construct Min heap in Java
classMinHeap { 
	// declare array and variables
privateint[] heapData; 
privateintsizeOfHeap; 
privateintheapMaxSize; 

private static final int FRONT = 1; 
    //use constructor to initialize heapData array
publicMinHeap(intheapMaxSize)  { 
this.heapMaxSize = heapMaxSize; 
this.sizeOfHeap = 0; 
heapData = new int[this.heapMaxSize + 1]; 
heapData[0] = Integer.MIN_VALUE; 
    } 

    // create getParentPos() method that returns parent position for the node 
privateintgetParentPosition(int position)  { 
return position / 2; 
    } 

    // create getLeftChildPosition() method that returns the position of left child 
privateintgetLeftChildPosition(int position)  { 
return (2 * position); 
    } 

    // create getRightChildPosition() method that returns the position of right child
privateintgetRightChildPosition(int position)  { 
return (2 * position) + 1; 
    } 

    // checks whether the given node is leaf or not
privatebooleancheckLeaf(int position)  { 
if (position >= (sizeOfHeap / 2) && position <= sizeOfHeap) { 
return true; 
        } 
return false; 
    } 

    // create swapNodes() method that perform swapping of the given nodes of the heap 
    // firstNode and secondNode are the positions of the nodes
private void swap(intfirstNode, intsecondNode)  { 
int temp; 
temp = heapData[firstNode]; 
heapData[firstNode] = heapData[secondNode]; 
heapData[secondNode] = temp; 
    } 

    // create minHeapify() method to heapify the node for maintaining the heap property
private void minHeapify(int position)  { 

        //check whether the given node is non-leaf and greater than its right and left child
if (!checkLeaf(position)) { 
if (heapData[position] >heapData[getLeftChildPosition(position)] || heapData[position] >heapData[getRightChildPosition(position)]) { 

                // swap with left child and then heapify the left child 
if (heapData[getLeftChildPosition(position)] <heapData[getRightChildPosition(position)]) { 
swap(position, getLeftChildPosition(position)); 
minHeapify(getLeftChildPosition(position)); 
                } 

                // Swap with the right child and heapify the right child 
else { 
swap(position, getRightChildPosition(position)); 
minHeapify(getRightChildPosition(position)); 
                } 
            } 
        } 
    } 

    // create insertNode() method to insert element in the heap
public void insertNode(int data)  { 
if (sizeOfHeap>= heapMaxSize) { 
return; 
        } 
heapData[++sizeOfHeap] = data; 
int current = sizeOfHeap; 

while (heapData[current] <heapData[getParentPosition(current)]) {  
swap(current, getParentPosition(current)); 
current = getParentPosition(current); 
        } 
    } 

    // crreatedisplayHeap() method to print the data of the heap 
public void displayHeap()  { 
System.out.println("PARENT NODE" + "\t" + "LEFT CHILD NODE" + "\t" + "RIGHT CHILD NODE");
for (int k = 1; k <= sizeOfHeap / 2; k++) { 
System.out.print(" " + heapData[k] + "\t\t" + heapData[2 * k] + "\t\t" + heapData[2 * k + 1]); 
System.out.println(); 
        } 
    } 

   // create designMinHeap() method to construct min heap
public void designMinHeap()  { 
for (int position = (sizeOfHeap / 2); position >= 1; position--) { 
minHeapify(position); 
        } 
    } 

    // create removeRoot() method for removing minimum element from the heap
publicintremoveRoot()  { 
intpopElement = heapData[FRONT]; 
heapData[FRONT] = heapData[sizeOfHeap--]; 
minHeapify(FRONT); 
returnpopElement; 
    } 
}

// create MinHeapJavaImplementation class to create heap in Java
classMinHeapJavaImplementation{
	
	// main() method start
public static void main(String[] arg)  { 
	// declare variable
	intheapSize;
	
	// create scanner class object
	Scanner sc = new Scanner(System.in);
	
	System.out.println("Enter the size of Min Heap");
	heapSize = sc.nextInt();
	
	MinHeapheapObj = new MinHeap(heapSize);
	
	for(inti = 1; i<= heapSize; i++) {
		System.out.print("Enter "+i+" element: ");
		int data = sc.nextInt();
		heapObj.insertNode(data);
	}
	
        // close scanner class obj
sc.close();

        //construct a min heap from given data
heapObj.designMinHeap(); 

        //display the min heap data
System.out.println("The Min Heap is "); 
heapObj.displayHeap(); 

        //removing the root node from the heap
System.out.println("After removing the minimum element(Root Node) "+heapObj.removeRoot()+", Min heap is:"); 
heapObj.displayHeap(); 

    } 
}

Output:

Using Arrays

A min heap is a binary tree where the parent node is always smaller than its child nodes, ensuring the smallest element is at the root. Implementing a min heap in Java using an array allows efficient insertion, deletion, and heapification through simple index arithmetic. This structure is ideal for applications requiring quick access to the minimum element, such as priority queues.

File Name: RefactoredMinHeap.java

import java.util.Arrays; // Importing the Arrays class for array manipulation
public class RefactoredMinHeap {
    private int[] heapArray; // Array to store heap elements
    private int currentSize; // Current number of elements in the heap
    private int maxSize; // Maximum capacity of the heap
    // Constructor to initialize the heap with a given capacity
    public RefactoredMinHeap(int maxSize) {
        this.maxSize = maxSize; // Set the maximum size
        this.currentSize = 0; // Initialize current size to 0
        heapArray = new int[maxSize]; // Create a new array of the given capacity
    }
    // Method to get the index of the parent of a given node
    private int getParentIndex(int index) {
        return (index - 1) / 2; // Return the parent index
    }
    // Method to get the index of the left child of a given node
    private int getLeftChildIndex(int index) {
        return (index * 2) + 1; // Return the left child index
    }
    // Method to get the index of the right child of a given node
    private int getRightChildIndex(int index) {
        return (index * 2) + 2; // Return the right child index
    }
    // Method to check if a node is a leaf node
    private boolean isLeafNode(int index) {
        return getRightChildIndex(index) >= currentSize || getLeftChildIndex(index) >= currentSize; // Check if the node is a leaf node
    }
    // Method to insert a new element into the heap
    public void addElement(int element) {
        if (currentSize >= maxSize) { // If the heap is full, return
            return;
        }
        heapArray[currentSize] = element; // Add the new element to the heap
        int currentIndex = currentSize; // Initialize current index
        // Bubble up the new element to maintain heap property
        while (heapArray[currentIndex] < heapArray[getParentIndex(currentIndex)]) {
            swapElements(currentIndex, getParentIndex(currentIndex)); // Swap with parent if smaller
            currentIndex = getParentIndex(currentIndex); // Update current index to parent index
        }
        currentSize++; // Increase the current size of the heap
    }
    // Method to remove and return the minimum element from the heap
    public int removeMin() {
        int minElement = heapArray[0]; // The root element is the minimum element
        heapArray[0] = heapArray[--currentSize]; // Replace the root with the last element
        heapifyDown(0); // Heapify down from the root to maintain heap property
        return minElement; // Return the minimum element
    }
    // Method to heapify down from a given index
    private void heapifyDown(int index) {
        // If the node is not a leaf node
        if (!isLeafNode(index)) {
            // If the current node is greater than either of its children
            if (heapArray[index] > heapArray[getLeftChildIndex(index)] || 
                heapArray[index] > heapArray[getRightChildIndex(index)]) {
                // Swap with the smaller child and heapify down recursively
                if (heapArray[getLeftChildIndex(index)] < heapArray[getRightChildIndex(index)]) {
                    swapElements(index, getLeftChildIndex(index));
                    heapifyDown(getLeftChildIndex(index));
                } else {
                    swapElements(index, getRightChildIndex(index));
                    heapifyDown(getRightChildIndex(index));
                }
            }
        }
    }
    // Method to build a min heap from an arbitrary array
    public void buildMinHeap() {
        // Heapify down from the last non-leaf node to the root
        for (int i = (currentSize / 2) - 1; i >= 0; i--) {
            heapifyDown(i);
        }
    }
    // Method to display the heap elements
    public void displayHeap() {
        // Loop through each parent node and print its children
        for (int i = 0; i < currentSize / 2; i++) {
            System.out.print("Parent : " + heapArray[i]);
            if (getLeftChildIndex(i) < currentSize)
                System.out.print(" Left : " + heapArray[getLeftChildIndex(i)]);
            if (getRightChildIndex(i) < currentSize)
                System.out.print(" Right : " + heapArray[getRightChildIndex(i)]);
            System.out.println();
        }
    }
    // Method to swap two elements in the heap
    private void swapElements(int index1, int index2) {
        int temp = heapArray[index1]; // Temporary variable to hold one element
        heapArray[index1] = heapArray[index2]; // Swap the elements
        heapArray[index2] = temp; // Complete the swap
    }
    // Main method to test the heap implementation
    public static void main(String[] args) {
        RefactoredMinHeap minHeap = new RefactoredMinHeap(7); // Create a new heap of size 7
        minHeap.addElement(3); // Insert element 3
        minHeap.addElement(13); // Insert element 13
        minHeap.addElement(7); // Insert element 7
        minHeap.addElement(16); // Insert element 16
        minHeap.addElement(21); // Insert element 21
        minHeap.addElement(12); // Insert element 12
        minHeap.addElement(9); // Insert element 9
        minHeap.buildMinHeap(); // Build the min heap
        // Display the heap
        System.out.println("The Min Heap is: " + Arrays.toString(minHeap.heapArray));
        minHeap.displayHeap(); // Display the heap elements
        System.out.println("\nThe Min Value is: " + minHeap.removeMin()); // Remove and print the minimum value
        System.out.println("\nThe Min Heap is: " + Arrays.toString(minHeap.heapArray)); // Display the heap after removal
        minHeap.displayHeap(); // Display the heap elements
    }
}

Output:

The Min Heap is: [3, 13, 7, 16, 21, 12, 9]
Parent : 3 Left : 13 Right : 7
Parent : 13 Left : 16 Right : 21
Parent : 7 Left : 12 Right : 9

The Min Value is: 3

The Min Heap is: [7, 13, 9, 16, 21, 12, 9]
Parent : 7 Left : 13 Right : 9
Parent : 13 Left : 16 Right : 21
Parent : 9 Left : 12

Max heap

Max heap is another special type of heap data structure that is also a complete binary tree in itself in Java. Max heap has the following properties:

Root node value is always greater in comparison to the other nodes of the heap.
Each internal node has a key value that is always greater or equal to its children.

We can perform the following three operations in Max heap:

insertNode()

We can perform insertion in the Max heap by adding a new key at the end of the tree. If the value of the inserted key is greater than its parent node, we have to traverse the key upwards for fulfilling the heap property. The insertion process takes O(log n) time.

extractMax()

It is one of the most important operations which we perform to remove the maximum value node, i.e., the root node of the heap. After removing the root node, we have to make sure that heap property should be maintained. The extractMax() operation takes O(Log n) time to remove the maximum element from the heap.

getMax()

The getMax() operation is used to get the root node of the heap, i.e., maximum element in O(1) time.

Example: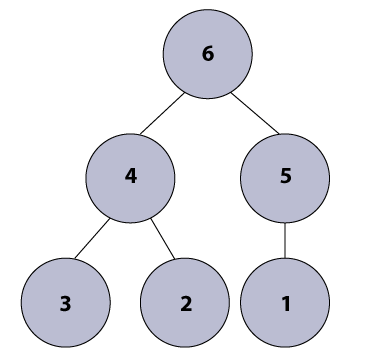

Min heap Algorithm

proceduredesign_max_heap
Array arr: of size n => array of elements
// call min_heapify procedure for each element of the array to form max heap
repeat for (k = n/2 ; k >= 1 ; k--)
	call procedure max_heapify (arr, k);
proceduremin_heapify (vararr[ ] , var k, varn)
{
varleft_child  = 2*k + 1;
varright_child = 2*k+ 2;
if(left_child<= n and arr[left_child] >arr[ largest ] )
largest = left_child;
else
largest = k;
if(right_child<= n and arr[right_child] >arr[largest] )
largest = right_child;
if(largest != k)
    {
swaparr[ k ] and  arr[ largest ]);
callmax_heapify (arr, largest, n);
    } 
}

MaxHeapJavaImplementation.java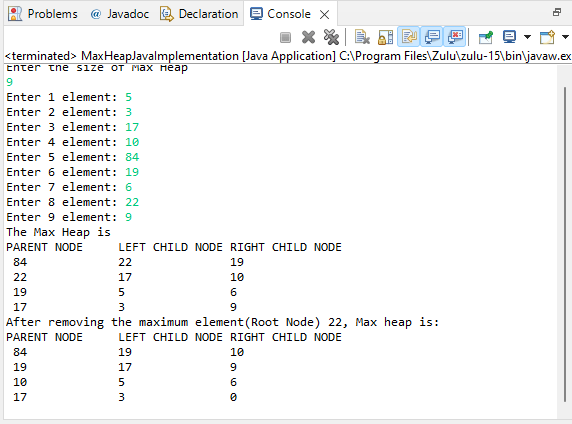

//import required classes and packages
packagejavaTpoint.javacodes;

importjava.util.Scanner;

//create class MinHeap to construct Min heap in Java
classMaxHeap { 
	// declare array and variables
	privateint[] heapData; 
	privateintsizeOfHeap; 
	privateintheapMaxSize; 

	private static final int FRONT = 1; 

	//use constructor to initialize heapData array
	publicMaxHeap(intheapMaxSize)  { 
		this.heapMaxSize = heapMaxSize; 
		this.sizeOfHeap = 0; 
		heapData = new int[this.heapMaxSize];
	} 

	// create getParentPos() method that returns parent position for the node 
	privateintgetParentPosition(int position)  { 
		return (position - 1) / 2; 
	} 

	// create getLeftChildPosition() method that returns the position of left child 
	privateintgetLeftChildPosition(int position)  { 
		return (2 * position); 
	} 

	// create getRightChildPosition() method that returns the position of right child
	privateintgetRightChildPosition(int position)  { 
		return (2 * position) + 1; 
	} 

	// checks whether the given node is leaf or not
	privatebooleancheckLeaf(int position)  { 
		if (position > (sizeOfHeap / 2) && position <= sizeOfHeap) { 
			return true; 
		} 
		return false; 
	} 

	// create swapNodes() method that perform swapping of the given nodes of the heap 
	// firstNode and secondNode are the positions of the nodes
	private void swap(intfirstNode, intsecondNode)  { 
		int temp; 
		temp = heapData[firstNode]; 
		heapData[firstNode] = heapData[secondNode]; 
		heapData[secondNode] = temp; 
	} 

	// create maxHeapify() method to heapify the node for maintaining the heap property
	private void maxHeapify(int position)  { 

	     //check whether the given node is non-leaf and greater than its right and left child
	if (!checkLeaf(position)) { 
	if (heapData[position] <heapData[getLeftChildPosition(position)] || heapData[position] <heapData[getRightChildPosition(position)]) { 
	
	             // swap with left child and then heapify the left child 
	if (heapData[getLeftChildPosition(position)] >heapData[getRightChildPosition(position)]) { 
	swap(position, getLeftChildPosition(position)); 
	maxHeapify(getLeftChildPosition(position)); 
	             } 
	
	             // Swap with the right child and heapify the right child 
	else { 
	swap(position, getRightChildPosition(position)); 
	maxHeapify(getRightChildPosition(position)); 
	             } 
	         } 
	     } 
	} 

	// create insertNode() method to insert element in the heap
	public void insertNode(int data)  { 
		heapData[sizeOfHeap] = data; 
		int current = sizeOfHeap; 

		while (heapData[current] >heapData[getParentPosition(current)]) {  
			swap(current, getParentPosition(current)); 
			current = getParentPosition(current); 
		} 
		sizeOfHeap++;
	} 

	// create displayHeap() method to print the data of the heap 
	public void displayHeap()  { 
		System.out.println("PARENT NODE" + "\t" + "LEFT CHILD NODE" + "\t" + "RIGHT CHILD NODE");
		for (int k = 0; k <sizeOfHeap / 2; k++) { 
			System.out.print(" " + heapData[k] + "\t\t" + heapData[2 * k + 1] + "\t\t" + heapData[2 * k + 2]); 
			System.out.println(); 
		} 
	} 

	// create designMaxHeap() method to construct min heap
	public void designMaxHeap()  { 
		for (int position = 0;  position < (sizeOfHeap / 2); position++) { 
			maxHeapify(position); 
		} 
	} 

	// create removeRoot() method for removing maximum element from the heap
	publicintremoveRoot()  { 
		intpopElement = heapData[FRONT]; 
		heapData[FRONT] = heapData[sizeOfHeap--]; 
		maxHeapify(FRONT); 
		returnpopElement; 
	} 
}

//create MinHeapJavaImplementation class to create heap in Java
classMaxHeapJavaImplementation{
	
	// main() method start
public static void main(String[] arg)  { 
	// declare variable
	intheapSize;
	
	// create scanner class object
	Scanner sc = new Scanner(System.in);
	
	System.out.println("Enter the size of Max Heap");
	heapSize = sc.nextInt();
	
	MaxHeapheapObj = new MaxHeap(50);
	
	for(inti = 1; i<= heapSize; i++) {
		System.out.print("Enter "+i+" element: ");
		int data = sc.nextInt();
		heapObj.insertNode(data);
	}
	
     // close scanner class obj
sc.close();

     //construct a max heap from given data
heapObj.designMaxHeap(); 

     //display the max heap data
System.out.println("The Max Heap is "); 
heapObj.displayHeap(); 

     //removing the root node from the heap
System.out.println("After removing the maximum element(Root Node) "+heapObj.removeRoot()+", Max heap is:"); 
heapObj.displayHeap(); 

 } 
}

Output:

Using Collections.reverseOrder() method via library Functions

The Collections.reverseOrder() method in Java is a powerful utility for reversing the natural ordering of elements in a collection. This method returns a comparator that imposes the reverse of the natural ordering on a collection of objects that implement the Comparable interface. By leveraging this method, developers can easily transform a min-heap into a max-heap, reverse the order of a sorted list, or adjust the priority of elements in a priority queue.

File Name: MaxHeapDemo.java

// Java program to demonstrate working
// of PriorityQueue as a Max Heap
// Using Collections.reverseOrder() method
// Importing necessary classes
import java.util.*;
// Main class
class MaxHeapDemo {
    // Main method
    public static void main(String args[]) {
        // Creating empty priority queue
        PriorityQueue<Integer> maxHeap
                = new PriorityQueue<Integer>(
                        Collections.reverseOrder());
        // Adding items to our priority queue
        // using add() method
        maxHeap.add(10);
        maxHeap.add(30);
        maxHeap.add(20);
        maxHeap.add(400);
        // Printing the most priority element
        System.out.println("Head value using peek function:"
                + maxHeap.peek());
        // Printing all elements
        System.out.println("The queue elements:");
        Iterator<Integer> iterator = maxHeap.iterator();
        while (iterator.hasNext())
            System.out.println(iterator.next());
        // Removing the top priority element (or head) and
        // printing the modified maxHeap using poll()
        maxHeap.poll();
        System.out.println("After removing an element "
                + "with poll function:");
        Iterator<Integer> iterator2 = maxHeap.iterator();
        while (iterator2.hasNext())
            System.out.println(iterator2.next());
        // Removing 30 using remove() method
        maxHeap.remove(30);
        System.out.println("After removing 30 with"
                + " remove function:");
        Iterator<Integer> iterator3 = maxHeap.iterator();
        while (iterator3.hasNext())
            System.out.println(iterator3.next());
        // Check if an element is present using contains()
        boolean contains20 = maxHeap.contains(20);
        System.out.println("Priority queue contains 20 "
                + "or not?: " + contains20);
        // Getting objects from the queue using toArray()
        // in an array and print the array
        Object[] array = maxHeap.toArray();
        System.out.println("Values in array: ");
        for (int i = 0; i < array.length; i++)
            System.out.println("Value: "
                    + array[i].toString());
    }
}

Output:

Head value using peek function:400
The queue elements:
400
30
20
10
After removing an element with poll function:
30
10
20
After removing 30 with remove function:
20
10
Priority queue contains 20 or not?: true
Values in array: 
Value: 20
Value: 10

Applications of Heap

Priority Queues: Heaps are commonly utilized to implement priority queues, where elements with higher priority are extracted first. This is essential in applications such as task scheduling, interrupt handling, and event processing.

Sorting Algorithms: Heapsort, a comparison-based sorting algorithm, relies on the Heap data structure. It offers a time complexity of O(n log n), making it efficient for sorting large datasets.

Graph Algorithms: Heaps are integral in graph algorithms like Dijkstra's shortest path algorithm, Prim's minimum spanning tree algorithm, and the A* search algorithm.

File Compression: Heaps play a crucial role in data compression techniques such as Huffman coding. Here, a priority queue, typically implemented as a min-heap, constructs a Huffman tree.

Dynamic Programming: Heaps are employed in dynamic programming algorithms, particularly in greedy algorithms where elements are processed based on their priority.

Medical Applications: In medical settings, heaps are used to manage patient information, including vital signs, treatments, and test results, based on their criticality or urgency.

External Sorting: Heaps are employed in external sorting algorithms to efficiently sort large datasets that exceed memory capacity. Chunks of data are processed using a priority queue.

Load Balancing: Heaps are applied in load balancing algorithms to distribute tasks or requests among servers. Tasks are typically processed according to their priority or load.

Online Algorithms: Heaps find application in online algorithms that process data in real-time as it arrives, such as in recommendation systems, event processing, and streaming data management.

Financial Applications: Heaps are utilized in financial applications such as stock market analysis and algorithmic trading, where they manage and process stock data based on priority.

Advantages of Heap

Efficient Insertion and Deletion: The heap structure supports efficient insertion and deletion of elements. When a new element is inserted, it is initially placed at the end of the heap and then moved to its correct position using the heapify operation. Similarly, when an element is removed, it is replaced by the last element in the heap, and the heap is restructured using the heapify operation.

Efficient Priority Queue Implementation: Heaps are commonly used to implement priority queues, where the highest priority element is always located at the top of the heap. This allows for constant-time access to the highest priority element, making heaps a highly efficient data structure for priority queue implementations.

Guaranteed Access to Extreme Values: In a max-heap, the maximum element is always at the root, while in a min-heap, the minimum element is always at the root. This property ensures that the heap provides guaranteed access to the maximum or minimum element, which is useful in algorithms requiring quick access to extreme values.

Space Efficiency: The heap structure is space-efficient as it organizes elements in a complete binary tree, which typically uses less memory compared to other data structures like linked lists or dynamic arrays.

Heap Sort Algorithm: The heap data structure is the foundation of the heap sort algorithm, an efficient sorting method with a worst-case time complexity of O(n log n). This makes heap sort a robust choice for sorting large datasets.

Disadvantages of Heap

Lack of Flexibility: The heap structure is designed to maintain a specific order of elements, which limits its flexibility. This makes it less suitable for applications that require more adaptable data structures.

Inefficient for Searching: While heaps provide efficient access to the top element, they are not ideal for searching for specific elements. Finding an element in a heap involves traversing the entire tree, resulting in a time complexity of O(n).

Instability: Heaps are not stable data structures, meaning that the relative order of elements with equal values may not be preserved during insertion or modification.

Memory Management Challenges: Heaps require dynamic memory allocation, which can be problematic in systems with limited memory resources. Additionally, managing the allocated memory for heaps can be complex and prone to errors.

Complexity Considerations: Although heaps allow efficient insertion, deletion, and priority queue operations, the worst-case time complexity is O(n log n). This may not be optimal for applications that need faster algorithms.

Next TopicHow to Check null in Java

← prev next →