Hill Cipher Program in JavaIn classical cryptography, the hill cipher is a polygraphic substitution cipher based on Linear Algebra. It was invented by Lester S. Hill in the year 1929. In simple words, it is a cryptography algorithm used to encrypt and decrypt data for the purpose of data security. The algorithm uses matrix calculations used in Linear Algebra. It is easier to understand if we have the basic knowledge of matrix multiplication, modulo calculation, and the inverse calculation of matrices. In hill cipher algorithm every letter (A-Z) is represented by a number moduli 26. Usually, the simple substitution scheme is used where A = 0, B = 1, C = 2…Z = 25 in order to use 2x2 key matrix. Note: The complexity of the algorithm increases with the size of the key matrix.EncryptionTo encrypt the text using hill cipher, we need to perform the following operation. Where K is the key matrix and P is plain text in vector form. Matrix multiplication of K and P generates the encrypted ciphertext. Steps For EncryptionStep 1: Let's say our key text (2x2) is DCDF. Convert this key using a substitution scheme into a 2x2 key matrix as shown below: 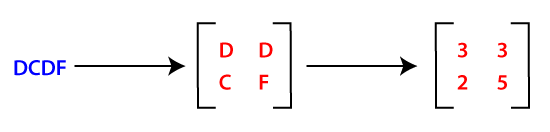
Step 2: Now, we will convert our plain text into vector form. Since the key matrix is 2x2, the vector must be 2x1 for matrix multiplication. (Suppose the key matrix is 3x3, a vector will be a 3x1 matrix.) In our case, plain text is TEXT that is four letters long word; thus we can put in a 2x1 vector and then substitute as: 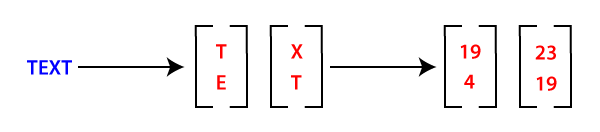
Step 3: Multiply the key matrix with each 2x1 plain text vector, and take the modulo of result (2x1 vectors) by 26. Then concatenate the results, and we get the encrypted or ciphertext as RGWL. 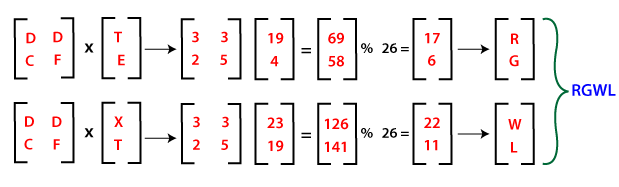
DecryptionTo encrypt the text using hill cipher, we need to perform the following operation. Where K is the key matrix and C is the ciphertext in vector form. Matrix multiplication of inverse of key matrix K and ciphertext C generates the decrypted plain text. Steps For DecryptionStep 1: Calculate the inverse of the key matrix. First, we need to find the determinant of the key matrix (must be between 0-25). Here the Extended Euclidean algorithm is used to get modulo multiplicative inverse of key matrix determinant 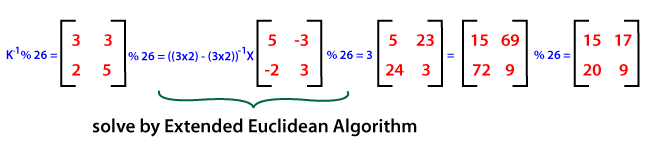
Step 2: Now, we multiply the 2x1 blocks of ciphertext and the inverse of the key matrix. The resultant block after concatenation is the plain text that we have encrypted i.e., TEXT. 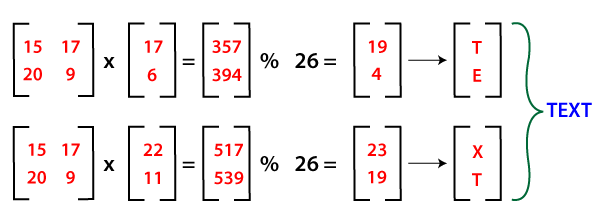
Let's see an example. Consider the following program in which we have performed the hill cipher encryption and decrpytion on a 2 x 2 matrix. Here, we follow both the substitution schemes, A = 0, B = 1,… and A = 1, B = 2,… HillCipherExample.java Output: 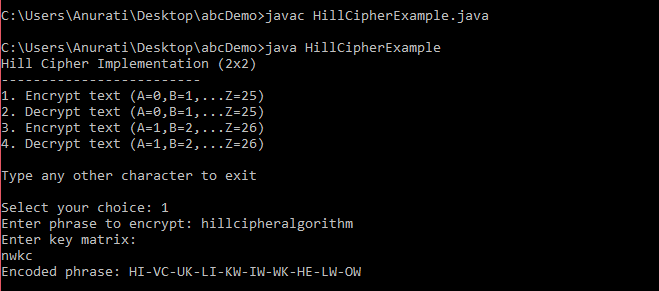
Next TopicLazy Loading in Java
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










